Caesar Cipher (2020 China Collegiate Programming Contest, Weihai Site)
题目来源
https://codeforces.ml/gym/102798
题意分析
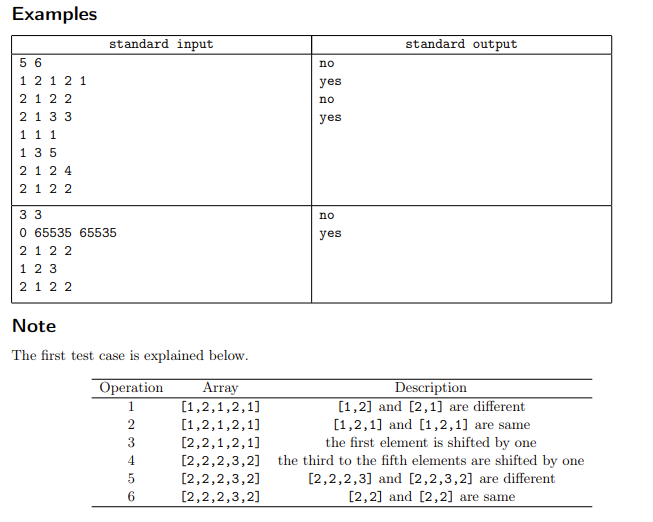
题目意思的大致可以描述为，给一个长度为n的序列，有两次操作。操作1是将某一区间段的数全部加1，操作2是询问以某两个位置x，y为起点的长度为ln的序列是否相同,进行yes\no的输出。需要注意的是，区间中的所有数字都在[0,65535)这个区间之内。
思路分析
由操作1想到的是线段树。由操作2想到的是hash。用线段树维护区间的最大值，哈希值和哈希基数值。然后对于操作1来说，就是一个区间修改+区间判断修改（即判断是否出现越界情况）。操作2就是一个区间查询。
说的很容易，然而还是被这道题上了一课。
code
1 #include <bits/stdc++.h> 2 3 #define int long long 4 using namespace std; 5 const int maxn = 5e5 + 7; 6 const int pp = 13331; 7 const int mod = 1e9 + 7; 8 const int MOD = 65536; 9 10 int a[maxn]; 11 int tree[maxn << 2], ver[maxn << 2], lz[maxn << 2]; 12 int base[maxn << 2], ps[maxn << 2]; 13 14 void init(){ 15 base[0] = 1; 16 for (int i=1; i<maxn; i++) base[i] = base[i-1] * pp % mod; 17 } 18 19 void pushdown(int p){ 20 if (lz[p]){ 21 lz[p << 1] += lz[p]; 22 lz[p << 1 | 1] += lz[p]; 23 ver[p << 1] = (ver[p << 1] + ps[p << 1] * lz[p]) % mod; 24 ver[p << 1 | 1] = (ver[p << 1 | 1] + ps[p << 1 | 1] * lz[p]) % mod; 25 tree[p << 1] += lz[p]; 26 tree[p << 1 | 1] += lz[p]; 27 lz[p] = 0; 28 } 29 } 30 31 void build(int p, int l, int r){ 32 if (l == r){ 33 tree[p] = a[l]; ver[p] = (base[l] * a[l]) % mod; ps[p] = base[l]; 34 // cout << "P: " << p << " " << tree[p] << " " << ver[p] << " " << ps[p] << endl; 35 return; 36 } 37 int mid = l + r >> 1; 38 build(p << 1, l, mid); 39 build(p << 1 | 1, mid + 1, r); 40 tree[p] = max(tree[p << 1], tree[p << 1 | 1]); 41 ps[p] = (ps[p << 1] + ps[p << 1 | 1]) % mod; 42 ver[p] = (ver[p << 1] + ver[p << 1 | 1]) % mod; 43 // cout << "P: " << p << " " << tree[p] << " " << ver[p] << " " << ps[p] << endl; 44 } 45 46 void update(int p, int l, int r, int L, int R, int x){ 47 if (L <= l && r <= R){ 48 lz[p] += x; tree[p] += x; ver[p] = (ver[p] + ps[p]) % mod; 49 return; 50 } 51 52 int mid = l + r >> 1; 53 pushdown(p); 54 if (L <= mid) update(p << 1, l, mid, L, R, x); 55 if (mid < R) update(p << 1 | 1, mid + 1, r, L, R, x); 56 tree[p] = max(tree[p << 1], tree[p << 1 | 1]); 57 ver[p] = (ver[p << 1] + ver[p << 1 | 1]) % mod; 58 } 59 60 void umod(int p, int l, int r){ 61 // cout << p << " " << tree[p] << " " << l << " " << r << " %%%%\n"; 62 if (tree[p] < MOD) return; 63 if (l == r){ 64 tree[p] = 0; 65 ver[p] = 0; lz[p] = 0; 66 return; 67 } 68 pushdown(p); 69 int mid = l + r >> 1; 70 umod(p << 1, l, mid); 71 umod(p << 1 | 1, mid + 1, r); 72 tree[p] = max(tree[p << 1], tree[p << 1 | 1]); 73 ver[p] = (ver[p << 1] + ver[p << 1 | 1]) % mod; 74 } 75 76 int ask(int p, int l, int r, int L, int R){ 77 if (L <= l && r <= R) { 78 // cout << "p" << p <<endl; 79 return ver[p]; 80 } 81 int mid = l + r >> 1; 82 pushdown(p); 83 int ans = 0; 84 if (L <= mid) ans += ask(p << 1, l, mid, L, R); 85 ans %= mod; 86 if (mid < R) ans += ask(p << 1 | 1, mid + 1, r, L, R); 87 ans %= mod; 88 return ans; 89 } 90 91 signed main(){ 92 init(); 93 int n, q; scanf("%lld%lld", &n, &q); 94 for (int i=1; i<=n; i++) scanf("%lld", &a[i]); 95 build(1, 1, n); 96 97 98 99 while (q --){ 100 int op; scanf("%lld", &op); 101 if (op == 1){ 102 int l, r; scanf("%lld%lld", &l, &r); 103 update(1, 1, n, l, r, 1); 104 umod(1, 1, n); 105 106 // cout << ask(1, 1, n, 1, 1) << " " << ask(1, 1, n, 2, 2) << " " << ask(1, 1, n, 3, 3) << endl; 107 108 }else { 109 int x, y, ln; 110 scanf("%lld%lld%lld", &x, &y, &ln); 111 if (x > y) swap(x, y); 112 int ans1 = ask(1, 1, n, x, x + ln - 1); 113 // cout << "&&&&&&" << endl; 114 // cout << x << " " << x+ln << endl; 115 int ans2 = ask(1, 1, n, y, y + ln - 1); 116 // cout << "ans1: " << ans1 << endl; 117 ans1 = ans1 * base[y-x] % mod; 118 // cout << "ans1: " << ans1 << " ans2: " << ans2 << endl; 119 if (ans1 == ans2) printf("yes\n"); 120 else printf("no\n"); 121 } 122 } 123 return 0; 124 } 125 /* 126 5 1 127 1 2 1 2 1 128 2 1 3 3 129 130 3 2 131 0 65535 65535 132 1 2 3 133 2 1 2 2 134 */
