F. Zero Remainder Sum(Codeforces Round #677 (Div. 3))

题目来源

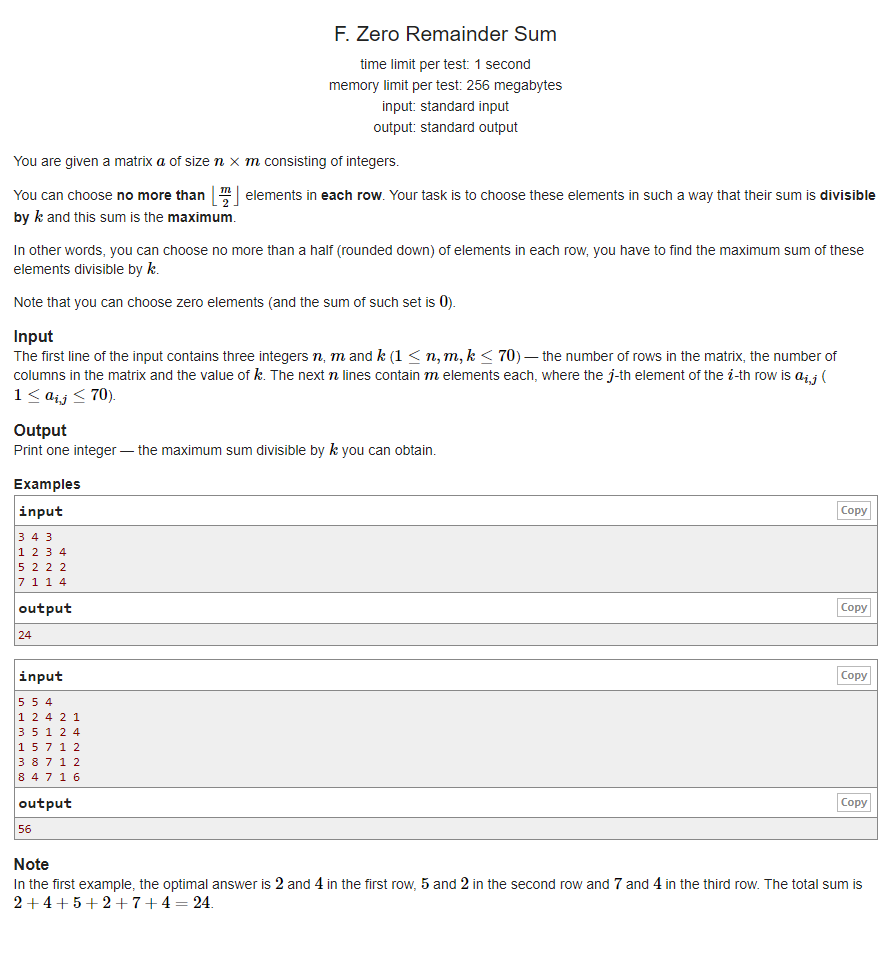
https://codeforces.ml/contest/1433/problem/F

题意分析

　　题目意思的大致可以描述为，给一个n*m的方阵，并且给一个k，每一行我们最多只能取m/2个数字，问在这个方阵之中，在我们取的所有数的和为k的倍数的情况下，这个数和最大是多少？

思路分析

　　数据范围不大，想到dp。
　　首先对每一行进行处理，因为每一行都是独立的。我们要处理出余数从0 - k-1的数的和的最大值，所以开一个数组pre。又因为每一行有长度的限制，所以我们就加一维来规范我们取的长度。所有pre是一个三维的数组，pre[i][j][l]表示的是第i行我们取了l个数，此时的数和对k的余数为j的最大值，这个数组我们可以用一个四重的循环进行初始化。分别循环他的行数，每行数字的个数，长度以及余数。循环长度的时候一定要逆着走，这里应该与01背包中的原理是相同的，即保证每一个数只会被选择一次。
　　那么根据上面的初始化，我们再将上面的数据映射到我们的dp数组之中。因为我们的dp数组表示的是第i行余数为j的最大值，所以要将长度那一维去掉。于是用一个两重循环初始化dp数组，求所有长度下某个余数的最大值。
　　在dp数组被初始化之后，接下来将行与行之间的关系进行处理。即用一个k*k的循环，处理出在两行中取数字时候的各个余数的最大值。那么这样一直处理到第n行，ans[n][0]即是我们最终的答案。
　　最后要提的是要注意所有数组的初始化，具体细节请见代码，其目的是为了排除一些不会出现的情况，不让其对最终答案产生影响。

code

#include <bits/stdc++.h>

#define INF 0x3f3f3f3f
#define ll long long
using namespace std;
const int maxn = 105;

int pre[maxn][maxn][maxn];
int dp[maxn][maxn];
int ans[maxn][maxn];
int a[maxn][maxn];
int n, m, k;

signed main(){
    scanf("%d%d%d", &n, &m, &k);
    for (int i=1; i<=n; i++){
        for (int j=1; j<=m; j++) scanf("%d", &a[i][j]);
    }
    memset(pre, -INF, sizeof (pre));
    for (int i=1; i<=n; i++) pre[i][0][0] = 0;

    for (int i=1; i<=n; i++){
        int ln = m / 2;
        for (int p=1; p<=m; p++){
            for (int l=min(ln, p)-1; l>=0; l--){
                for (int j=0; j<k; j++){
                    int tmp = a[i][p];
                    pre[i][(j+tmp) % k][l+1] = max(pre[i][(j+tmp) % k][l+1], pre[i][j][l] + a[i][p]);
//                    cout << i << " " << (j + tmp) % k << " " << l + 1 << "  " << pre[i][(j+tmp) % k][l+1] << endl;
                }
            }
        }
    }
    memset(dp, -INF, sizeof (dp));
    for (int i=1; i<=n; i++){
        for (int j=0; j<k; j++){
            for (int l=0; l<=m/2; l++){
                dp[i][j] = max(dp[i][j], pre[i][j][l]);
            }
        }
    }

//    for (int i=0; i<k; i++){
//        for (int j=0; j<=m/2; j++) printf("%d ", pre[1][i][j]);
//        printf("\n");
//    }
//    printf("---------------------------\n");
//    for (int i=1; i<=n; i++){
//        for (int j=0; j<k; j++)  printf("%d ", dp[i][j]);
//        printf("\n");
//    }
//    printf("\n");
    memset(ans, -INF, sizeof (ans));
    for (int i=0; i<k; i++) ans[1][i] = dp[1][i];


    for (int i=2; i<=n; i++){
        for (int j=0; j<k; j++){
            for (int p=0; p<k; p++){
                int tmp = (j + p) % k;
                ans[i][tmp] = max(ans[i][tmp], ans[i-1][j] + dp[i][p]);
            }
        }
    }

//    for (int i=2; i<=n; i++){
//        for (int j=0; j<k; j++) printf("%d ", ans[i][j]);
//        printf("\n");
//    }

    printf("%d\n", ans[n][0]);


    return 0;
}