算法与数据结构
算法与数据结构
算法
1、排序算法
- 冒泡排序
- 选择排序
- 插入排序
- 快速排序
- 希尔排序
- 计数排序
2、列表查找
从列表中查找指定的元素
- 顺序查找
从列表第一个元素开始，顺序进行搜索，直到找到为止
- 二分查找
从有序列表的候选区data[0: n]开始，通过对待查找的值与候选区中的值比较使候选区的值减半
1. 算法的衡量标准
1. 时间复杂度
时间复杂度：程序执行的大概次数，使用O（）来计
logn == log2^n
如何一眼判断时间复杂度：
1. 循环减半的过程 ==》O(logn)
2. 几次循环就是n的几次方的复杂度
2. 空间复杂度
用来评估算法内存占用大小的一个式子
2. 冒泡排序
首先列表每相邻两个数进行比较，如果前面的比后面的大，就交换两个数
# 冒泡排序 # 时间复杂度：O(n^2) def bubble_sort(li): for i in range(len(li) - 1): # 趟数 flag = True for j in range(len(li) - 1 - i): # 每一趟内层循环，每一趟确定一个比较次数-i if li[j] > li[j + 1]: # 前面大于后面交换位置 li[j], li[j + 1] = li[j + 1], li[j] flag = False if flag: # 优化：如果一趟循环下来都没有要比较交换的位置说明原本就是顺序的，直接返回 return
3. 选择排序
先选择一个数，默认该数是最小的放在第一的位置，然后再一次遍历取出所有的数与第一个数比较，如果比他大交换位置
# 选择排序 # 时间复杂度：O(n^2) def select_sort(li): for i in range(len(li)): # 将取出的第一个默认是最小的 minloc = i for j in range(i + 1, len(li)): # 循环比较后面的所有值与 第一个元素比较 if li[minloc] > li[j]: # 如果比第一个元素小就换位置 li[minloc], li[j] = li[j], li[minloc]
4. 插入排序
列表被分为有序区域无序区两个部分，最初有序区就一个元素，每次从无序区取出一个元素，插入到有序区的位置，直到无序区变空
# 插入排序 # 时间复杂度：O(n^2) def insert_sort(li): # 将第一个元素作为有序区第一个元素 for i in range(1, len(li)): # 将无序区中的元素取出拿一个变量存着 tmp = li[i] # 获取取去的前一个元素的索引 j = i - 1 # 比较取出的元素与前面的所有元素 while j >= 0 and li[j] > tmp: # 前面的值覆盖取出的值 li[j + 1] = li[j] # 依次循环前面的所有值 j = j - 1 # 比较完j=-1跳出循环，将取出的值作为第一个 li[j + 1] = tmp
5. 快速排序
取一个元素p（第一个元素），使p其归位，列表被p分为两部分，左边的都比p小，右边的比p大，最后递归完成排序
# 快速排序 # 时间复杂度：O(nlogn) def quick_sort(li, left, right): # left与right是左右两边的索引 if left < right: # 调用归为函数得到中间的索引 mid = partition(li, left, right) # 递归减半左右两边 quick_sort(li, left, mid-1) quick_sort(li, mid+1, right) # 归为函数 def partition(li, left, right): # 将第一个元素取出 tem = li[left] while left < right: # 判断右边的是否比取出的第一个元素大，如果大指针移动一位 while left < right and li[right] >= tem: right = right - 1 # 如果右边的比第一个小，将该元素赋值给左边 li[left] = li[right] # 判断左边的元素是否比取出的元素小，如果小指针移动一位 while left < right and li[left] <= tem: left = left + 1 # 如果左边的比取出的大，将该元素赋值给刚右边元素的位置 li[right] = li[left] # 当指针重合时，将取出的第一个元素放下在中间 li[left] = tem mid = left # 或者等于right，两边指针重合时 return mid # quick_sort(li, 0, len(li)-1)
6. 希尔排序
1、希尔排序是一种分组插入排序的算法
2、首先取一个整数d1 = n/2，将元素分为d1个组，每组相邻元素之间距离为d1，在各组内进行直接插入排序
3、再取第二个整数重复上述分组过程，直到di = 1，所有元素在用一个组内进行直接插入排序
4、希尔排序每一趟只是让元素接近有序，最后一趟使所有元素有序
时间复杂度：O(1.3n)
7. 计数排序
时间复杂度：O(n)
def count_sort(li): # 先生成比列表多一个的列表全是0 count = [0 for i in range(len(li)+1)] # 将列表循环取出对应的count=1 print(count) for i in li: count[i] += 1 print(count) # 将原列表清空后再添加 li.clear() # 枚举出count for k, v in enumerate(count): print(k, v) # 去除0和保证重复的数在里面 for i in range(v): li.append(k)
8. 二分查找
时间复杂度：O(logn)
def bin_search(li, value, low, high): if low <= high: mid = (low + high) // 2 if li[mid] == value: return mid elif li[mid] > value: return bin_search(li, value, low, mid-1) else: return bin_search(li, value, mid+1, high) else: return
数据结构
1、线性结构
就是能够用一根线串起来的数据结构
- 数组（列表）
1、申请数组的前提条件是：内存是连续的
2、int a[7] ：代表声明一个数组是a，数组大小是7，数组的元素都是整型
一个数长度是4个字节所以7个是28个字节
3、如何申请内存：在C, C++ 语言中，mallco(28）申请28个字节，用完后要释放: free(28）
4、如果 int a[7] = [1, 2, 3, 4, 5, 6, 7] 那如何知道 a[3] = 4的？
a[3] = 首地址(1000) + 索引(3) * 长度(4）= 1012--1015
5、首地址是保存在数组名中的
- 链表（约瑟夫问题、丢手绢问题）
数组要一块连续的内存空间来存储，对内存的要求比较高。如果我们申请一个 100MB 大小的数组，当内存中没有连续的、足够大的存储空间时，即便内存的剩余总可用空间大于 100MB，仍然会申请失败。 而链表恰恰相反，它并不需要一块连续的内存空间,它通过“指针”将一组零散的内存块串联起来使用，所以如果我们申请的是 100MB 大小的链表，根本不会有问题。
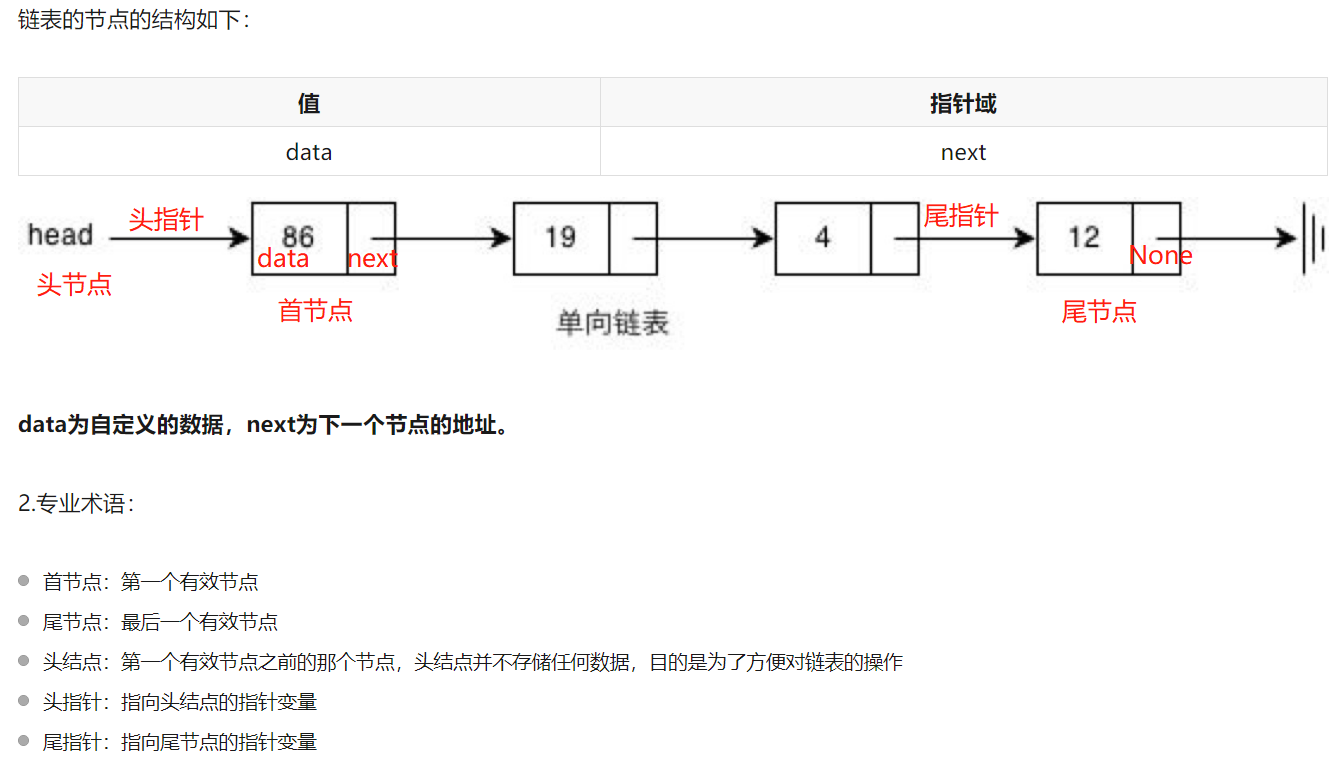
3. 链表分类：
- 单链表
- 双链表，每一个节点有两个指针域
- 循环链表 ，能通过任何一个节点找到其他所有的节点
- 非循环链表
- 每一个节点有两个指针域
- 循环链表 能通过任何一个节点找到其他所有的节点
- 非循环链表
- 线性结构的应用
- 队列
- 栈
2、非线性结构
- 树
- 一般树：任意一个节点的子节点的个数不受限制
- B+树
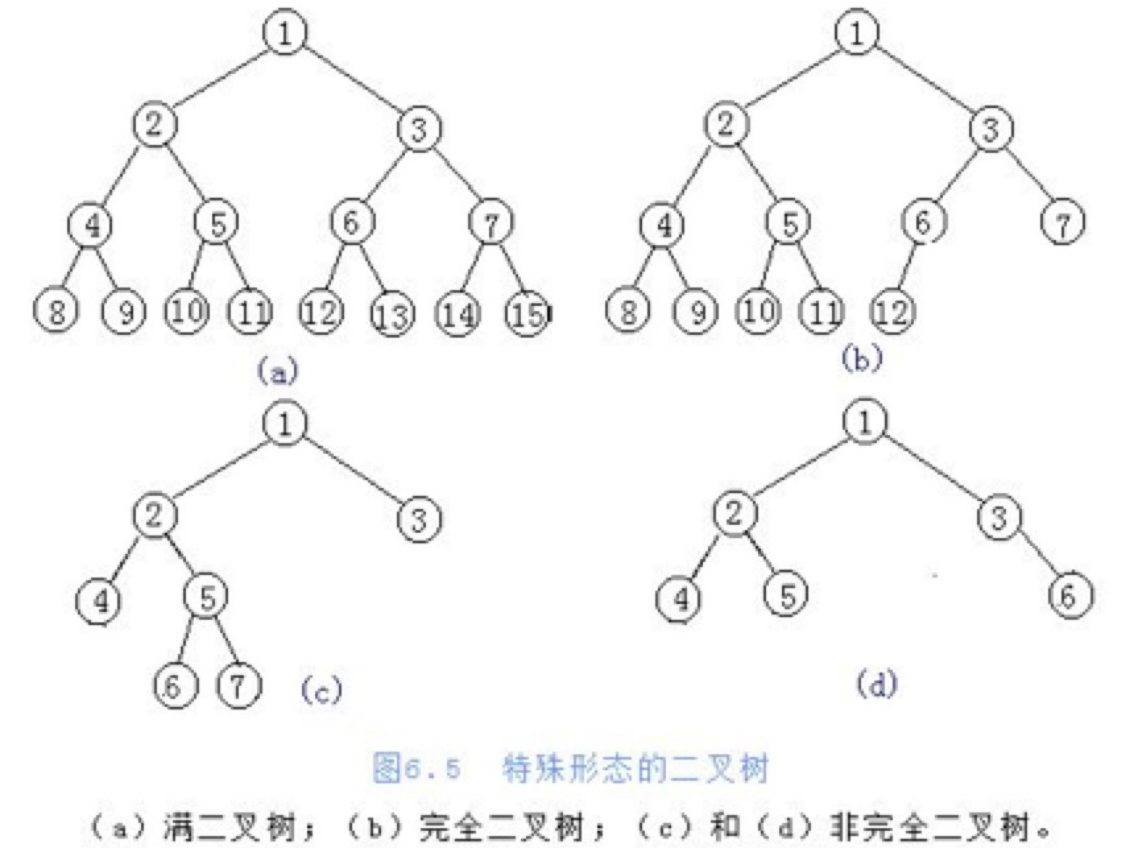
- 二叉树：任意一个节点的子节点的个数最多是两个，且子节点的位置不可更改
- 完全二叉树：只是删除了满二叉树最底层最右边连续的若干个节点
- 满二叉树：在不增加层数的前提下，无法再多添加一个节点的二叉树
- 森林：n个互不相交的数的集合
- mysql的索引：B+树
- 一般树：任意一个节点的子节点的个数不受限制
- 图
