函数(四)
内容概要
-
- 有参装饰器
-
-
算法之二分法
多层装饰器
"""语法糖会将紧挨着的被装饰对象的名字当做参数自动传入装饰器函数中""" # 判断七句print执行顺序 def outter1(func1): print('加载了outter1') def wrapper1(*args, **kwargs): print('执行了wrapper1') res1 = func1(*args, **kwargs) return res1 return wrapper1 def outter2(func2): print('加载了outter2') def wrapper2(*args, **kwargs): print('执行了wrapper2') res2 = func2(*args, **kwargs) return res2 return wrapper2 def outter3(func3): print('加载了outter3') def wrapper3(*args, **kwargs): print('执行了wrapper3') res3 = func3(*args, **kwargs) return res3 return wrapper3 @outter1 @outter2 @outter3 def index(): print('from index')
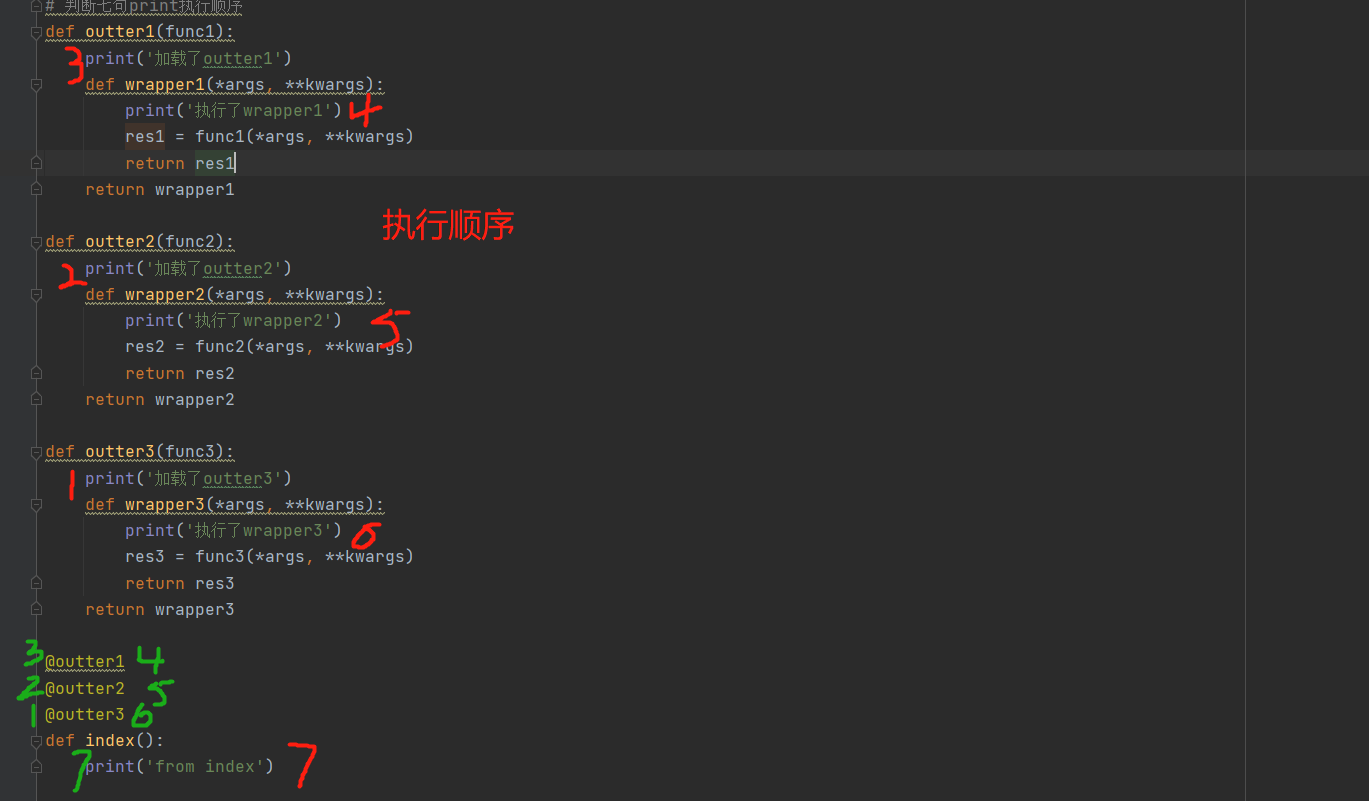
有参装饰器
def outer(source_data): # 只能再套一层函数来当作里层装饰器的参数 最终的有参装饰器完整结构 def login_auth(func_name): # 只能写默认参数但无意义 基本上不能加参数 只能接收一个被装饰对象名字 def inner(*args, **kwargs): # 不能动 是专门用来给被装饰的对象传参的 username = input('username>>>:').strip() password = input('password>>>:').strip() # 校验用户数据 数据的来源可以有很多 比如全局字典 全局列表 文本文件 数据库 # 数据的来源不同 处理方式就不同 对应的代码编写就不一样 # 分支结构处理 然后根据不同的参数提示 匹配不同的流程 if source_data == '1': print('使用字典的方式处理数据') elif source_data == '2': print('使用列表的方式处理数据') elif source_data == '3': print('使用文件操作处理数据') else: print('其他操作情况') res = func_name(*args, **kwargs) return res return inner return login_auth @outer('3') # 函数名加括号 执行优先级最高 def index(): print('from index')
递归函数
本质:递归函数也称为函数的递归
函数在运行过程中直接或者间接的调用了自身
基本演示
# 直接调用自己 def index(): print('from index') index() index() # 会报错 # 类似的间接调用也是如此 ''' 这个类似于while的死循环 会一直自己调用自己 maximum recursion depth exceeded while calling a Python object 最大递归深度超出限制了 python解释器自带的应急机制 在有些编程语言中 甚至没有遇警机制 代码执行真的一致到计算机崩溃为止 这就是python最大递归深度 回答997 998 1000都可以 官方给出的是1000 ''' """ 函数的递归不应该是无限循环的过程 真正的递归函数应该要满足两个要求 1.每次递归 复杂度必须降低(下一次递归要比上一次递归解答) 简单的说 越往下递归应该离解决问题的答案越近 2.必须要有明确的结束条件 """ # 举例诠释 """ 需求:我想知道我们班坐在第一排的某个学生年龄 过程: 我问他多大了 他调皮不告诉我 说比后面那个同学大两岁 后面的说比他后面的大两岁 ... 问到最后你一排 终于开口说 18岁 ... 知道最后一排的年级回推就可以知道第一排的年级 名词: 递推:一层层往下问 回溯:根据结果推结论 """ # 如何编写代码完成 # 目标人物的年龄 = 后一排年龄 + 2 # 后一排年龄 = 后后一排年龄 + 2 # 后后一排年龄 = 后后后一排年龄 + 2 # 后后后后一排年龄 = 18 # 将求问年龄变成函数 # age(5) = age(4) + 2 # age(4) = age(3) + 2 # age(3) = age(2) + 2 # age(2) = age(1) + 2 # age(1) = 18 # 封装函数 def get_age(n): if n == 1: return 18 # 有明确的结束条件 return get_age(n-1) + 2 print(get_age(4))
递归练习
l1 = [1,[2,[3,[4,[5,[6,[7,[8,[9,]]]]]]]]] '''需求:循环打印出列表中每一个数字''' # 写代码之前一定要先理清思路 """ 完整步骤 1.for循环大列表 2.判断元素是否是数字 如果是则打印 3.如果不是则for循环 4.判断元素是否是数字 如果是则打印 5.如果不是则for循环 6.判断元素是否是数字 如果是则打印 7.如果不是则for循环 ps:重复做一些事情 但是每次都比上一次简单一些 >>>: 递归函数 """ def get_num(l): for i in l: # 自带结束条件 并且每次传入的数据都比上一次简单 if isinstance(i,int): # 判断某个数据是否属于某个类型 print(i) else: get_num(i) get_num(l1)
算法
算法的概念
# 算法其实就是解决问题的有效方法 """ 算法比较偏向于学术研究 很枯燥 并且产出很少 甚至只有非常大的互联网公司才会有算法部分 算法工程师薪资待遇很高 但是产出很少 有时候甚至几年都没有任何的成果 有点类似于研究所!!! """
算法之二分法
会二分法是算法里最基本的要求
二分法原理及缺陷
# 二分法的前提即限制条件 1.二分法使用有前提: 数据集必须有先后顺序(升序 降序) 2.不能出现除数字类型外的其他数据类型 """ 二分法原理 获取数据集中间的元素 比对大小 如果中间的元素大于目标数据 那么保留数据集的左边一半 如果中间的元素小于目标数据 那么保留数据集的右边一半 然后针对剩下的数据集再二分 如果中间的元素大于目标数据 那么保留数据集的左边一半 如果中间的元素小于目标数据 那么保留数据集的右边一半 ... """ # 二分法的缺陷 1.如果要找的元素就在数据集的开头 二分更加复杂 2.数据集必须有顺序 '目前没有最完美的算法 都有相应的限制条件'
实际应用
l1 = [13,21,35,46,52,67,76,87,99,123,213,321,432,564,612] # 查找一个数 123 def get_target(l1,target_num): # 最后需要考虑找不到的情况 l1不可能无限制二分 if len(l1) == 0: print('不好意思 真的没有 找不到') return # 1.获取中间元素的索引值(只能是整数) middle_index = len(l1) // 2 # 2.判断中间索引对应的数据与目标数据的大小 if target_num > l1[middle_index]: # 3.保留数据集右侧 l1_left = l1[middle_index+1:] # 3.1.对右侧继续二分 重复执行相同代码 并且复杂度降低 print(l1_left) get_target(l1_left,target_num) elif target_num < l1[middle_index]: # 4.保留数据集左侧 l1_right = l1[:middle_index] print(l1_right) # 4.1.对右侧继续二分 重复执行相同代码 并且复杂度降低 get_target(l1_right,target_num) else: print('找到了',target_num) get_target(l1,99)
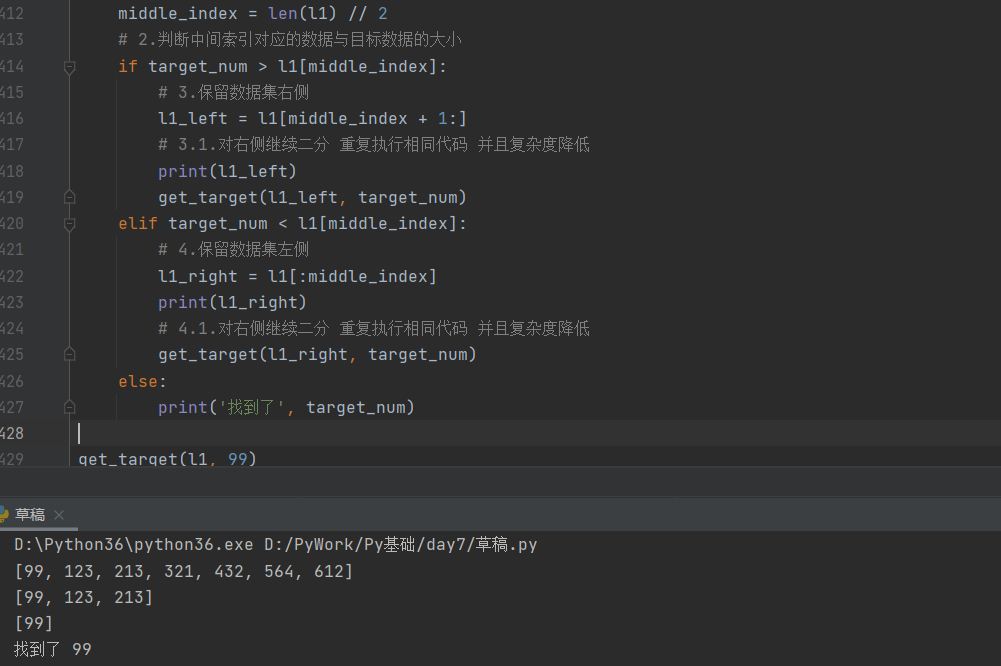
---------------------------------------------------------------------------------------------------------------------

本文来自博客园,作者:{Mr_胡萝卜须},转载请注明原文链接:https://www.cnblogs.com/Mr-fang/p/16035039.html




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· winform 绘制太阳,地球,月球 运作规律
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人