树
树
树形结构是一类重要的非线性结构。树形结构是节点之间有分支，并具有层次关系的结构。
特殊且重要：树中的节点，只有一个直接的前驱，有n个直接的后继。
比如：家谱
一、树的定义
树(tree)是包含n(n>0)个结点的有穷集。树中每个元素用结点来表示。
树的递归定义刻画了树的固有特性：一棵非空树是由若干棵子树构成的，而子树又可由若干棵更小的子 树构成。
树也可以理解：是由根结点和若干棵子树构成。
二、树形结构基本术语
1、节点的度：一个节点含有的子树的个数称为该节点的度。
2、树的度：一棵树中，最大的节点的度称为树的度。
3、叶节点（终端节点）：度为0的节点。
4、分支节点（非终端节点）：度不为0的节点。
5、孩子和双亲：树中某个节点的子树之根称为该节点的孩子或儿子，相应地，该节点称为孩子的双亲或 父亲。同一个双亲的孩子称为兄弟。
6、祖先和子孙：以某节点为根的子树中任一节点都称为该节点的子孙。相反，这个子孙节点沿父节点往 上直至根节点的任一节点称为祖先。
7、节点的层：从根开始定义起，根为第1层，根的子节点为第2层，以此类推。 8、树的高度或深度：树中节点的最大层次。
9、森林：由m(m>=0)棵互不相交的树的集合称为森林。
10、有序树和无序树：树中任意节点的子结点之间有顺序关系，这种树称为有序树。反之树中任意节点 的子结点之间没有顺序关系，这种树称为无序树,也称为自由树
三、树形结构的逻辑特征
1、树中任意一节点都可以有零个或多个直接后继（即孩子）节点，但至多只能有一个直接前趋（即双 亲）节点。
2、树中只有根节点无前趋，它是开始节点；叶节点无后继，它们是终端节点。
3、祖先与子孙的关系是对父子关系的延拓，它定义了树中节点之间的纵向次序。
4、有序树中，同一组兄弟节点从左到右有长幼之分。
四、树形结构的代码示例
模板类
template<class T>
class CMyTree_List
{
struct TreeNode //私有结构，在类外不需要访问
{
T data; //数据域
TreeNode* parent; //父节点指针
TreeNode* brother; //兄弟节点指针
TreeNode* child; //子节点指针
};
TreeNode* pRoot; //根节点指针
public:
CMyTree_List();
~CMyTree_List();
void clear(); //仅仅是一个接口,清除
bool find(T const& findData) const; //仅仅是一个接口,查找
void insert(T const& insertData, T const& findData,bool isChild = true); //插入节点：参数1：要插入节点；参数2：插入位置；参数3：默认为插入孩子
private:
void _clear(TreeNode* root); //真正用来做删除的递归函数
TreeNode* _find(TreeNode* root, T const& findData) const
{
if (root)
{
if (root->data == findData)
return root;
TreeNode* tempNode = _find(root->brother,findData);
if (tempNode)
return tempNode;
return _find(root->child, findData);
}
return nullptr;
}
};
template<class T>
void CMyTree_List<T>::insert(T const& insertData, T const& findData, bool isChild)
{
TreeNode* temp = new TreeNode;
temp->data = insertData;
temp->parent = nullptr;
temp->brother = nullptr;
temp->child = nullptr;
//准备好了一个可以插入到树中的新结点
if (pRoot)
{
TreeNode* findNode = _find(pRoot, findData);
if (findNode)
{
//表示找到了插入结点的位置
if (isChild)
{
//在该位置的子节点处插入
if (findNode->child)
{//存在子节点
TreeNode* tempNode = findNode->child;
while (tempNode->brother)//看子节点的兄弟节点存不存在
{
tempNode = tempNode->brother;//找到最后一个兄弟节点
}
tempNode->brother = temp;//插入新节点
temp->parent = tempNode->parent;
}
else
{//该位置子节点不存在
findNode->child = temp;
temp->parent = findNode;
}
}
else
{
//在该位置的兄弟结点处插入(有序)
while (findNode->brother)
{
findNode = findNode->brother;//找最后一个兄弟
}
findNode->brother = temp;//插入新结点成为新的兄弟
temp->parent = findNode->parent;//兄弟的父亲成为新节点的父亲
}
}
else
{
//表示在树中没有找到插入的位置
//自定义规则
delete temp;
return;
}
}
else
{
pRoot = temp;//空树做插入
}
}
template<class T>
bool CMyTree_List<T>::find(T const& findData) const
{
return _find(pRoot, findData) != nullptr;
}
template<class T>
void CMyTree_List<T>::_clear(TreeNode* root)
{
if (root)
{
_clear(root->brother);
_clear(root->child);
delete root;
root = nullptr;
}
}
template<class T>
void CMyTree_List<T>::clear()
{
_clear(pRoot);
}
template<class T>
CMyTree_List<T>::~CMyTree_List()
{
clear();
}
template<class T>
CMyTree_List<T>::CMyTree_List()
{
pRoot = nullptr;
}
int main()
{
CMyTree_List<int> cm;
cm.insert(2, 1);
cm.insert(3, 1);
cm.insert(4, 1);
cm.insert(5, 2);
cm.insert(6, 5, false);
system("pause");
return 0;
}
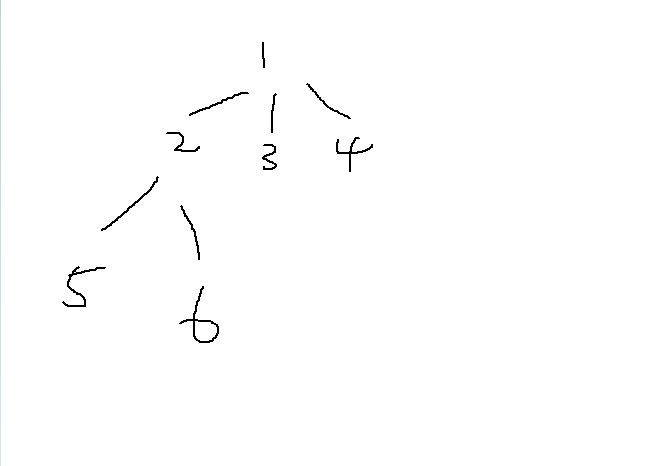
插入的树为：
