前缀中缀后缀表达式

前缀中缀后缀表达式

前缀表达式(波兰式)：例如：- × + 2 3 4 5

前缀表达式的计算求值：

从右至左扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算，并将结果入栈；重复上述过程直到表达式最左端，最后运算得出的值即为表达式的结果。
例如前缀表达式“- × + 2 3 4 5”：
(1) 从右至左扫描，将5、4、3、2压入堆栈；
(2) 遇到+运算符，因此弹出2和3（2为栈顶元素，3为次顶元素，注意与后缀表达式做比较），计算出2+3的值，得5，再将5入栈；
(3) 接下来是×运算符，因此弹出5和4，计算出5×4=20，将20入栈；
(4) 最后是-运算符，计算出20-5的值，即15，由此得出最终结果。
可以看出，用计算机计算前缀表达式的值是很容易的。

前缀表达式转中缀表达式

中缀表达式：例如: (2+ 3) × 4 - 5

中缀表达式转后缀表达式：

中缀直接转后缀方法：将中缀表达式每一步都加上括号，然后将运算符移动到对应括号的后面，最后去掉括号

如： (2+ 3) × 4 - 5 变为 (((2+3) × 4) - 5) 再将运算符移到后面，(((2 3) + 4)× 5) - 再去掉括号就变为后缀表达式2 3 + 4 × 5 -

中缀表达式转前缀表达式：

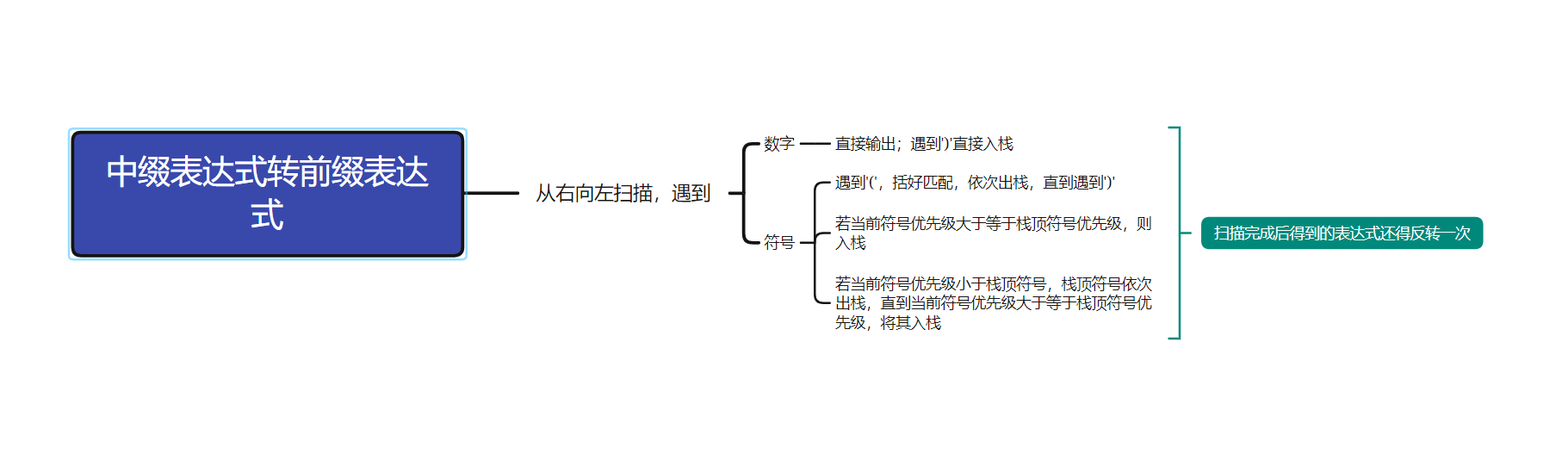
中缀直接转前缀方法：将中缀表达式每一步都加上括号，然后将运算符移动到对应括号的前面，最后去掉括号

如： (2+ 3) × 4 - 5 变为 (((2+3) × 4) - 5) 再将运算符移到后面，-(×(+(2 3) 4)× 5) - 再去掉括号就变为后缀表达式- × + 2 3 4 5

后缀表达式(逆波兰式)：例如：2 3 + 4 × 5 -

后缀表达式的计算求值：

与前缀表达式类似，只是顺序是从左至右：
从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算，并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果。
例如后缀表达式“2 3 + 4 × 5 -”：
(1) 从左至右扫描，将2和3压入堆栈；
(2) 遇到+运算符，因此弹出2和3（3为栈顶元素，2为次顶元素，注意与前缀表达式做比较），计算出2+3的值，得5，再将5入栈；
(3) 将4入栈；
(4) 接下来是×运算符，因此弹出5和4，计算出5×4=20，将20入栈；
(5) 将5入栈；
(6) 最后是-运算符，计算出20-5的值，即15，由此得出最终结果。

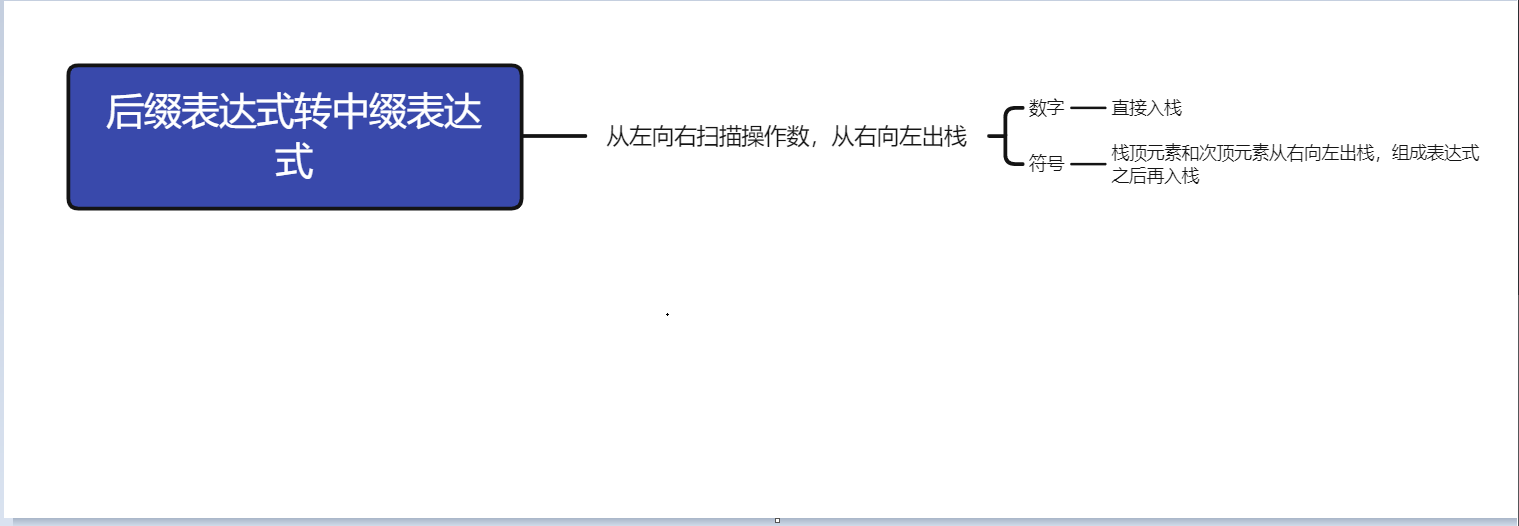
后缀表达式转中缀表达式：