线性规划中的单纯形法与内点法（原理、步骤以及matlab实现）（三）

在本系列的第三篇博客中，笔者讨论对偶单纯形法的相关理论和应用

2.3 Dual Simplex Method(对偶单纯形法)

Contents

　　2.3.1 对偶问题产生的原因

　　2.3.2 对偶问题的构造

　　2.3.3 对偶问题的相关定理

　　2.3.4 对偶问题的应用

 

2.3.1 对偶问题产生原因

在本系列的（二）中我们利用大M法和两阶段法解决一些不符合普通单纯形法标准形式的线性规划问题，不过大M法和两阶段法的使用步骤比较繁琐

下面考虑两个问题模型：

   

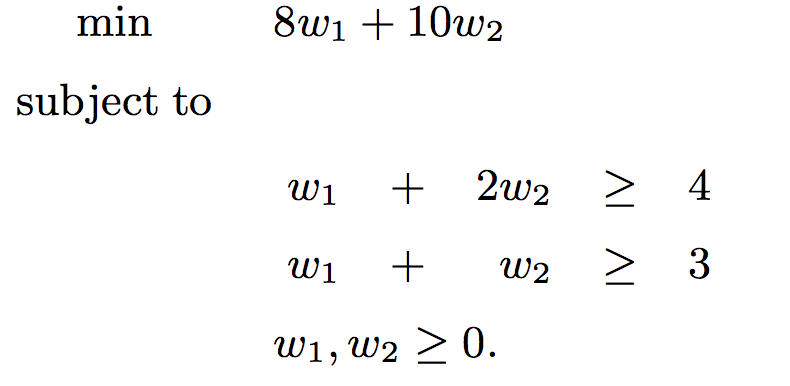
两个问题之间联系如下：

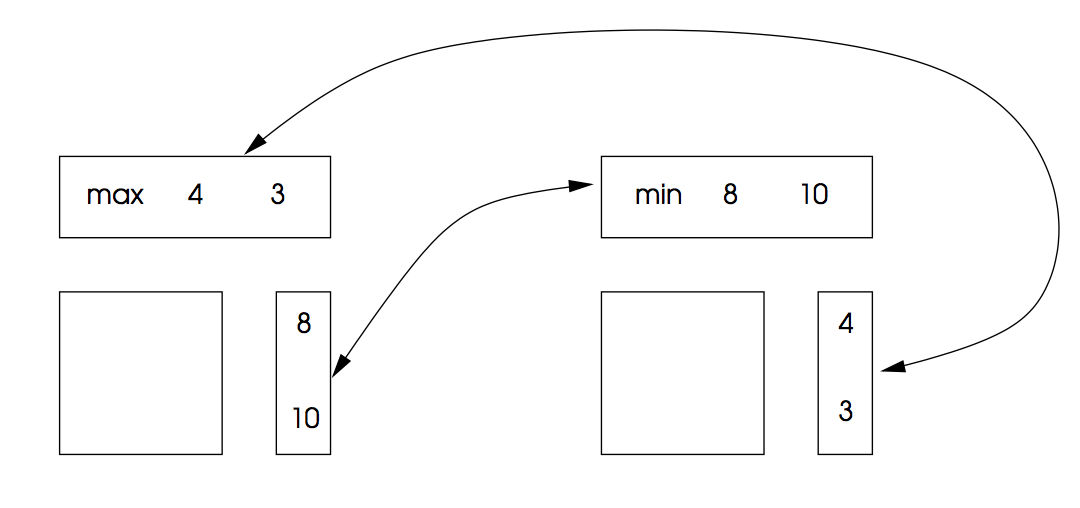
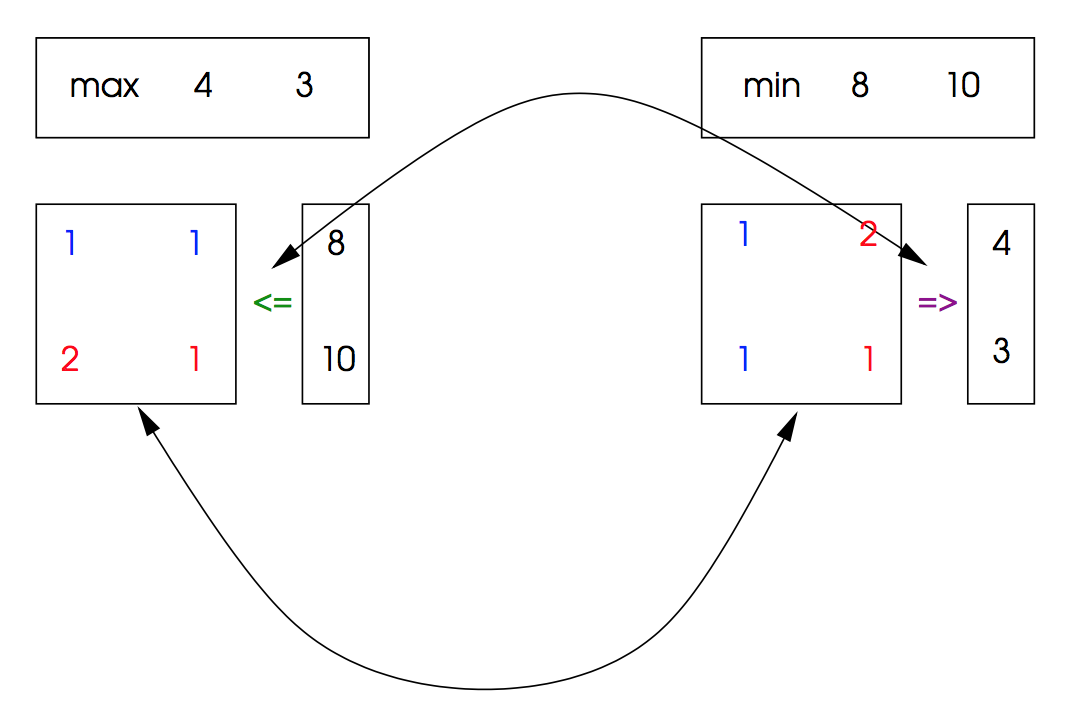
两个问题的解如下：

目标函数的目标值都是26

这里放出第一个问题最后的迭代结果：

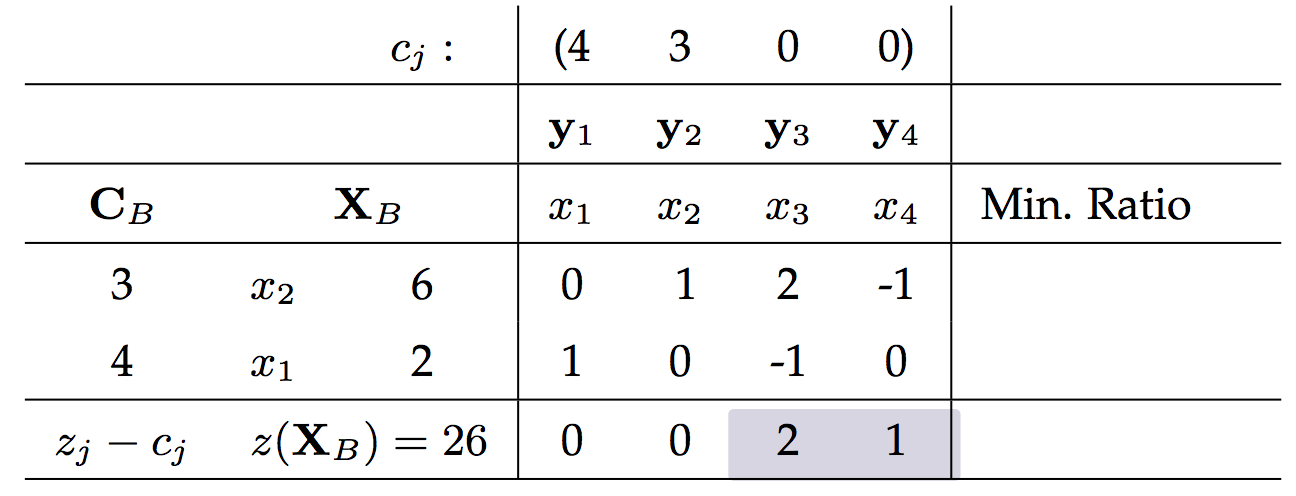
看到阴影部分的值正好是第二个问题的最优解，这里并不是巧合！！！

对偶性理论指出如果一个线性规划问题存在最优解，那么它的对偶问题也存在最优解，并且两者的结果一致！！

可以这样理解：类似于生产问题中的最大化收入的问题，等价于租用设备使得成本最小。

2.3.2 构造

 

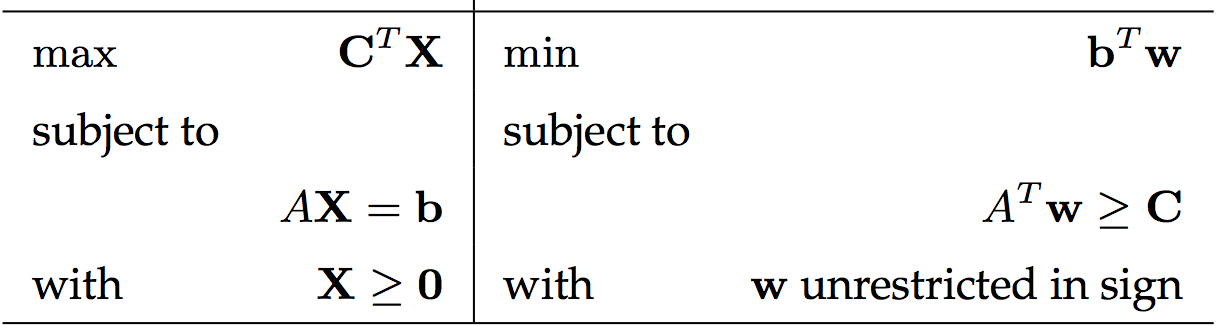
等式约束对应的对偶未知数没有非负限制

转化总结如下：

 

脑容量足够的朋友可以记一下这个：

不过，可以这样记住：

1.原问题转为最大化（最小化），约束符号全是≤（≥），注意这里的右端值没有非负限制！！！如此对偶未知数都是非负。

2.对于等式约束，对偶未知数没有非负限制

 

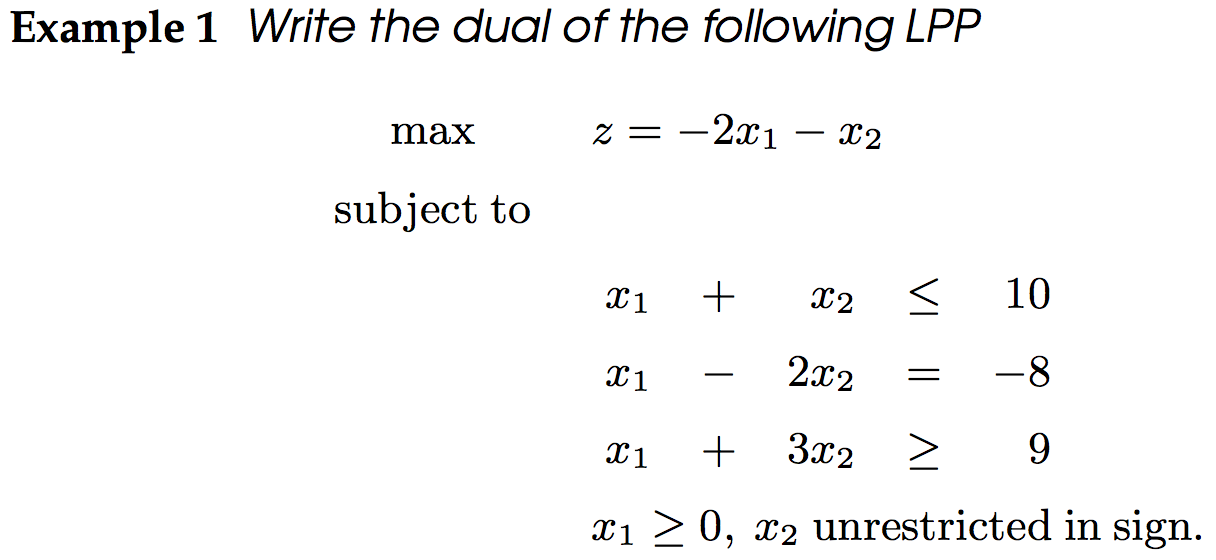
对偶格式为

 

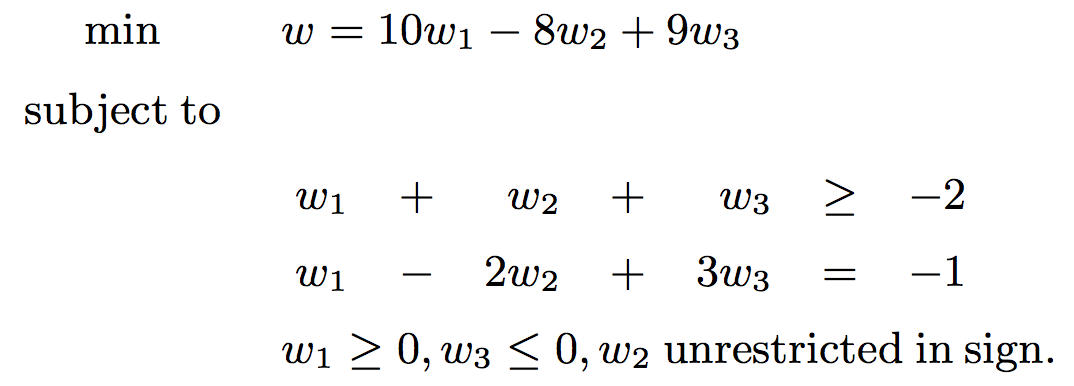
2.3.3 相关定理（原理）

弱对偶定理：

 

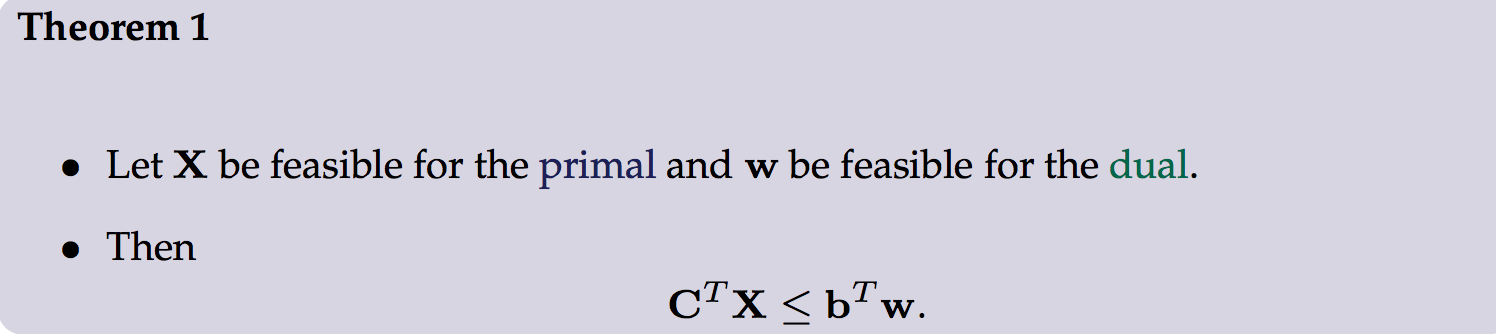
证明如下：

 

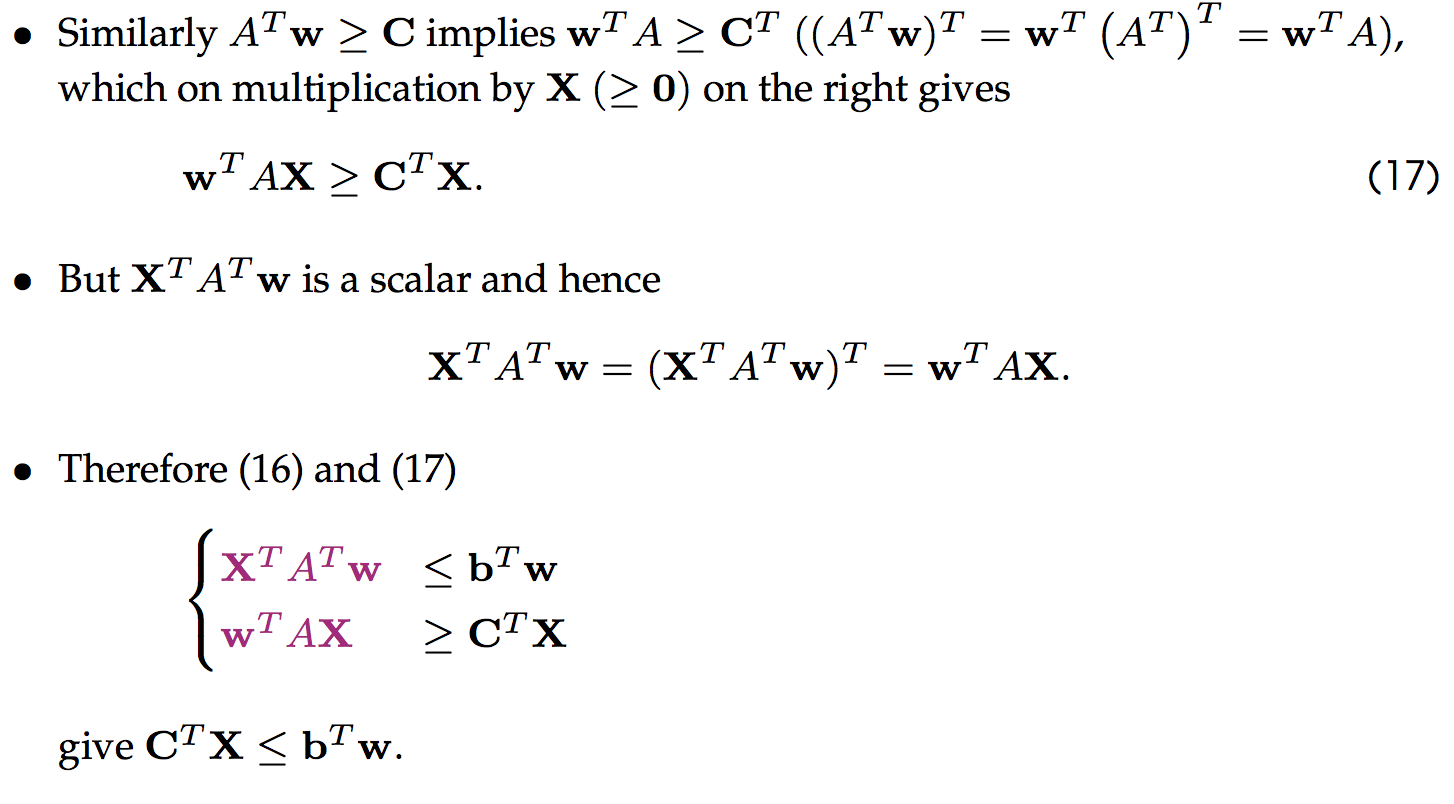
推论

证明：

 

强对偶定理：

 

以下是证明，核心思想是：在求出原问题最优解的时候，我们实际上也在求解对偶问题！！

 

得证

2.3.4 应用

 

先用matlab解出：

linprog():

 

f = [2 1];
A = [-4 -3; 1 2];
b = [-6 3];
Aeq = [3 1];
beq = [3];
lb = [0 0];
[x, fval] = linprog(f, A, b, Aeq, beq, lb)

 

 运行结果：

revised():

c = [-2 -1];
A = [3 1; 4 3; 1 2];
b = [3 6 3];
inq = [0 1 -1];
revised(c, b, A, inq, 0)

 运行结果：

现在转化为对偶问题来解答：

 

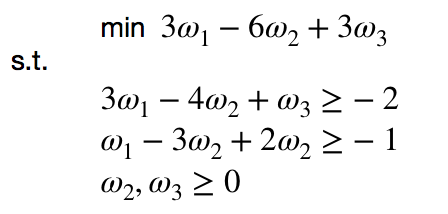
linprog()求解

f = [3 -6 3];
A = [-3 4 -1; -1 3 -2];
b = [2 1];
lb = [-inf, 0 0];
[x, fval] = linprog(f, A, b, [], [], lb)

 运行结果：

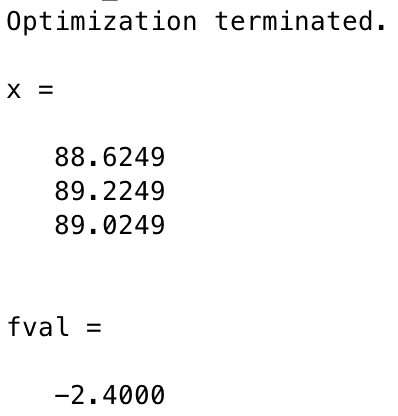
可以看到，目标方程的最优值是一样的