通俗易懂Apriori算法及Python实现
本篇分为三个部分:
一、算法背景
啤酒与尿布故事:
某超市为增加销售量,提取出了他们超市所有的销售记录进行分析。在对这些小票数据进行分析时,发现男性顾客在购买婴儿尿片时,通常会顺便搭配带打啤酒来犒劳自己,于是超市就想如果把这两种平时看不出有关联的商品摆在一起,是不是能方便顾客同时提升商品的销量。于是尝试将啤酒和尿布摆在一起的上柜策略,最后果然两样商品的销量双双提升。
聪明的现代店家(甩饼)故事:
甩饼是2020年的一个店家,他听了啤酒与尿布故事后在想能不能有种便捷的方法可以找出这些有关联商品。比如说,客人完成购买行为后,客人会有小票。店家会有相应的购买记录(客人一次购买行为,购买了什么物品)。那么甩饼就可以利用这些购买记录来进行分析!举个栗子
比如客人,小敏去甩饼超市买泡面,小敏饭量大,一桶面不够吃,两桶又吃不了,她就在想那就加个蛋吧?还不够!那再来根香肠!
其他很多客人都会有小敏这样的购物习惯
所以,泡面、卤蛋、香肠就极大可能成组合,出现在每张小票上。
通过看小票有哪些商品经常成组合出现,则它们极大可能是关联商品。
支持度:
甩饼要怎么通过这些小票记录找出这些关联商品呢?于是他学习了Apriori算法。Apriori算法认为,如果某一组商品组合在所有小票中出现的次数太少,那么我们就认这组的商品之间没有什么关联(例如:A是头孢、B是白酒,那么A和B基本上不可能同时出现在同一张小票上,那么可以推断出他们没有什么关联)
那么甩饼又在想,要这组商品组合要出现在少于多少张小票,我们就可以认为它里面的商品是无关联的呢?
这个次数可以任意规定,我们可以把小票的张数称为支持度。这个支持度不宜太大也不宜太小,如果这个支持度太大,那么很多商品本来有关联(比如方便面和火腿),结果因为支持度定太大,就只能认为他们无关联了(比如说有一百张小票,你非得要求一百张小票都要有方便面和火腿,才认为它们有关联)。那如果定的支持度太小,那么很多无关联的商品(比如头孢和酒)又太容易被看错成有关联(比如说有一百张小票,你只要求有一张小票同时出现头孢和酒,你就认为它们有关联)
所以这个值取值一定得合适,这个合适的支持度取值我们就称之为最小支持度(商品组合出现的小票张数多于这个值,这组商品就有关。如果低于这个值,这组商品就无关)
那么甩饼有了购买记录(客人购买的小票),选取好一个最小支持度。对于特定的商品组合,他只需看这组商品组合在小票同时出现的支持度(次数)是不是大于这个最小支持度就可以判断,这组商品是否有关联(有这组商品组合的小票张数是不是大于最小支持度)
举个栗子:
商店里有5种商品,今天开出了4张小票,每行对应一张小票(为了方便起见,把ABCDE换成数字 1 2 3 4 5):
[A C D] --> 1 3 4
[B C E] --> 2 3 5
[A B C E] --> 1 2 3 5
[B E] --> 2 5
这时A在三张小票中出现,那么A的支持度support(A)=3
AC商品组合在同样三张小票中出现,那么AC组合的支持度support(AC)=3
如果甩饼选择最小支持度min_support=2,那么即可认为商品组合支持度大于最小支持度的组内商品是有关联的
所以support(AC)>min_support 则A、C可认为有关联
二、算法介绍
先介绍两个定律:
Apriori定律1 :如果某商品组合小于最小支持度,则就将它舍去,它的超集必然不是频繁项集。
Apriori定律2 :如果一个集合是频繁项集,即这个商品组合支持度大于最小支持度,则它的所有子集都是频繁项集
为了方便对两个定律的理解,还是用之前的小票数据,分别举例说明:
[A C D] --> 1 3 4
[B C E] --> 2 3 5
[A B C E] --> 1 2 3 5
[B E] --> 2 5
1° 对于Apriori定律1,对于BC这个商品组合,它出现的次数为1,即support(BC)=1<min_support=2,那么对于他的超集如BCE,BCE出现的次数必不可能比BC出现的次数多,即support(BCE)<=support(BC)<min_support 所以BCE必不可能是频繁项集 (补充:当商品组合的支持度大于最小支持度,则认为该商品组合为频繁项集)
2° 对于Apriori定律2,基于Apriori定律1的很容易理解Apriori定律2。若AC的支持度大于2,那么A的支持度必大于2(AC都出现3次了,A当然也至少出现3次)
算法实现思路:
1、从一个商品开始找,找出所有的频繁项集(就是该商品的支持度大于最小支持度)
2、根据频繁项集确认下一组候选集
3、从候选集筛选频繁项集,从而递归步骤2、步骤3 ,直到不能递归为止
过程如图所示:
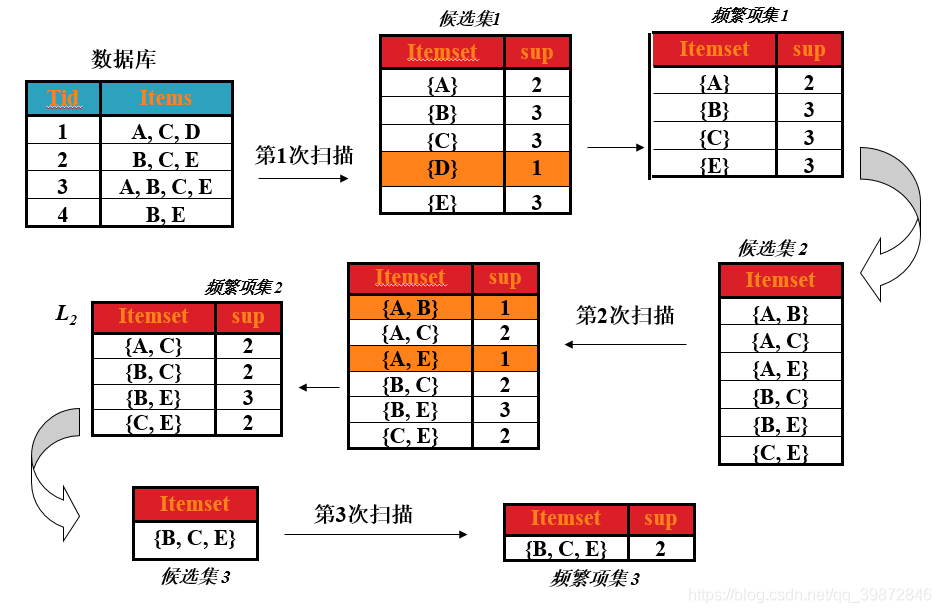
(1)第一次扫描
首先,求第一次扫描数据库后的候选集。
从图中可以看出,第一次扫描后,可以求出单个商品的支持度(图中支持度用出现次数表示),这个表称为第一次候选集,即下图所示:
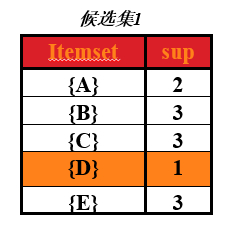
在第一次候选集基础上,求出第一次频繁项集,频繁项就是该商品的支持度 大于 最小支持度,支持度选择时随意的,在这里取最小支持度为 min_support=2
那么第一次频繁项集就是第一次候选集中,支持度大于或大于2的所有商品集合。即下表,(把 D 商品从表中去除了,因为它的支持度小于2)
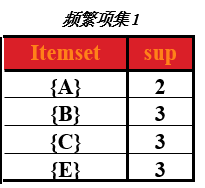
(2)第二次扫描
先求出第二次的候选集。
即在第一次频繁项集的基础上,找出第二次候选集,对商品进行组合,形成一个2元组,4种商品,不同组合有C42种,即 4x3=12 种,形成的表称为第二次候选集表。如下图

在求第二次频繁项集
对于上表,求出这两种商品同时出现在总记录中的次数(即求支持度),然后去掉支持度小于2的商品组合,形成的表即为第二次频繁项集。如下表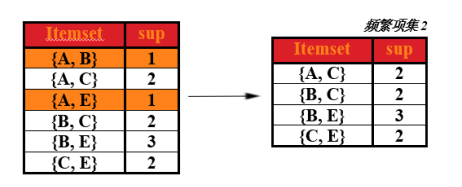
(3)第三次扫描
先求出第三次的候选集。
即在第二次频繁项集的基础上,找出第三次候选集。
就是将原来的2元组,拓展为3元组,怎么拓展呢?
设K为第K次扫描,要求第K个候选集,找出上一次扫描的频繁项集,然后观察里面的记录,对于里面的每个记录,前(K-2)个前缀相同的,归为一类,在同一类别中进行合并。
比如 这第三次扫描,要求出它的候选集,先找出上次扫描形成的第二次频繁项集表,里面有4条记录,分别为,AC,BC,BE,CE,这些记录中,前(K-2)个前缀,就是前(3-2)个前缀,也就是第一个前缀相同的归为一类,接着在属于同一类的记录中,进行合并,比如BC,BE,它门的第一个前缀都是B,那么在这一类中,把它门合并起来就形成了BCE。还剩下AC、CE,它门第一个前缀不相同,也没有其他元素和它门相同,那么就不用去管了。如果你非要合并,把AC、CE合并为ACE,我们看一下ACE的子集,它的子集是{AC、CE、AE},可以看出AC、CE确实是频繁项集,但是AE呢,你在求第二次的候选集时,因为AE的支持度小于2,你把它去除了,那么ACE也必然不是频繁项集。(Apriori定律1 :如果某商品组合小于最小支持度,则就将它舍去,它的超集必然不是频繁项集。)
减枝的概念:
比如刚才新形成的BCE这个组合,它的子集是{BC、CE、BE},显然BC和CE本来就是一个频繁项集,但是CE呢,我们必须对比上一次频繁项集中的元素,也就是第2次频繁项集的元素,如果CE不是第二次频繁项集的元素,那么就把新形成的 BC E 这个元素给 “减去”,也就是减枝,这一点我在代码中有体现,具体请看后面的代码。
(4)第四次扫描和前两次原理,一样,留给读者做练习。
最后值得一提的是,当最后生成的候选集表中,只有0个或1个的话,循环就结束了。
三、python代码实现
代码输出如下:
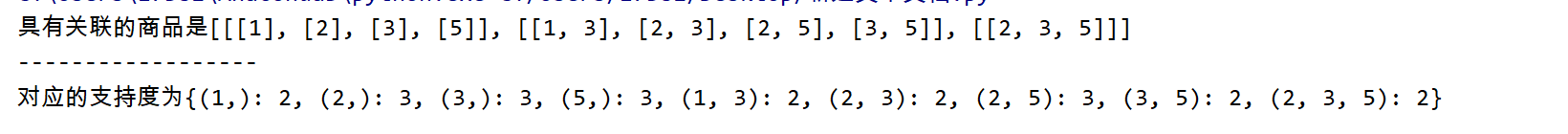
代码如下:
''' #请从最后的main方法开始看起 Apriori算法,频繁项集算法 A 1, B 2, C 3, D 4, E 5 1 [A C D] 1 3 4 2 [B C E] 2 3 5 3 [A B C E] 1 2 3 5 4 [B E] 2 5 min_support = 2 或 = 2/4 ''' def item(dataset): #求第一次扫描数据库后的 候选集,(它没法加入循环) c1 = [] #存放候选集元素 for x in dataset: #就是求这个数据库中出现了几个元素,然后返回 for y in x: if [y] not in c1: c1.append( [y] ) c1.sort() #print(c1) return c1 def get_frequent_item(dataset, c, min_support): cut_branch = {} #用来存放所有项集的支持度的字典 for x in c: for y in dataset: if set(x).issubset(set(y)): #如果 x 在 y中,就把对应元素后面加 1 cut_branch[tuple(x)] = cut_branch.get(tuple(x), 0) + 1 #cut_branch[y] = new_cand.get(y, 0)表示如果字典里面没有想要的关键词,就返回0 #print(cut_branch) Fk = [] #支持度大于最小支持度的项集, 即频繁项集 sup_dataK = {} #用来存放所有 频繁 项集的支持度的字典 for i in cut_branch: if cut_branch[i] >= min_support: #Apriori定律1 小于支持度,则就将它舍去,它的超集必然不是频繁项集 Fk.append( list(i)) sup_dataK[i] = cut_branch[i] #print(Fk) return Fk, sup_dataK def get_candidate(Fk, K): #求第k次候选集 ck = [] #存放产生候选集 for i in range(len(Fk)): for j in range(i+1, len(Fk)): L1 = list(Fk[i])[:K-2] L2 = list(Fk[j])[:K-2] L1.sort() L2.sort() #先排序,在进行组合 if L1 == L2: if K > 2: #第二次求候选集,不需要进行减枝,因为第一次候选集都是单元素,且已经减枝了,组合为双元素肯定不会出现不满足支持度的元素 new = list(set(Fk[i]) ^ set(Fk[j]) ) #集合运算 对称差集 ^ (含义,集合的元素在t或s中,但不会同时出现在二者中) #new表示,这两个记录中,不同的元素集合 # 为什么要用new? 比如 1,2 1,3 两个合并成 1,2,3 我们知道1,2 和 1,3 一定是频繁项集,但 2,3呢,我们要判断2,3是否为频繁项集 #Apriori定律1 如果一个集合不是频繁项集,则它的所有超集都不是频繁项集 else: new = set() for x in Fk: if set(new).issubset(set(x)) and list(set(Fk[i]) | set(Fk[j])) not in ck: #减枝 new是 x 的子集,并且 还没有加入 ck 中 ck.append( list(set(Fk[i]) | set(Fk[j])) ) #print(ck) return ck def Apriori(dataset, min_support = 2): c1 = item (dataset) #返回一个二维列表,里面的每一个一维列表,都是第一次候选集的元素 f1, sup_1 = get_frequent_item(dataset, c1, min_support) #求第一次候选集 F = [f1] #将第一次候选集产生的频繁项集放入 F ,以后每次扫描产生的所有频繁项集都放入里面 sup_data = sup_1 #一个字典,里面存放所有产生的候选集,及其支持度 K = 2 #从第二个开始循环求解,先求候选集,在求频繁项集 while (len(F[K-2]) > 1): #k-2是因为F是从0开始数的 #前一个的频繁项集个数在2个或2个以上,才继续循环,否则退出 ck = get_candidate(F[K-2], K) #求第k次候选集 fk, sup_k = get_frequent_item(dataset, ck, min_support) #求第k次频繁项集 F.append(fk) #把新产生的候选集假如F sup_data.update(sup_k) #字典更新,加入新得出的数据 K+=1 return F, sup_data #返回所有频繁项集, 以及存放频繁项集支持度的字典 if __name__ == '__main__': dataset = [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]] #装入数据 二维列表 F, sup_data = Apriori(dataset, min_support = 2) #最小支持度设置为2 print("具有关联的商品是{}".format(F)) #带变量的字符串输出,必须为字典符号表示 print('------------------') print("对应的支持度为{}".format(sup_data))
博文内容改自:https://blog.csdn.net/qq_39872846/article/details/105291265

