P9915 「RiOI-03」3-2

Question 问题 P9915 「RiOI-03」3-2

给定一个正整数 \(n\)。将 \([0,2^n)\) 中每个整数的二进制最低 \(n\) 位从低到高依次写在一个 \(2^n\times n\) 的矩阵上。矩阵两维的下标都从 \(0\) 开始。 如，当 \(n=3\) 时，矩阵是这样的：

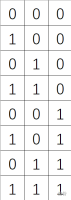
给定 \(q\) 次询问，每次询问这个矩阵下标为 \((x,y)\) 的格子所在的四连通块大小对 \(998244353\) 取模的值。

Solution 数学（观察性质）

应该是本题最简单，容易理解和实现的方法。

首先判断这个位置 \((x,y)\) 是否为 \(1~\text{or}~0\) 是简单的，(x>>y)&1 即可。

打表观察方案，发现连通块大小必然是 \(2^m-1\)，简要证明：观察到每个连通块都可以拆成 \(\sum_{i=0}^{m} 2^i\)，该式子的值为：\(2^{m+1}\)。

同时由上面的简要证明可知，从当前位置开始往右走，假设到 \((x,r)\) 时与原位置的数不一致或者向右走出表格外（此时 \(r=n\)），那么当前位置所处的连通块的大小即为 \(2^r-1\)。

一个优化：在 \(y \ge 60\) 时，直接输出 \(2^n-1\) 即可，因为此时该位置必然处于最大连通块。同时也避免了 \(2^y\) 超出 long long 范围的错误（准确来说，这是未定义行为）。

Code 代码

int n,q;
ll x,y;
inline ll two(int p){
	ll res=1,a=2;
	while(p){
		if(p&1) res=res*a%mod;
		a=a*a%mod;
		p>>=1;
	}
	return res%mod;
}//2^n 快速幂
inline bool check(ll x,ll y){return ((x>>y)&1);}//改位置为1或0
signed main(){
	read(n,q);ll num=two(n);
	for(rint i=1;i<=q;i++){
		read(x,y);
		if(y>=60){//特判
			printf("%lld\n",num-1);
			continue;
		}
		int t=check(x,y);//当前位置的数
		while(check(x,y)==t&&y<n) y++;//若不同则停止，相同则往右走
		printf("%lld\n",two(y)-1);//y不需要-1，请自行思考原因
	}
    return 0;
}