11.8 模拟赛小记
菜哭了。不会打，看了半个小时史铁生散文集。
100+0+80+0 喵。
正解是最小生成树。我的思路差不多。
为了全部联通，需要 n-1 条边。随意先计算给定的确定起始点的边，根据边权排序，从中挑至少 \(n-1-k\) 条边。剩下的用第二种边，每加一条边就能将两个联通块合并。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e6+10;
ll ans;
int n,m,k,w,cnt;
int fa[N];
struct node{int u,v,z;}r[N];
bool cmp(node a,node b){return a.z<b.z;}
int fd(int x){
if(fa[x]==x) return x;
return fa[x]=fd(fa[x]);
}
void mer(int x,int y,int z){
x=fd(x),y=fd(y);
if(x==y) return;
fa[x]=y;
ans+=z;
cnt++;
}
int main(){
freopen("constructure.in","r",stdin);
freopen("constructure.out","w",stdout);
scanf("%d%d%d%d",&n,&m,&k,&w);
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=m;i++)
scanf("%d%d%d",&r[i].u,&r[i].v,&r[i].z);
sort(r+1,r+m+1,cmp);
for(int i=1;i<=m;i++){
if(r[i].z>w&&cnt>=n-1-k) break;
mer(r[i].u,r[i].v,r[i].z);
}
for(int i=1;i<=n;i++)
if(fd(i)==i) ans+=w;
ans-=w;
printf("%lld",ans);
}
求最大面积的矩阵，该矩阵的所有子矩阵均满足对任意 \(i,j\) 都有 \(A_{1,1}+A_{i,j}<=A_{1,j}+A_{i,1}\)
赛时暴力写了 N 的好多好多好多次方然后把自己气笑了，再没看这个题。
正解，考虑先从小的角度入手，显然 \(1*n\) 的矩阵和 \(n*1\) 的矩阵都是满足要求的；再去想 \(2*n\) 的矩阵：
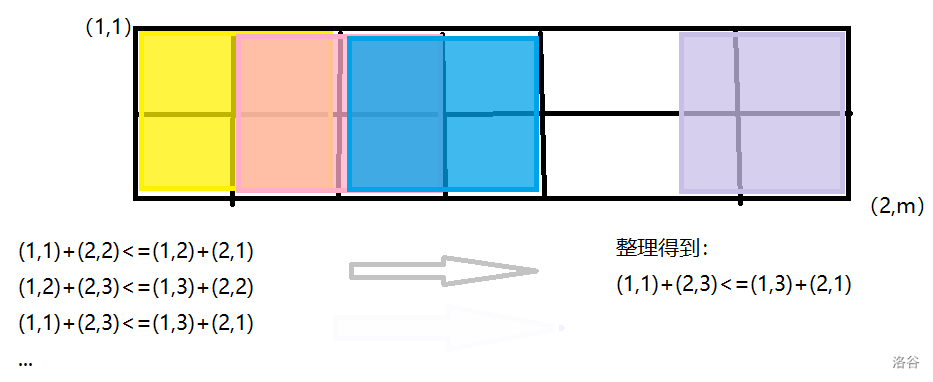
整理发现，为了确定这个矩阵是否满足条件，实质上是在求这个矩阵中除了最后一行、最后一列，以其他所有点为左上角的 \(2*2\) 的子矩阵是否满足。
这其实是通过归纳法来证明结论。由小见大。
然后问题转换为了：对于每个点为 \(2*2\) 子矩阵的左上角来预处理这个点是否合法。最后求面积最大的矩阵，实际上就是求最大全 1 矩阵面积。
这就是一个很典的单调栈问题了。在这篇博客里我有再整理单调栈。
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,m;
int a[N][N],b[N][N];
int g[N],s[N],w[N],top,ans;
struct node{int g,wz;}S[N];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) scanf("%d",&b[i][j]);
for(int i=1;i<n;i++){
for(int j=1;j<m;j++){
if(b[i][j]+b[i+1][j+1]<=b[i][j+1]+b[i+1][j]) a[i][j]=1;
else a[i][j]=0;
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if((a[i][j]==a[i-1][j]||i==1)&&a[i][j]) g[j]++;
else if(a[i][j]) g[j]=1;
else g[j]=0;
}
top=0;
g[m+1]=0;
for(int j=1;j<=m+1;j++){
int kuan=0;
while(g[j]<s[top]){
kuan+=w[top];
ans=max(ans,(kuan+1)*(s[top]+1));
top--;
}
s[++top]=g[j];
w[top]=kuan+1;
}
}
ans=max(ans,max(n,m));
printf("%d",ans);
}
给一个由 \([1,n]\) 构成的排列，求一个逆序对数与之相同，且字典序比之大的字典序最小的序列。
没想到吧，next_permutation 暴力枚举序列竟然有 80pts。
找到一个位置 i，使前 i-1 与原序列相同。可以二分出 i，使答案序列 1~i-1位与原序列相同，后面的也是确定的所以也可以二分。
因为我不太懂啊。所以鸽了，没补。
好像，多少和博弈论沾些边了。所以我不补。
