笛卡尔树 学习笔记

笛卡尔树 学习笔记

定义

笛卡尔树是一棵特殊的 BST，或者说特殊的堆，它既满足 BST 的性质又满足堆的性质。

一棵笛卡尔树的一个节点同时拥有两个权值，一个是 \(id\)，一个是 \(key\)，分别是 BST 和 堆 的权值，单看 \(id\) 值它是一棵 BST，单看 \(key\) 值他是一个堆。

例如 \(key\) 为 \(4,1,3,2,5\)，\(id\) 为 \(1,2,3,4,5\) 的笛卡尔树就是下图这样：

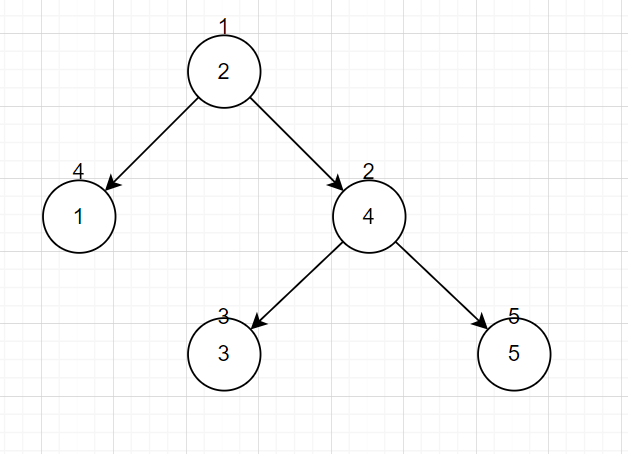
值得注意的是，如果 \(id\) 有序，每一种 \(key\) 和 \(id\) 序列所对应的笛卡尔树是唯一的，同时 \(\text{Treap}\) 也是一种笛卡尔树。

建树

既然 \(\text{Treap}\) 是笛卡尔树，按 \(\text{Treap}\) 的方法建树就好了，每次加入一个节点通过旋转维护堆的性质。

但是这样时间复杂度会是最坏 \(O(n^2)\) 的，一条链就可以卡掉，在 \(\text{Treap}\) 中保证复杂度的关键在随机权值，这样树的形态不固定，所以基本不会被卡掉。

实际上，如果 \(id\) 保证有序，有一种线性的方法可以建出一棵唯一的笛卡尔树。

考虑 \(id\) 递增的情况，这时候，每次新加入一个节点，为了维护 BST 的性质，它和上一个节点的位置关系只有两种可能：

1. 上一个节点是当前节点的左儿子
2. 当前节点是上一个节点的右儿子

界定是哪种情况就要依靠 \(key\) 值，将 \(key\) 值较小的作为父亲。

不过如果我们肤浅的把当前节点设为父亲是不行的，因为还需要考虑当前节点与父亲的关系，所以可以用一个单调栈维护所有未确定的点，新加入的时候就不断弹出栈顶直到栈顶元素 \(key\) 值小于当前元素 \(key\)，最后连边即可。

需要特殊判断当前节点没有弹出任何元素的情况，这种情况是没有左儿子的。

所以本质上单调栈维护了一条 BST 的最右链。

bool flg;
for(int i = 1; i <= n; i ++) {
    flg = 0;
    while(top && p[stk[top]] > p[i]) top --, flg = 1;
    rs[stk[top]] = i;
    if(flg) ls[i] = stk[top + 1];
    stk[++ top] = i;
}

加速 BST 建树

BST 很容易退化，如果暴力建树的话会爆炸。

可以给 BST 的 \(key\) 序列里面加一层 \(id\) 值，\(id\) 就是下标。这样保证了下标靠后的节点一定不会是下标靠前的节点的祖先，所以树的形态唯一确定，可以排序后，使用笛卡尔树的线性建树法。

如果 \(key\) 的值域较小可以使用桶排序，这样就是完全线性的了。

以下是：P1377 [TJOI2011] 树的序 的通过代码。

// Problem: P1377 [TJOI2011] 树的序
// Contest: Luogu
// Author: Moyou
// Copyright (c) 2023 Moyou All rights reserved.
// Date: 2023-09-02 01:37:58

#include <iostream>
using namespace std;
#define N 100005

int n, stk[N], top, ls[N], rs[N], b[N];
void print(int u) { // 题目要求先序遍历
    write(u), putchar(' ');
    if(ls[u]) print(ls[u]);
    if(rs[u]) print(rs[u]);
}

signed main() {
    n = read();
    for(int i = 1, x; i <= n; i ++) x = read(), b[x] = i;
    bool flg;
    for(int i = 1; i <= n; i ++) {
        flg = 0;
        while(top && b[stk[top]] > b[i]) top --, flg = 1;
        rs[stk[top]] = i; if(flg) ls[i] = stk[top + 1];
        stk[++ top] = i;
    }
    print(stk[1]);
    return 0;
}