[P3863] 序列 题解

[P3863] 序列 题解

题目描述

给定一个长度为 \(n\) 的序列，给出 \(q\) 个操作，形如：

\(1~l~r~x\) 表示将序列下标介于 \([l,r]\) 的元素加上 \(x\) （请注意，\(x\) 可能为负）

\(2~p~y\) 表示查询 \(a_p\) 在过去的多少秒时间内不小于 \(y\) （不包括这一秒，细节请参照样例）

开始时为第 \(0\) 秒，第 \(i\) 个操作发生在第 \(i\) 秒。

对于 \(100\%\) 的数据，保证 \(2 \leq n,q \leq 100000\)， \(1 \leq l \leq r \leq n\)， \(1 \leq p \leq n\)，\(-10^9 \leq x,y,a_i \leq 10^9\)

思路

先思考一个弱化版：\(n = 1\) 时，进行修改和询问。

那么这个问题就变为了一个下标为时间的序列，序列元素值为当前时间（下标）时，\(a_1\) 的值。

这个是分块的经典应用，当 \(n, q\) 同阶，可以在 \(O(n\sqrt n\log(\sqrt n))\) 解决此问题，参考 数列分块入门 2。

现在把问题拓展，\(n > 1\)。

如果以时间为 \(x\) 轴，序列元素为 \(y\) 轴，建立平面直角坐标系，用数据结构维护序列，那么，每个操作影响的区间如下图所示：

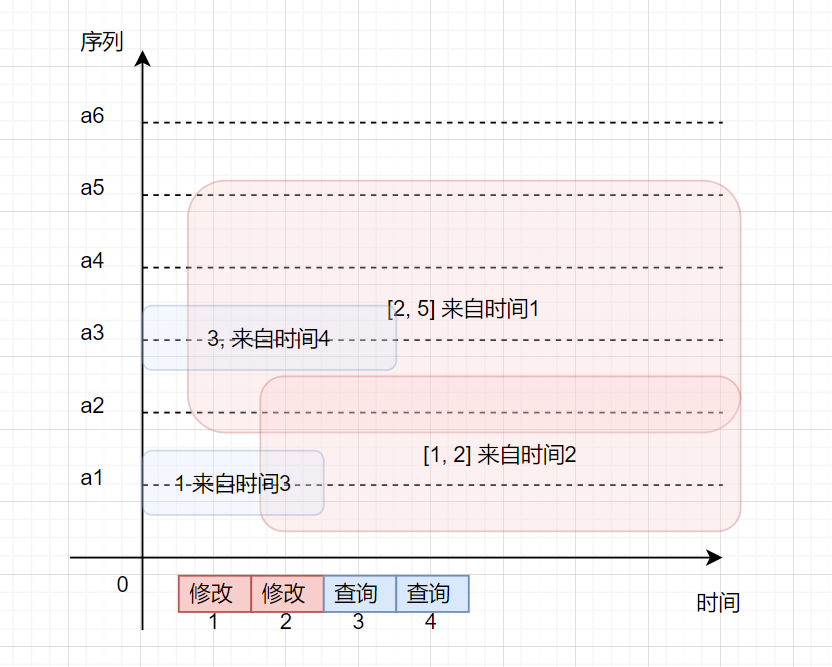
如图，如果我们按时间顺序去处理询问，会发现询问影响到的部分包括了之前的时间，这是很棘手的。

不过我们把屏幕旋转90°：

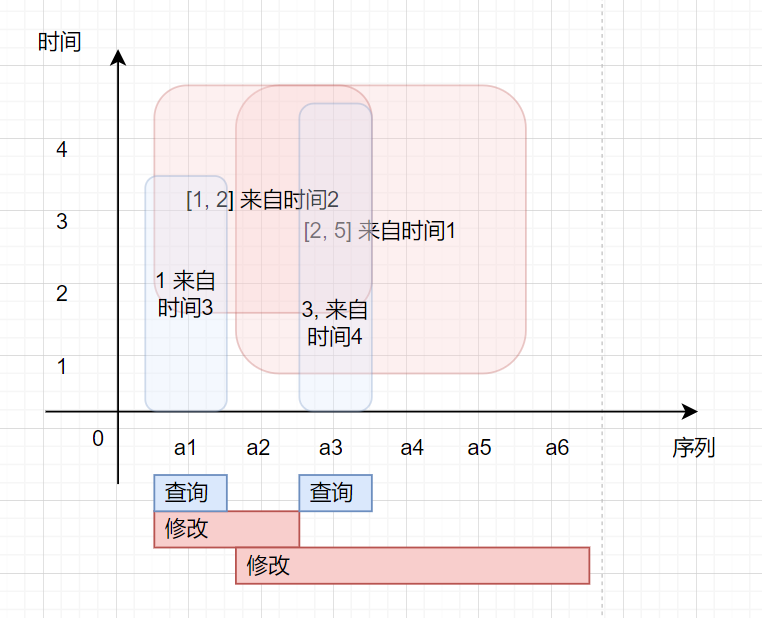
就会发现，如果以序列元素为 \(y\) 轴，时间为 \(x\) 轴，用数据结构维护时间，那么查询就变成了在数据结构上的区间查询。

哎呀，糟糕，现在修改变成了跨越多个 \(x\) 的棘手问题了，这该怎么办！

实际上，这个可以利用差分的思想解决，即在遍历到第 \(l\) 个序列下标时加上修改的影响，在遍历到第 \(r + 1\) 序列下标时消去这次修改的贡献。

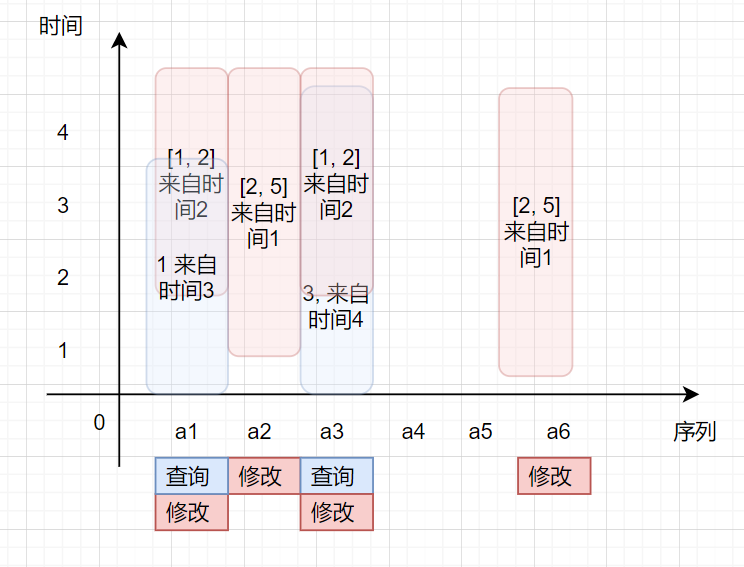
至于序列初始值，可以在查询的时候减去它，也可以作为操作挂在一开始。

当然，这个流程也可以理解为扫描线算法。

实现

离线，按序列下标排序，这个可以用 vector 把这些操作挂在序列下标上实现，然后用分块维护时间的序列。

总时间复杂度：\(O(n\sqrt n\log_2(\sqrt n) )\)

// Problem: P3863 序列
// Author: Moyou
// Copyright (c) 2023 Moyou All rights reserved.
// Date: 2023-05-20 08:47:18

#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
#include <queue>
#define speedup (ios::sync_with_stdio(0), cin.tie(0), cout.tie(0))
#define int long long
#define get(i) ((i - 1) / len + 1)

using namespace std;

const int N = 2e5 + 10, M = 450;

int a[N];
int bk[N], b[N], L[M], R[M], tag[M], len, tot; 
// 单点修改，区间查询多少个大于等于y
int n, T;

struct Options
{
    int op;
    int t, v;
} ;

vector<Options> q[N];

void reset(int k)
{
    for(int i = L[k]; i <= R[k]; i ++)
        b[i] = bk[i];
    sort(b + L[k], b + R[k] + 1);
}

void update(int p, int v)
{
    int l = p, r = T;
    if(get(l) == get(r))
    {
        for(int i = l; i <= r; i ++)
             bk[i] += v;
        reset(get(l));
    }
    else
    {
        for(int i = l; i <= R[get(l)]; i ++)
            bk[i] += v;
        reset(get(l));
        for(int i = L[get(r)]; i <= r; i ++)
            bk[i] += v;
        reset(get(r));
        for(int i = get(l) + 1; i <= get(r) - 1; i ++)
            tag[i] += v;
    }
    reset(get(p));
}

int query(int p, int x)
// 1 ~ p 中多少数>= x
{
    int l = 1, r = p, res = 0;
    if(get(l) == get(r))
    {
        for(int i = l; i <= r; i ++)
            if(bk[i] + tag[get(i)] >= x) res ++;
    }
    else
    {
        for(int i = l; i <= R[get(l)]; i ++)
            if(bk[i] + tag[get(i)] >= x) res ++;
        for(int i = L[get(r)]; i <= r; i ++)
            if(bk[i] + tag[get(i)] >= x) res ++;
        for(int i = get(l) + 1; i <= get(r) - 1; i ++)
        {
            int t = lower_bound(b + L[i], b + R[i] + 1, x - tag[i]) - b;
            if(b[t] >= x - tag[i]) res += R[i] - t + 1;
        }
    }
    return res;
}

int ans[N];

signed main()
{
    speedup;
    memset(ans, -1, sizeof ans);
    cin >> n >> T;
    for(int i = 1; i <= n; i ++)
        cin >> a[i];
    for(int i = 2, op, x, y, t; i <= T + 1; i ++) // 时间轴右移，给0时留出位置
    {
        cin >> op >> x >> y;
        if(op == 1)
        {
            cin >> t;
            q[x].push_back({op, i, t});
            q[y + 1].push_back({op, i, -t});
        }
        else
            q[x].push_back({op, i, y});
    }
         
    T ++;
    len = sqrt(T);
    tot = (T - 1) / len + 1;
    for(int i = 1; i <= tot; i ++)
        L[i] = (i - 1) * len + 1, R[i] = i * len;
    
    for(int i = 1; i <= n; i ++)
    {
        for(auto [op, tm, x] : q[i])
        {
            if(op == 1)
                update(tm, x);
            else
                ans[tm] = query(tm - 1, x - a[i]);
        }
    }
    
    for(int i = 1; i <= T; i ++)
        if(~ans[i]) cout << ans[i] << '\n';

    return 0;
}