[BZOJ2144] 跳跳棋 题解

[BZOJ2144] 跳跳棋 题解

题目传送门

建模

首先可以发现，对于每种状态最多只有三种变换方式。

分别对应：

1. 中间的棋子往左边跳
2. 中间的棋子往右边跳
3. 外面的棋子往中间跳，由于不能跳过两个棋子，因此只有唯一的变换方式

而在三个棋子相邻两个棋子的距离相等的时候，是没有办法进行变换 3 的。

如果把往中间跳得到的状态置为父亲，剩余两个状态置为儿子，这俨然就是一棵二叉树，根就是相邻两子距离相等的状态。

若令 \(dist[i, j]\) 表示从状态 \(i\) 变换到 \(j\) 所需的最少步数（这里 \(i\) 和 \(j\) 实际上体现为两个三元组）答案所求的两个状态 \(A, B\) 的最少变换次数，可以转化为：\(dist[A, B] = dist[A, LCA] + dist[LCA, B]\)。

因此只需要暴力让两个初始状态一起往上跳找到 \(LCA\) 就能得到答案。

优化

不过可以发现，这样搞太慢了，因此考虑优化。

对于 \(LCA\) 的求法，我们有很多高效的工具，但是这些算法在这题里面都不再适用，迫于数据范围的压力，我们连树的形态都无法得知，更别提预处理一堆东西了。

那么在这道题里面有什么特别之处吗，为了方便描述，以下称三个棋子所在的位置分别为 \(a, b, c\)，同时令 \(d_1 = b - a, d_2 = c - b\)，不失一般性地，我们假设 \(a < b < c, d_1 > d_2\)。

则进行一次变换 3 后得到的三个点为 \((a, 2b-c, b)\)，也可以表示为 \((a, b - d_2, c - d_2)\)。

考虑这么一种状态：\((0, 99998, 99999)\)，如果要一步步跳，我们会在路上浪费大量的时间。

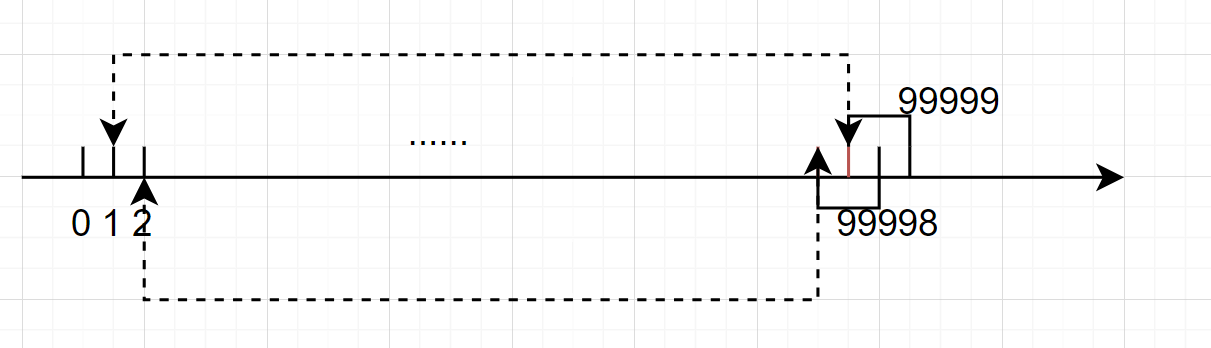
容易得到，路上一共会经过 \((d_1 - 1) / d_2\) 次变换，设其为 \(cnt\)。

则最后点的坐标为：\((a, b - cnt · d_2, c - cnt·d_2)\)。

\(d_1 < d_2\) 时同理。

重复进行以上步骤，直到 \(d_1 = d_2\)，这就找到了根，这类似于欧几里得算法（辗转相除），因此时间复杂度也是 \(O(\log n)\) 的。

然后类比 倍增法LCA，先让两个初始状态跳到同一层，然后一起往上跳。

只不过在这道题里，不能很方便地倍增地往上跳，容易发现，跳的步数满足二分性和单调性，因此可以用二分来替代这一操作。

具体而言就是二分一个步数，让两个状态一起往上跳这个步数，调整 \(l, r\) 即可。

代码实现

时间复杂度：\(O(\log n)\)

// Problem: P1852 跳跳棋
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1852
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Author: Moyou
// Copyright (c) 2023 Moyou All rights reserved.
// Date: 2023-02-25 20:04:48

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#define speedup (ios::sync_with_stdio(0), cin.tie(0), cout.tie(0))
using namespace std;

const int N = 1e5 + 10;

struct qwq
{
    int a, b, c, dep;
} p[5];

void up(int i, int k) // i 向上跳 k 步
{
    int d1 = p[i].b - p[i].a, d2 = p[i].c - p[i].b;
    while(d1 != d2 && k)
    {
        int cnt = 0;
        if(d1 > d2)
        {
            cnt = min((d1 - 1) / d2, k);
            k -= cnt, p[i].b -= cnt * d2, p[i].c -= cnt * d2;
        }
        else
        {
            cnt = min((d2 - 1) / d1, k);
            k -= cnt, p[i].a += cnt * d1, p[i].b += cnt * d1;
        }
        d1 = p[i].b - p[i].a, d2 = p[i].c - p[i].b;
    }
}

void print(int i) {printf("a: %d, b: %d, c: %d, dep: %d\n", p[i].a, p[i].b, p[i].c, p[i].dep); } // DEBUG 用

void toroot(int i) // 跳到根
{
    int d1 = p[i].b - p[i].a, d2 = p[i].c - p[i].b;
    while(d1 != d2)
    {
        int cnt = 0;
        if(d1 > d2)
        {
            cnt = (d1 - 1) / d2;
            p[i].dep += cnt, p[i].b -= cnt * d2, p[i].c -= cnt * d2;
        }
        else
        {
            cnt = (d2 - 1) / d1;
            p[i].dep += cnt, p[i].a += cnt * d1, p[i].b += cnt * d1;
        }
        d1 = p[i].b - p[i].a, d2 = p[i].c - p[i].b;
    }
}

int tmp[5];
int ans;

bool check(int k)
{
    auto t1 = p[3], t2 = p[4];
    up(3, k), up(4, k);
    bool flag = (p[3].a == p[4].a && p[3].b == p[4].b && p[3].c == p[4].c);
    p[3] = t1, p[4] = t2;
    return flag;
}

void LCA()
{
    if(p[3].dep > p[4].dep) swap(p[3], p[4]);
    ans = p[4].dep - p[3].dep;
    
    up(4, ans); // 4跳到3同一深度
    
    if(p[3].a == p[4].a && p[3].b == p[4].b && p[3].c == p[4].c)
    {
        printf("YES\n%d\n", ans);
        return; 
    }
    
    int l = 0, r = p[3].dep;
    int ttt = 0;
    while(l <= r)
    {
        int mid = l + r >> 1;
        if(check(mid)) ttt = mid, r = mid - 1;
        else l = mid + 1;
    }
    printf("YES\n%d\n", ans + ttt * 2);
}

int main()
{
    tmp[1] = read(), tmp[2] = read(), tmp[3] = read(), sort(tmp + 1, tmp + 4), p[1] = p[3] = {tmp[1], tmp[2], tmp[3], 0};
    tmp[1] = read(), tmp[2] = read(), tmp[3] = read(), sort(tmp + 1, tmp + 4), p[2] = p[4] = {tmp[1], tmp[2], tmp[3], 0};
    toroot(1), toroot(2);
    
    if(!(p[1].a == p[2].a && p[1].b == p[2].b && p[1].c == p[2].c)) // 不在同一个根上，必然无解
    {
        puts("NO");
        return 0;
    }
    
    p[3].dep = p[1].dep, p[4].dep = p[2].dep;
    // 否则找LCA，仿照树上倍增：
    
    LCA();

    return 0;
}