树链剖分学习笔记

树链剖分（Tree decomposition），顾名思义，是一种将树剖分为若干条链，使得可以用数据结构维护树上信息的数据结构。树链剖分有多种意思，包括重链剖分、长链剖分、实链剖分（LCT），本文介绍重链剖分。

定义

我们作出如下规定：

重子节点，表示一个节点的所有节点中子树最大的节点
轻子节点，表示一个节点中除重子节点以外的所有节点
重边，一个节点连向其重子节点的边被称为重边
轻边，一个节点连向其轻子节点的边被称为轻边
重链，一条由连续的重边组成的极大的链
不在任何一条重链内部的节点自成一条重链

如图

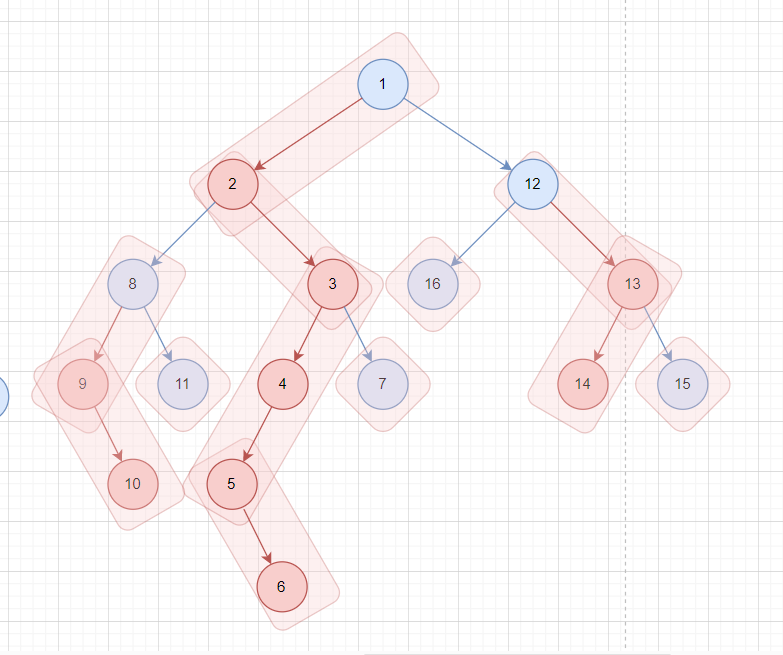
蓝色的节点表示轻节点，蓝色的边表示轻边，红色的反之，红色的框表示重链

性质

对于任意一条树上的路径 \(a\rightarrow b\)，都可以被拆分为 \(O(\log n)\) 条重链。

证明：由于任意一个 \(u\) 的子节点 \(v\) 如果子树大小 \(size_v> \dfrac12 size_u\)，那么 \(v\) 必定成为 \(u\) 的重儿子，反之，\(u\) 的轻儿子的子树大小最多为 \(\dfrac12 size_u\)。

因此从 \(\text{LCA}(a, b)\) 出发，每经过一条轻边，子树大小至少减少原来的 \(\dfrac12\)，换言之，最多经过 \(O(\log n)\) 条轻边，也就意味者有 \(O(\log n)\) 条重链。

如果 \(\text{Dfs}\) 时优先访问重节点（我形象地将其称为重度优先遍历），并进行重编号（\(\text{dfn}\)），同一条重链内的节点编号是连续的，又根据 \(\text{Dfs}\) 的性质，同一子树内的节点编号也是连续的。

利用性质二，我们可以方便地用数据结构（如线段树、树状数组等）维护重链内的信息，再根据性质一，我们最多需要进行 \(O(\log n)\) 此操作，若用线段树，可以做到 \(O(\log^2 n)\) 的每次操作时间复杂度，十分优秀。

实现

树链剖分在实现上有两个 \(\text{Dfs}\) 结构。

\(\text{Dfs1}\)

这遍 \(\text{Dfs}\) 用于处理树上基本信息。

解释一下变量的意思

\(id_i\) 表示 \(i\) 的重度优先遍历后的重编号
\(top_i\) 表示 \(i\) 所在的重链的顶端节点
\(hson_i\) 表示 \(i\) 的重子节点编号
\(timestamp\) 表示重度优先遍历的时间戳
\(fa_i\) 表示 \(i\) 的父亲编号
\(siz_i\) 表示 \(i\) 的子树大小
\(dep_i\) 表示 \(i\) 的深度

int id[N], top[N], hson[N], fa[N], siz[N], dep[N], timestamp;
void dfs1(int u, int f)
{
    fa[u] = f, dep[u] = dep[f] + 1, siz[u] = 1;
    int mx = -1;
    for (auto v : g[u])
    {
        if (v == f)
            continue;
        dfs1(v, u), siz[u] += siz[v];
        if (mx < siz[v]) hson[u] = v, mx = siz[v]; // 打擂台更新重儿子
    }
}

\(\text{Dfs2}\)

这遍 \(\text{Dfs}\) 即为重度优先遍历，记录重链上的信息

void dfs2(int u, int anc)
{
    id[u] = ++timestamp, top[u] = anc;
    if (!hson[u]) // 没有重儿子就返回
        return;
    dfs2(hson[u], anc); // 优先访问重儿子
    for (auto v : g[u])
    {
        if (v == hson[u] || v == fa[u]) // 遍历轻儿子
            continue;
        dfs2(v, v);
    }
}

查询 / 修改

查询的时候让两个点一起往上跳重链即可。

int Dquery(int u, int v) // 树剖 查询路径点权
{
    int ans = 0;
    while (top[u] != top[v]) // 一直跳到在同一条重链上
    {
        if (dep[top[u]] < dep[top[v]]) // 让深度小的先跳，不然会出事
            swap(u, v);
        ans = (ans + query(1, id[top[u]], id[u]).sum) % mod; // 查询重链内的信息，注意top[u] 的编号小于 u
        u = fa[top[u]];
    }
    if (dep[u] > dep[v])
        swap(u, v);
    return (ans + query(1, id[u], id[v]).sum) % mod; // 最后在同一重链内的信息直接查询
}

修改同理

void Dupdate(int u, int v, int delta) // 树剖 修改路径点权
{
    while (top[u] != top[v])
    {
        if (dep[top[u]] < dep[top[v]])
            swap(u, v);
        update(1, id[top[u]], id[u], delta);
        u = fa[top[u]];
    }
    if (dep[u] > dep[v])
        swap(u, v);
    update(1, id[u], id[v], delta);
}

应用

P3384 【模板】重链剖分/树链剖分

进行完树链剖分后在 \(id\) 序列上维护重链的信息即可。

对子树进行操作详见我的另一篇博客[POJ2763] Housewife Wind

// Problem: P3384 【模板】重链剖分/树链剖分
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3384
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Author: Moyou
// Copyright (c) 2023 Moyou All rights reserved.
// Date: 2023-02-05 15:47:22

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;

const int N = 1e5 + 10;

int n, m, root, mod;
int Temp[N], w[N];
vector<int> g[N];

struct owo // 多维护了一个量，无伤大雅owo
{
    int l, r, dat, sum, tag;
} tr[N << 2];

int id[N], top[N], hson[N], fa[N], siz[N], dep[N], timestamp;
void dfs1(int u, int f)
{
    fa[u] = f, dep[u] = dep[f] + 1, siz[u] = 1;
    int mx = -1;
    for (auto v : g[u])
    {
        if (v == f)
            continue;
        dfs1(v, u), siz[u] += siz[v];
        if (mx < siz[v])
            hson[u] = v, mx = siz[v];
    }
}

void dfs2(int u, int anc)
{
    id[u] = ++timestamp, top[u] = anc, w[id[u]] = Temp[u];
    if (!hson[u])
        return;
    dfs2(hson[u], anc);
    for (auto v : g[u])
    {
        if (v == hson[u] || v == fa[u])
            continue;
        dfs2(v, v);
    }
}

#define ls k << 1
#define rs k << 1 | 1
#define dat(k) tr[k].dat
#define sum(k) tr[k].sum
#define tag(k) tr[k].tag

inline owo up(owo k, owo l, owo r)
{
    k.dat = max(l.dat, r.dat), k.sum = (l.sum + r.sum) % mod;
    return k;
}

inline void up(int k)
{
    dat(k) = max(dat(ls), dat(rs)), sum(k) = (sum(ls) + sum(rs)) % mod;
}

inline void down(int k) // 懒标记下沉
{
    if (!tag(k))
        return;
    tag(ls) += tag(k), tag(rs) += tag(k), (sum(ls) += tag(k) * (tr[ls].r - tr[ls].l + 1)) %= mod,
        (sum(rs) += tag(k) * (tr[rs].r - tr[rs].l + 1)) %= mod, dat(ls) += tag(k), dat(rs) += tag(k), tag(k) = 0;
}

void build(int k, int l, int r) // 建线段树
{
    tr[k] = {l, r, 0, 0};
    if (l == r)
        tr[k] = {l, r, w[l], w[l], 0};
    else
    {
        int mid = l + r >> 1;
        build(ls, l, mid), build(rs, mid + 1, r), up(k);
    }
}

void update(int k, int ql, int qr, int v) // 线段树区间修改
{
    int l = tr[k].l, r = tr[k].r, mid = l + r >> 1;
    if (ql <= l && qr >= r)
    {
        sum(k) += v * (r - l + 1), tag(k) += v, dat(k) += v;
        return;
    }
    down(k);
    if (ql <= mid)
        update(ls, ql, qr, v);
    if (qr > mid)
        update(rs, ql, qr, v);
    up(k);
}

inline void update(int k, int v)
{
    update(1, id[k], id[k] + siz[k] - 1, v);
} // 修改子树内点权

owo query(int k, int ql, int qr) // 线段树区间查询
{
    int l = tr[k].l, r = tr[k].r, mid = l + r >> 1;
    if (ql <= l && qr >= r)
        return tr[k];
    down(k);
    owo tmp = {0, 0, 0, 0, 0}, L, R;
    if (ql > mid)
        return query(rs, ql, qr);
    if (qr <= mid)
        return query(ls, ql, qr);
    L = query(ls, ql, qr), R = query(rs, ql, qr);
    return up(tmp, L, R);
}

inline owo query(int k)
{
    return query(1, id[k], id[k] + siz[k] - 1);
} // 查询子树点权

int Dquery(int u, int v) // 树剖 查询路径点权
{
    int ans = 0;
    while (top[u] != top[v])
    {
        if (dep[top[u]] < dep[top[v]])
            swap(u, v);
        ans = (ans + query(1, id[top[u]], id[u]).sum) % mod;
        u = fa[top[u]];
    }
    if (dep[u] > dep[v])
        swap(u, v);
    return (ans + query(1, id[u], id[v]).sum) % mod;
}

void Dupdate(int u, int v, int delta) // 树剖 修改路径点权
{
    while (top[u] != top[v])
    {
        if (dep[top[u]] < dep[top[v]])
            swap(u, v);
        update(1, id[top[u]], id[u], delta);
        u = fa[top[u]];
    }
    if (dep[u] > dep[v])
        swap(u, v);
    update(1, id[u], id[v], delta);
}

#undef ls
#undef rs

int op, a, b, c;

int main()
{
    n = read(), m = read(), root = read(), mod = read();
    for (int i = 1; i <= n; i++)
        Temp[i] = read();
    for (int i = 1, a, b; i < n; i++)
    {
        a = read(), b = read();
        g[a].push_back(b), g[b].push_back(a);
    }
    dfs1(root, root);
    dfs2(root, root);
    build(1, 1, n);

    while (m--)
    {
        op = read();
        if (op == 4)
        {
            a = read();
            write(query(a).sum);
            putchar('\n');
        }
        if (op == 1)
        {
            a = read(), b = read(), c = read();
            c %= mod;
            Dupdate(a, b, c);
        }
        if (op == 2)
        {
            a = read(), b = read();
            write(Dquery(a, b));
            putchar('\n');
        }
        if (op == 3)
        {
            a = read(), b = read();
            update(a, b);
        }
    }
    return 0;
}

posted @ 2023-02-08 22:35 MoyouSayuki 阅读(29) 评论(0) 编辑收藏举报

刷新页面返回顶部

MoyouSayuki

树链剖分 学习笔记

树链剖分 学习笔记

定义

性质

实现

\(\text{Dfs1}\)

\(\text{Dfs2}\)

查询 / 修改

应用

公告

树链剖分学习笔记

树链剖分学习笔记