[UVA10559] Blocks 题解

[UVA10559] Blocks 题解

题目描述

有 \(n\) 个带有颜色的方块，每消除一段长度为 \(x\) 的连续的相同颜色的方块可以得到 \(x^2\) 的分数，求最多可得到多少分数。

注意本题的方块消除后会自动并到一起，和平时玩的消除游戏一样。

想法

区间dp。

首先可以把连续的且颜色相同的方块缩成一段，这和原问题等价。

• \(len_i\) 表示第 \(i\) 段内方块的个数，即它的长度。

• \(id_i\) 表示第 \(i\) 个方块属于哪个段

• \(color_i\) 表示第 \(i\) 个方块段的颜色

大部分人（包括我）第一眼都会设计出这个状态描述：

\(dp[i][j]\) 表示删除 \([i, j]\) 区间内的段最多可得到的得分。

但是很快就会发现这个状态描述是错误的，它无法转移删除后左右两个区间合并的情况。

思路

遇事不决加一维，可以用 \(dp[i][j][k]\) 表示删除 \([i, j]\) 区间内的方块段与 \(j\) 右侧 \(k\) 个颜色与 \(j\) 连续且相同的方块段（不连续就把中间的部分删除），最多可得到的得分。

这样以来就可以转移了。

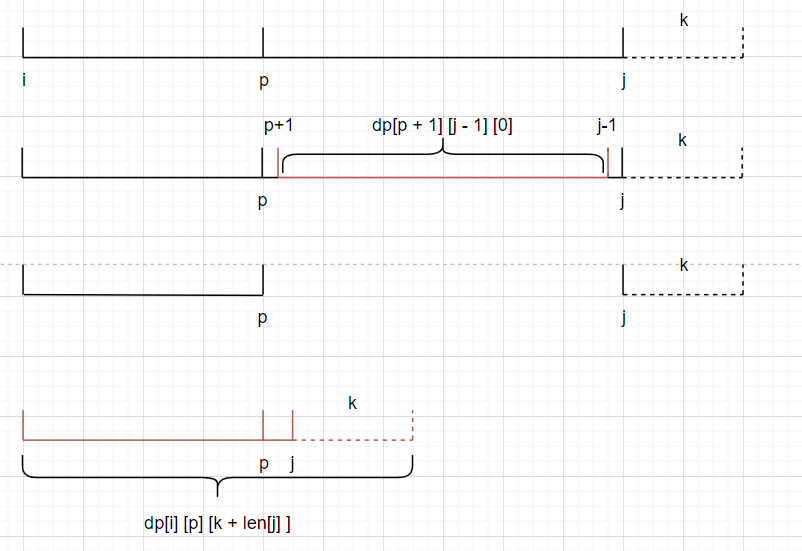
对于任意的状态 \(dp[i][j][k]\)，都有两种决策：

1. 直接删除 \(j\) 这个方块段以及后面 \(k\) 个段并获得得分。

\[dp[i][j - 1][0] + (k + len[j])^2 \]

2. 先合并 \(j\) 方块段和另外一个 \(p\in [i, j)\) 方块段且 \(color_p = color_j\)（不然无意义），再一起删除。

\[dp[i][p][k + len[j]]+ dp[p + 1][j - 1][0] \]

状态数量：\(O(n^3)\)，转移数量：\(O(n)\)，总时间复杂度：\(O(n^4)\)，有点危险，可以使用记忆化搜索实现，这样无用状态不会转移到。

// Problem: 方块消除 Blocks
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA10559
// Memory Limit: 0 MB
// Time Limit: 3000 ms
// Author: Moyou
// Copyright (c) 2022 Moyou All rights reserved.
// Date: 2023-02-03 20:49:20

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <stack>
#include <tuple>
#include <unordered_map>
#define x first
#define y second
#define speedup (ios::sync_with_stdio(0), cin.tie(0), cout.tie(0))
#define INF 0x3f3f3f3f
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;

const int N = 3e2 + 10;

int dp[N][N][N];

int a[N];
int cnt, len[N], id[N], color[N];

int DP(int i, int j, int k)
{
    if(~dp[i][j][k]) return dp[i][j][k];
    dp[i][j][k] = DP(i, j - 1, 0) + (k + len[j]) * (k + len[j]);
    for(int p = i; p < j - 1; p ++)
        if(color[p] == color[j])
        dp[i][j][k] = max(dp[i][j][k], DP(i, p, k + len[j]) + DP(p + 1, j - 1, 0));
    return dp[i][j][k];
}

void work(int i)
{
    memset(dp, -1, sizeof dp);
    memset(len, 0, sizeof len);
    memset(id, 0, sizeof id);
    memset(color, 0, sizeof color);
    memset(a, 0, sizeof a);
    cnt = 0;
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    a[0] = -INF;
    for(int i = 1; i <= n; i ++)
    {
        if(a[i] == a[i - 1])
        {
            id[i] = id[i - 1];
            len[id[i]] ++;
        }
        else
        {
            id[i] = ++ cnt;
            len[id[i]] = 1;
            color[id[i]] = a[i];
        }
    }
    for(int i = 1; i <= cnt; i ++)
        dp[i][i - 1][0] = 0; // basecase
    printf("Case %d: %d\n", i, DP(1, cnt, 0));
}

int main()
{
    int T;
    cin >> T;
    for(int i = 1; i <= T; i ++)
    {
        work(i);
        // puts("");
    }
    // work(T); // uva怎么又换行了（
    

    return 0;
}