虚树学习笔记

如果有这么一个问题：

在一棵超大的，有 \(n\) 个节点树上，并且树上有 \(m\) 个关键点，\(m\) 远小于 \(n\)，如果问题只与关键点有关，我们不能很方便地在这棵超大的树上处理问题，考虑减少冗余。

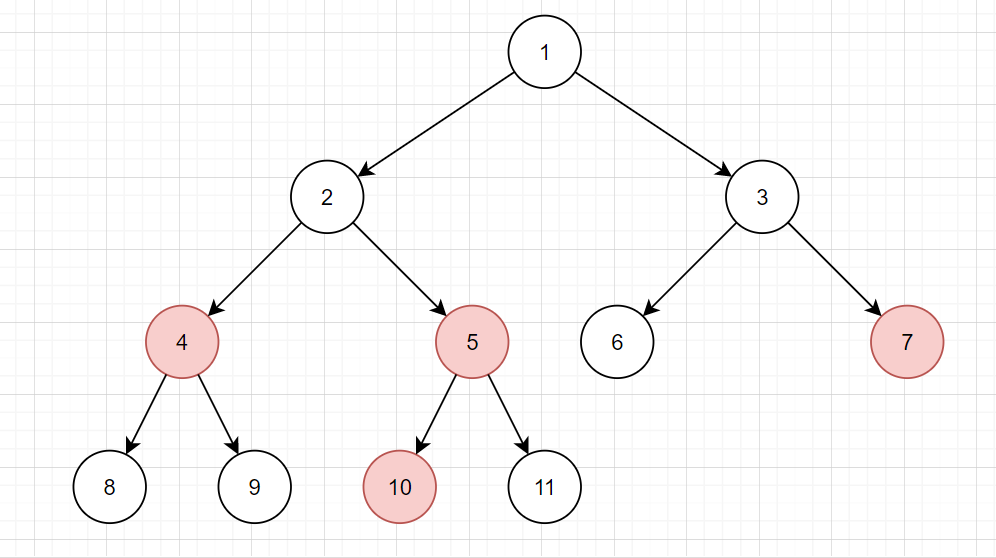
对于这样的一棵树（关键点用红色标注出来了），考虑它的节点中有哪些点对答案有真正的影响。

首先关键点肯定要保留下来，如果只保留关键点，不能很好地表达点之间的关系，为了解决这个问题，可以把关键点之间的 \(\text{LCA}\) 一并保留下来，得到一棵这样的树：

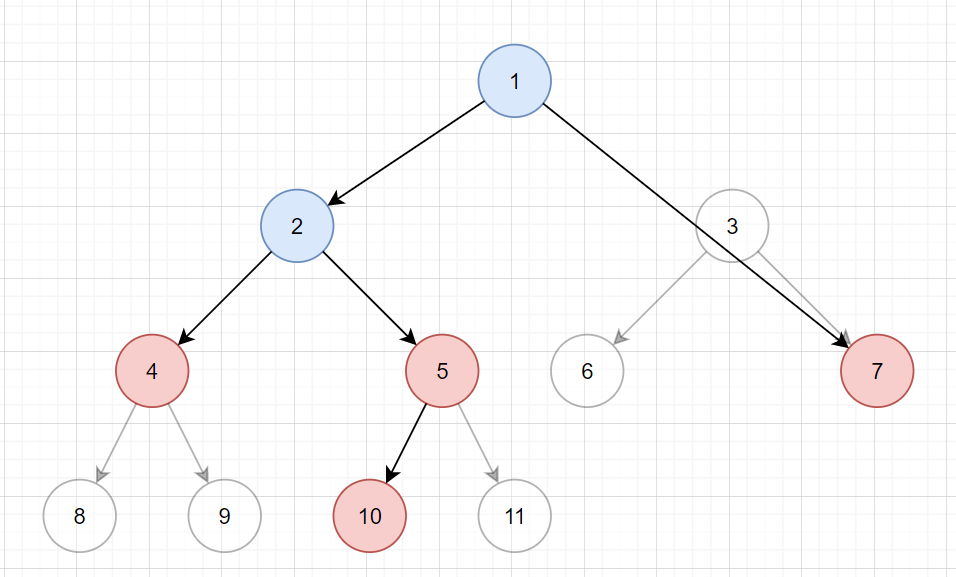
其中蓝色点是关键点的 \(\text{LCAs}\)。

对于这样一棵树，我们称之为虚树，它在保留关键点的祖孙后代关系的前提下，整棵树的点数 \(\le 2m\) 。

构建虚树

如果枚举所有的点对，分别求 \(\text{LCA}\) 这样的时间复杂度显然是平方级别的，不可接受。

可以采用一种名为 Increamental Algorithm 的思想，译为增量算法，在这里的应用类似笛卡尔树的构建，都是维护一条最右链（单调栈）。

把关键点按 \(dfn\) 排序，对于刚刚的例子，得到 4 5 10 7

为了方便，先把 \(1\) 插入单调栈内，接着遍历排序后的数组，进行如下操作：

假设当前遍历到 \(u\)，取出栈顶元素 \(top\)，记栈顶底下的元素 \(stk[top - 1]\) 为 \(top - 1\)，计算 \(lca = \text{LCA(u, top)}\)。
判断 \(dfn[lca]\) 与 \(dfn[top]\)，如果 \(dfn[lca] = dfn[top]\)，意味着 \(lca\) 就是栈顶元素，此时 \(u\) 与栈内元素在同一条链上，不用理这种情况。

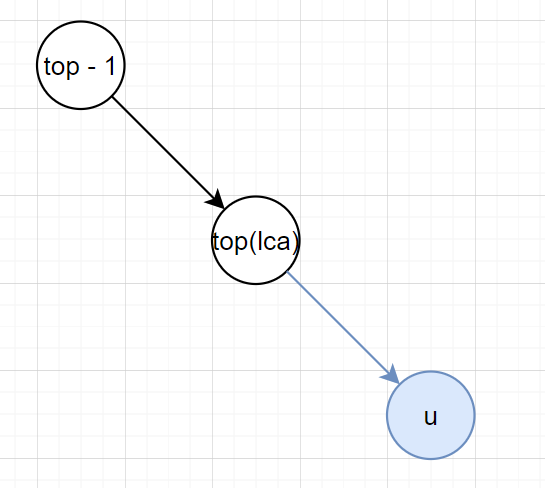
如果 \(dfn[lca] < dfn[top - 1]\)，那么不断弹出栈顶（顺便连接 \(top - 1\) 与 \(top\)，表示这两点一定在虚树内）， \(top\) 与 \(top-1\) 均发生改变，此时有两种情况，图为原树中的子孙关系。

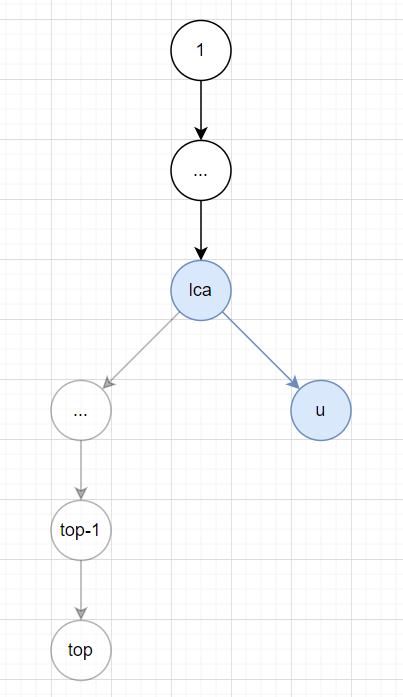
\(lca \ne top - 1(dfn[lca] > dfn[top -1])\)，如下图，此时把 \(top\) 连带着它的儿子们扔到 \(lca\) 左子树中，并把 \(lca\) 代替 \(top\) 成为栈顶。

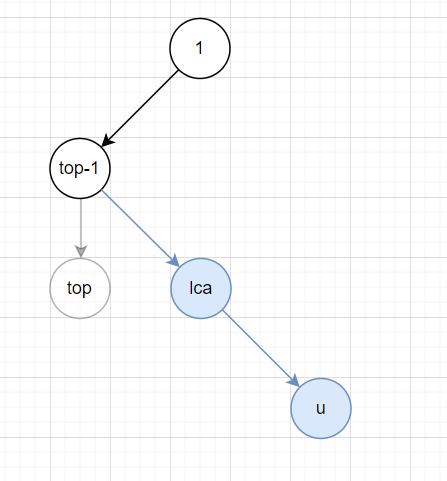
\(lca = top -1(dfn[lca] = dfn[top - 1])\)，类似地，只不过不用把 \(lca\) 压入栈里了。

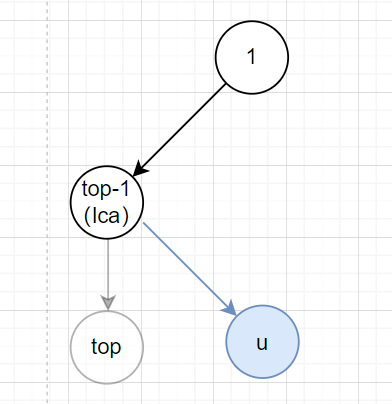
对于上述所有情况，都要记得把 \(u\) 放进最右链（单调栈）。

最后把栈内剩余的元素全部放进虚树（\(top - 1\) 向 \(top\) 连一条边）。

这样就完成了虚树的构建，除了排序的部分，都是线性时间复杂度的。

另有一种建树方法，将所有关键点按 \(dfn\) 排序，然后求出相邻的边的 \(\text{LCA}\)，最后把所有关键点和 \(\text{LCAs}\) 去重，然后重新按 \(dfn\) 排序，连接 \(lca(i, i - 1), i\)，即可求出虚树。

int tot;
void build2()
{
    sort(imp + 1, imp + k + 1, cmp);
    tot = k; // 全部加入序列
    for(int i = 2; i <= k; i ++)
    {
        int lca = LCA(imp[i], imp[i - 1]);
        if(lca != imp[i] && lca != imp[i - 1]) imp[++ tot] = lca; // lca也加入
    }
    sort(imp + 1, imp + tot + 1);
    tot = unique(imp + 1, imp + tot + 1) - imp - 1; // 去重
    sort(imp + 1, imp + tot + 1, cmp);
    
    for(int i = 2, lca; i <= tot; i ++) // 连边
        lca = LCA(imp[i], imp[i - 1]), vadd(lca, imp[i]);
}

不过时间复杂度都是 \(O(k\log k) \sim O(k\log k \log n)\)

建树之后

对于 [SDOI2011] 消耗战，有一个显然的树形dp：

\(dp[i]\) 表示以 \(i\) 为根的子树中，删掉所有关键点所需的最小花费。

预处理 \(minv[i]\)，表示 \(i\) 到 \(1\) 的最短边长。

\(i\) 是关键点，\(dp[i] = minv[i]\)
\(i\) 不是关键点，\(dp[i] = min(minv[i], \sum_{(i, v, w)\in E}w_i)\)

在虚树上跑一遍 dp 就好了，如果用 RMQ ST 实现 LCA 时间复杂度：\(O(n\log n + \sum (k\log k))\)

// Problem: P2495 [SDOI2011] 消耗战
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2495
// Memory Limit: 505 MB
// Time Limit: 2000 ms
// Author: Moyou
// Copyright (c) 2022 Moyou All rights reserved.
// Date: 2023-01-31 18:13:24

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#define int long long
#define speedup (ios::sync_with_stdio(0), cin.tie(0), cout.tie(0))
#define INF 0x3f3f3f3f
using namespace std
typedef pair<int, int> PII;

const int N = 2e5 + 10;

vector<PII> g[N];

struct STLCA
{
    int pos[N], idx, dfn[(N << 1) + 10];
    int st[21][(N << 1) + 10], lg[(N << 1) + 10];
    void dfs(int p, int fa)
    {
        dfn[++idx] = p;
        pos[p] = idx;
        for (auto [v, w] : g[p])
        {
            if (v == fa)
                continue;
            dfs(v, p);
            dfn[++idx] = p;
        }
    }

    int Min(int a, int b)
    {
        return pos[a] < pos[b] ? a : b;
    }
    void ST()
    {
        lg[1] = 0;
        for (int i = 2; i <= (N << 1); i++)
            lg[i] = lg[i >> 1] + 1;
        for (int i = 1; i <= (N << 1); i++)
            st[0][i] = dfn[i];
        for (int i = 1; i <= lg[(N << 1) - 1]; i++)
            for (int j = 1; j + (1 << i) <= (N << 1); j++)
                st[i][j] = Min(st[i - 1][j], st[i - 1][j + (1 << i - 1)]);
    }

    int LCA(int u, int v)
    {
        int l = pos[u], r = pos[v];
        if (l > r)
            swap(l, r);
        int k = lg[r - l + 1];
        return Min(st[k][l], st[k][r - (1 << k) + 1]);
    }
} st;

int dp[N], dfn[N], cnt;
int imp[N];
bool is[N];
int k;
int minv[N];

void dfs(int u, int fa)
{
    dfn[u] = ++cnt;
    for (auto [v, w] : g[u])
    {
        if (v == fa)
            continue;
        minv[v] = min(minv[u], w);
        dfs(v, u);
    }
}

vector<int> vir[N];

void add(int a, int b)
{
    vir[a].push_back(b);
}

int Dp(int u, int fa)
{
    int sum = 0;
    for (auto v : vir[u])
        sum += Dp(v, u);
    int ans = INF;
    vir[u].clear();
    if(is[u]) 
        ans = minv[u];
    else ans = min(minv[u], sum);
    is[u] = false;
    return ans;
}

int n;
int bucket[N];
void build()
{
    sort(imp + 1, imp + k + 1, [](int a, int b) { return dfn[a] < dfn[b]; });
    int stk[N], top = 0;
    stk[++top] = 1; // 显然多增加点不影响正确性，为了方便就加入1
    for (int i = 1; i <= k; i++)
    {
        if (imp[i] == 1) // 防止重复入栈
            continue;
        int lca = st.LCA(stk[top], imp[i]);
        if(lca != stk[top])
        {
            while (dfn[lca] < dfn[stk[top - 1]])
                add(stk[top - 1], stk[top]), top --;
            if (lca != stk[top - 1])
                add(lca, stk[top]), stk[top] = lca;
            else
                add(lca, stk[top--]);
        }
        stk[++top] = imp[i];
    }

    for (int i = 1; i < top; i++) // 栈内剩余全部连边
        add(stk[i], stk[i + 1]);
}

signed main()
{
    speedup;
    cin >> n;
    memset(minv, 0x7f, sizeof minv);
    for (int i = 1; i < n; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a].push_back({b, c}), g[b].push_back({a, c});
    }

    dfs(1, 0);
    st.dfs(1, 0);
    st.ST();

    int m;
    cin >> m;
    for (int i = 1; i <= m; i++)
    {
        cin >> k;
        for (int j = 1; j <= k; j++)
            cin >> imp[j], is[imp[j]] = true;
        build();
        cout << Dp(1, 0) << "\n";
    }

    return 0;
}

posted @ 2023-02-01 18:21 MoyouSayuki 阅读(84) 评论(0) 编辑收藏举报

刷新页面返回顶部

MoyouSayuki

虚树 学习笔记

虚树 学习笔记

构建虚树

建树之后

公告

虚树学习笔记

虚树学习笔记