[CF380C] Sereja and Brackets 题解

[CF380C] Sereja and Brackets 题解

给定一个括号串 \(s\) 与 \(m\) 次询问。

• l, r 回答字符串 \(t = s_ls_{l+1}\dots s_r\)​ 的所有子序列中最长的合法括号串的长度。

\(1\le |s|\le 10^6\)，\(1\le m\le 10^5\)

想法

对于括号序列有一种数形结合的 trick，即把 ( 记为 1，) 记为 -1，并记录它们的前缀和。

例如样例可以转换为 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1

它的前缀和为 1 0 -1 0 1 0 -1 0 1 0 -1 0

把它拍到折线统计图上

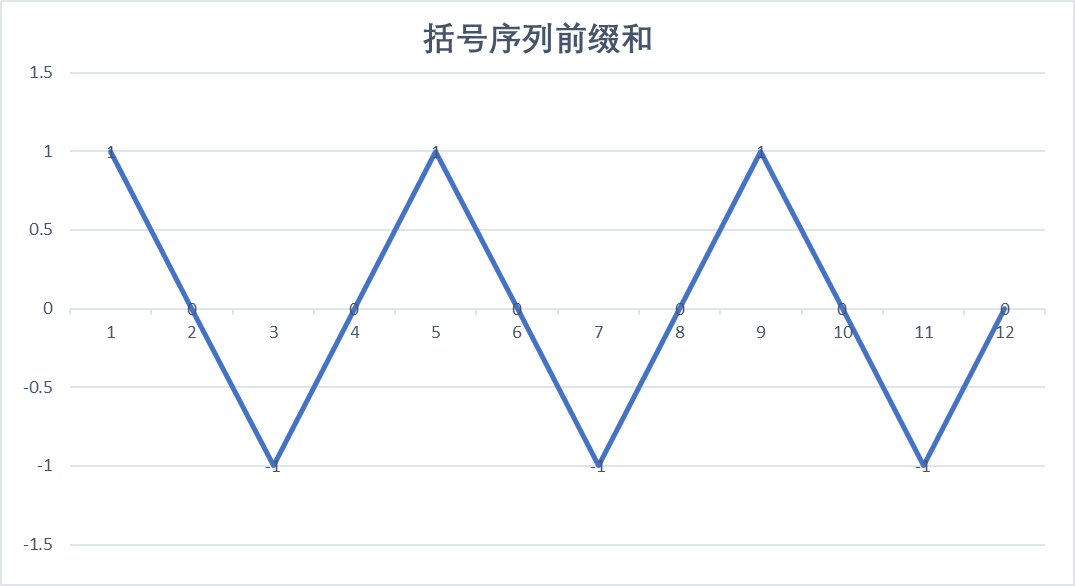
记 \(h_i\) 为 \(i\) 的前缀和。

观察发现一个合法括号序列区间 [l, r] 一定满足：

1. \(\forall i\in[l, r], h_i \geq h_l\)，即 \(l\) 是区间的最低点。
2. \(h_r = h_l\)，即区间的结尾一定与区间的开头高度相等。

于是只需要统计区间内这些区间的长度即可，不妨反向考虑整个问题。

设区间长度为 \(len\)，最低点高度为 \(minp\)。

则区间中未匹配的左括号数量为：\(|h_l - minp|\)；

区间中未匹配的右括号数量为：\(|h_r - minp|\)

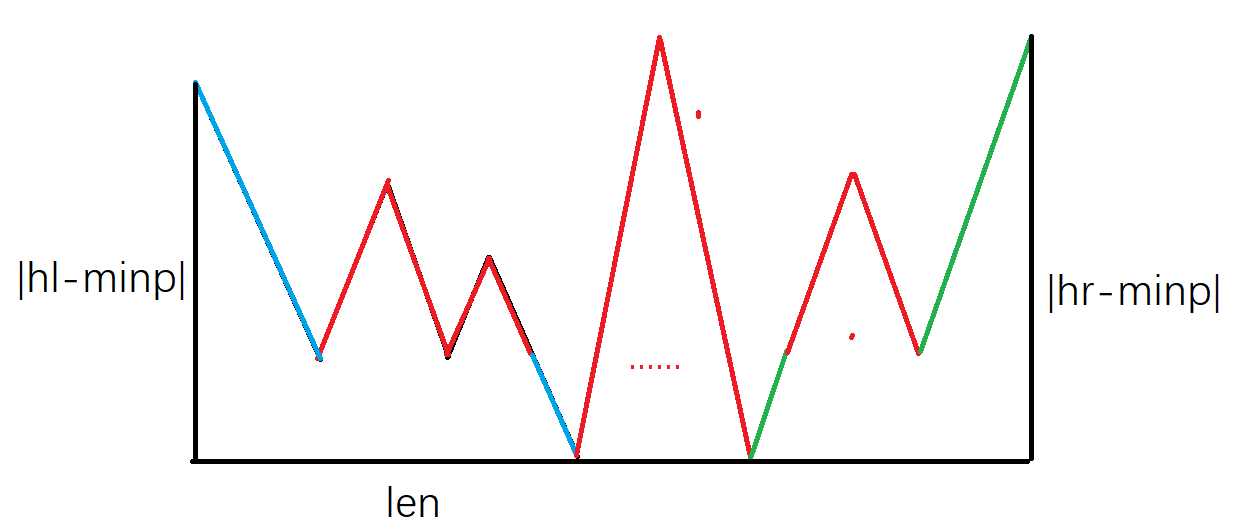
因此答案为 \(len - |h_l - minp| - |h_r - minp|\)。

只需要求出 \(minp\) 整个问题就解决了。

可以用线段树 / ST表解决这个 RMQ 问题。

实现

我采用了线段树，时间复杂度：\(O(m\log n)\)

代码实现中需要一些边界判断。

// Problem: Sereja and Brackets
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF380C
// Memory Limit: 250 MB
// Time Limit: 1000 ms
// Author: Moyou
// Copyright (c) 2022 Moyou All rights reserved.
// Date: 2023-01-28 22:36:03

#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
#define speedup (ios::sync_with_stdio(0), cin.tie(0), cout.tie(0))
#define INF 0x3f3f3f3f
using namespace std;

const int N = 1e6 + 10;

int h[N];

void init(string s)
{
    for (int i = 0; i < s.size(); i++)
        h[i] = (i - 1 >= 0 ? h[i - 1] : 0) + (s[i] == '(' ? 1 : -1);
    for(int i = s.size(); i; i --)
        h[i] = h[i - 1];
    h[0] = 0;
}

int n;
string s;

struct owo
{
    int l, r, dat;
} tr[N << 2];

void build(int k, int l, int r)
{
    tr[k].l = l, tr[k].r = r;
    if (l == r)
        tr[k].dat = h[l];
    else
    {
        int mid = l + r >> 1;
        build(k << 1, l, mid);
        build(k << 1 | 1, mid + 1, r);
        tr[k].dat = min(tr[k << 1].dat, tr[k << 1 | 1].dat);
    }
}

int query(int k, int ql, int qr)
{
    int l = tr[k].l, r = tr[k].r, mid = l + r >> 1;
    if (ql <= l && qr >= r)
        return tr[k].dat;
    int t = INF;
    if (ql <= mid)
        t = query(k << 1, ql, qr);
    if (qr > mid)
        t = min(t, query(k << 1 | 1, ql, qr));
    return t;
}

int main()
{
    speedup;
    cin >> s >> n;
    init(s), build(1, 1, s.size());

    for (int i = 1; i <= n; i++)
    {
        int l, r;
        cin >> l >> r;
        int len = r - l + 1;
        int minp = query(1, l, r);
            int a = abs(h[l - 1] - minp), b = abs(h[r] - minp);
        cout << len - a - b << endl;
    }

    return 0;
}