RMQ CLA

用 ST 算法解决 LCA 问题

本文介绍一种可以在 \(O(n\log n)\) 时间内预处理，\(O(1)\) 查询 \(\text{LCA}\) 的算法。

欧拉序

\(\text{DFS}\) 一棵树，将到达的节点与回溯到的节点的编号按顺序记录下来，得到的序列称为欧拉序。

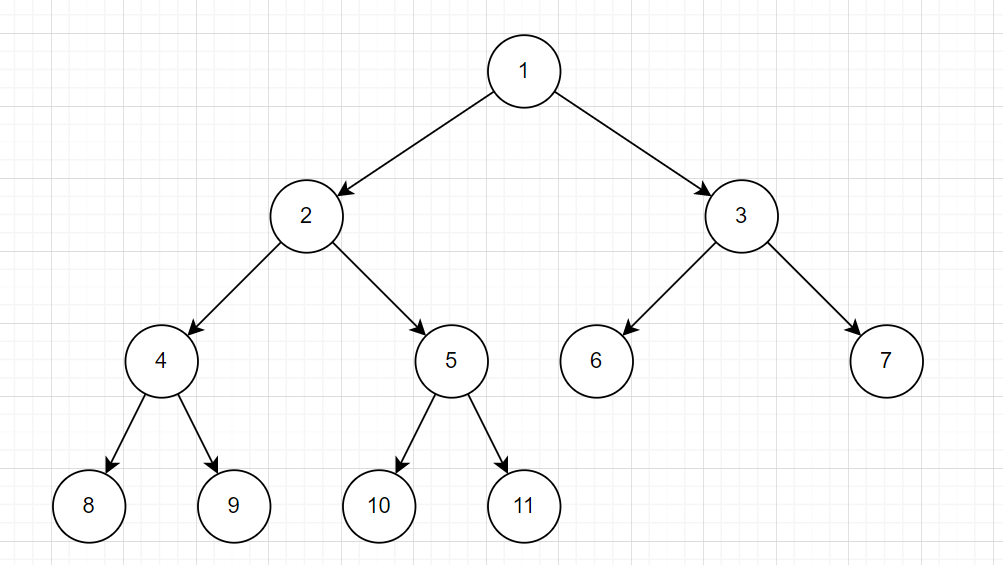
对于这棵树而言，它的欧拉序是：

\[\color{red}{1}\rightarrow 2\rightarrow 4\rightarrow 8\rightarrow \color{blue}4\rightarrow \color{red}9\rightarrow \color{blue}4\rightarrow 2\rightarrow \color{red}5\rightarrow \\\color{red}10\color{blue}\rightarrow 5\rightarrow\color{red} 11\rightarrow \color{blue}5\rightarrow 2\rightarrow 1\rightarrow \color{red}3\rightarrow 6\rightarrow \color{blue}3\rightarrow \color{red}7\rightarrow \color{blue}3\rightarrow 1 \]

我们用 \(dfn\) 数组记录欧拉序，其中红色表示这个节点是第一次被访问，蓝色表示这个节点是回溯后被访问到的。

从 \(\text{LCA}\) 到 \(\text{RMQ}\)

我们用 \(pos_i\) 表示节点 \(i\) 的欧拉序，即第一次访问到 \(i\) 时它在欧拉序中下标，例如 \(pos_4 = 3,pos_9=6\)。

注意到欧拉序有一个很强的性质——对于任意两个欧拉序中红色的元素 \(l, r\)，他们之间的元素包含 \(\text{LCA}(l,r)\) 并且不会包含其他公共祖先。

一旦包含了其他公共祖先，就说明以 \(\text{LCA}\) 为根的子树已经遍历完毕，然而此时 \(r\) 并未被遍历到。

而 \(dfn_l \sim dfn_r\)中深度 / 欧拉序最小的显然就是 \(\text{LCA}(l, r)\)。

由此我们完成了 \(\text{LCA}\) 问题到 \(\text{RMQ}\) 问题的转化，从求 \(\text{LCA(u, v)}\) 到求 \(\min\limits_{i=l}^r(pos_i)\)。

这里使用 \(\text{ST}\) 表解决这个问题。

时间复杂度：\(O(n\log n)\) 预处理 \(O(1)\) 查询。

实现

实现上 \(\text{ST}\) 表需要做出一个小变化，不记录元素的值，而记录元素的下标。

1. 一遍 \(\text{DFS}\) 预处理出 \(dfn\) 与 \(pos\) 数组。
2. \(\text{ST}\) 表预处理
3. 询问 \(O(1)\) 回答

int pos[N], idx, dfn[N];
int st[21][N], lg[N << 1];
void dfs(int p, int fa)
{
    dfn[++idx] = p;
    pos[p] = idx;
    for (auto i : g[p])
    {
        if (i == fa)
            continue;
        dfs(i, p);
        dfn[++idx] = p;
    }
}

int Min(int a, int b) { return pos[a] < pos[b] ? a : b; }
void ST()
{
    lg[1] = 0;
    for (int i = 2; i <= N; i++)
        lg[i] = lg[i >> 1] + 1;
    for (int i = 1; i <= N - 1; i++)
        st[0][i] = dfn[i];
    for (int i = 1; i <= lg[N - 1]; i++)
        for (int j = 1; j + (1 << i) <= N; j++)
            st[i][j] = Min(st[i - 1][j], st[i - 1][j + (1 << i - 1)]);
}

int RMQ(int l, int r)
{
    int k = lg[r - l + 1];
    return Min(st[k][l], st[k][r - (1 << k) + 1]);
}

板子题：P3379

其实可以用 \(\pm\) RMQ 和四毛子 优化到 \(O(n)\) 预处理，不过实现太麻烦了，而且常数也很大，对于 \(OIer\) 来说性价比比较低。