[POI2004]WYS 题解 扫描线算法

[POI2004]WYS 题解

P4633

奇怪的题目名。

题目描述

给 \(n\) 个互不相交的多边形，这些多边形的边均平行或垂直于坐标轴。定义多边形 \(i\) 的深度 \(d_i\) 为 \(\max\{d_j\}+1\)，其中多边形 \(j\) 包含多边形 \(i\)。特别的，若一个多边形不被任何多边形包含，则其深度为 \(1\)。求深度最大的多边形的深度。\(n \leqslant 40000\)。

思路

扫描线 算法。

假装有一条线，平行于 y 轴，从左往右扫描整个图形，那么整个图形就会被分割为几个长条。

长条内部同一 y 坐标的部分深度一定相同，这样只需要知道所有长条内部区间的深度即可解决这个问题。

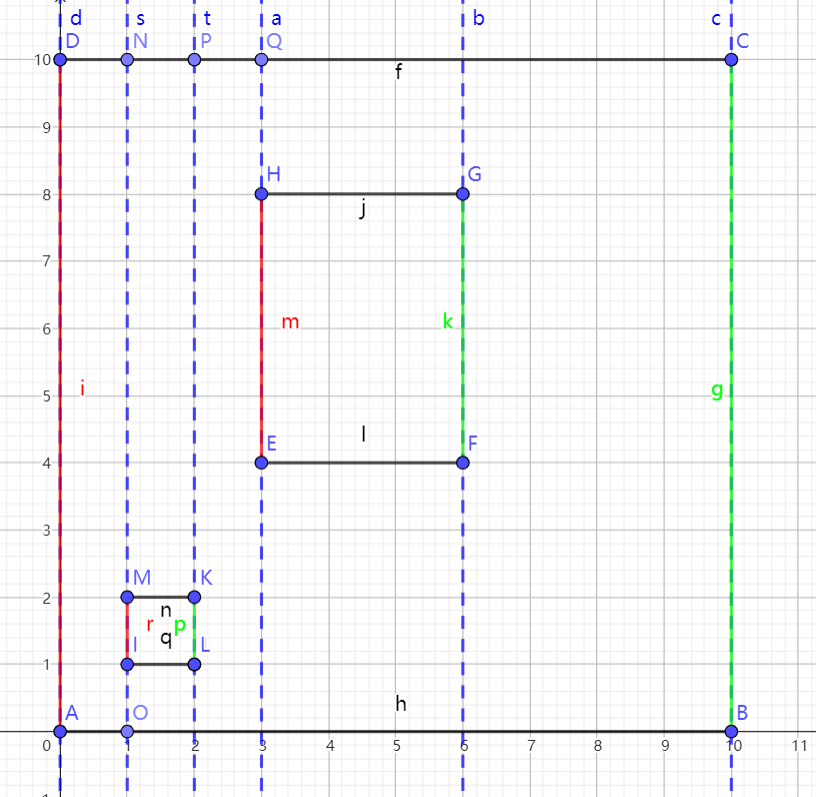
可以发现，只要这条扫描线经过了一个多边形的左边界（即红色的线段），那么这条线段就会对它所代表的 y 坐标区间产生 \(1\) 个深度贡献，代表这个区间新被一个多边形所覆盖。

对应地，当扫描线经过多边形的右边界（即绿色的线段），这条线段所代表的 y 坐标区间会产生 \(-1\) 的深度贡献，代表这个区间不再被一个多边形所覆盖。

其中多边形左边界的定义是：在这条线段左侧都不属于此多边形而线段右侧都属于此多边形。右边界同理。

我们可以使用 线段树 维护这个区间深度信息。

另外，由于题目数据范围比较大，需要离 离散化。

代码

// Problem: P4633 [POI2004]WYS
// URL: https://www.luogu.com.cn/problem/P4633
// Author: Moyou
// Copyright (c) 2022 Moyou All rights reserved.
// Date: 2023-01-10 11:16:33

#include <algorithm>
#include <iostream>
#define INF 0x3f3f3f3f
using namespace std;

const int N = 1e4 + 10, M = 4e5 + 10; // 空间不要钱

int x[N];
struct edge
{
    int x, l, r;
    int pl;
} e[M];
int b[M], nn, n;
int idx;

int ans = -INF;
int dat[M], tag[M];

void down(int k, int l, int r) // 懒标记下沉
{
    tag[k << 1] += tag[k], tag[k << 1 | 1] += tag[k];
    dat[k << 1] += tag[k], dat[k << 1 | 1] += tag[k];
    tag[k] = 0;
}

void update(int a, int b, int k, int l, int r, int x) // 更新区间深度信息
{
    if (b <= l || a >= r)
        return;
    if (a <= l && r <= b)
    {
        tag[k] += x;
        dat[k] += x;
        return;
    }
    if (tag[k])
        down(k, l, r);
    update(a, b, k << 1, l, l + r >> 1, x);
    update(a, b, k << 1 | 1, l + r >> 1, r, x);
    dat[k] = min(dat[k << 1], dat[k << 1 | 1]);
}

int query(int a, int b, int k, int l, int r) // 查询深度信息
{
    if (b <= l || a >= r)
        return INF;
    if (a <= l && r <= b)
        return dat[k];
    if (tag[k])
        down(k, l, r);
    return min(query(a, b, k * 2, l, l + r >> 1), query(a, b, k * 2 + 1, l + r >> 1, r));
}

int main()
{
    int tmp;
    cin >> tmp;
    for (int i = 1; i <= tmp; i++) // 读入多边形
    {
        int k;
        cin >> k;
        for (int j = 1; j <= k; j++)
            cin >> x[j], b[++n] = x[j];
        for (int j = 1; j <= k - 2; j++)
            if (j % 2 == 0) // 题目中说了，边是逆时针给出的，因此向下的边一定是右边界，左边界反之
            {
                if (x[j + 2] > x[j]) // 一条往下的边，是右边界
                    e[++idx] = {x[j + 1], x[j], x[j + 2], -1};
                else // 一条往上的边，是左边界
                    e[++idx] = {x[j + 1], x[j + 2], x[j], 1};
            }
        if (x[k] > x[2]) // 一条往上的边，是左边界
            e[++idx] = {x[1], x[2], x[k], 1};
        else // 一条往下的边，是右边界
            e[++idx] = {x[1], x[k], x[2], -1};
    }
    sort(b + 1, b + n + 1); // 离散化
    sort(e + 1, e + idx + 1, [](edge a, edge b) { return a.x < b.x; }); // 确定扫描的顺序
    n = unique(b + 1, b + n + 1) - b;
    while ((1 << nn) <= n)
        nn++;
    nn = 1 << nn; // 线段树有2^k的节点的话比较方便
    for (int i = 1; i <= idx; i++)
    {
        int l = lower_bound(b + 1, b + n + 1, e[i].l) - b;
        int r = lower_bound(b + 1, b + n + 1, e[i].r) - b;
        update(l, r + 1, 1, 1, nn + 1, e[i].pl);
        ans = max(ans, query(l, r + 1, 1, 1, nn + 1)); // 更新答案
    }
    cout << ans << endl;

    return 0;
}