浅析次小生成树

次小生成树

思路

以下称 “在最小生成树内部的边” 为树边，非树边反之。

结论：次小生成树和最小生成树有且仅有一边之差。

次小生成树有两种求法：

1. 建立最小生成树，从树边的角度考虑，如果我们删掉一条最小生成树内部的边，再在没有这条边的图上做最小生成树，这样做出来的生成树一定是（非严格）次小生成树。
   时间复杂度：\(O(m\log m(最小生成树) + nm(删边后的最小生成树))\)，由于已经做过排序了，所以删边后的最小生成树就不需要排序了。
2. 建立最小生成树，从非树边的角度考虑，如果我们加入一条非树边，此时最小生成树会变为一棵基环树，只要在这个环上删掉任意一条树边就可以构成一个新的生成树.
   新的生成树的边权和为：

\[原边权和-删掉的边权+新加入的边权 \]

为了得到次小生成树，要使新边权和最小，也就要求 \(删掉的边权\) 最大，这个可以用很多方法处理出来，可以证明，次小生成树一定在新生成树的集合内，只需要在新生成树构成的集合中取边权和最小的即可，严格次小生成树还要求边权和与最小生成树不相等。

方法1扩展性不强，很难求严格次小生成树，因此这里采用方法2实现。

非严格次小生成树

Code

#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>
#define v first
#define w second
using namespace std;
typedef pair<int, int> PII;

const int N = 510, M = 1e4 + 10;
struct qwq
{
    int a, b, c, id;
} e[M];

int fa[N];
int find(int x)
{
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

vector<PII> g[N];

int mxw[N][N];
int n, m;

void dfs(int ac, int p, int fa, int mx)
{
    for (auto [j, c] : g[p])
    {
        if (j == fa)
            continue;
        mxw[ac][j] = max(mx, c);
        dfs(ac, j, p, max(mx, c));
    }
}

void init()
{
    for (int i = 1; i <= n; i++)
    {
        dfs(i, i, -1, -1);
    }
}

bool is_tree[M];
int ans = 0, sum = 0;

void kruskal()
{
    for (int i = 1; i <= n; i++)
        fa[i] = i;
    sort(e + 1, e + m + 1, [](qwq a, qwq b) { return a.c < b.c; });

    int cnt = 1, i = 0;
    for (auto [a, b, c, id] : e)
    {
        i++;
        int x = find(a), y = find(b);
        if (x == y)
            continue;
        fa[x] = y;
        sum += c;
        g[a].push_back({b, c});
        g[b].push_back({a, c});
        cnt++;
        is_tree[id] = true;
    };
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        e[i] = {a, b, c, i};
    }
    kruskal();
    init();
    ans = 0x3f3f3f3f;
    for (int i = 1; i <= m; i++)
    {
        if (is_tree[e[i].id])
            continue;
        ans = min(ans, sum + e[i].c - mxw[e[i].a][e[i].b]);
    }

    cout << ans << endl;
    return 0;
}

严格次小生成树

与非严的唯一区别在于需要记录一个次大边权，这样可以在最大边权相同的时候有一个退路。

时间复杂度：\(O(m\log m + n^2)\)

Code

#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>
#define v first
#define w second
#define int long long
using namespace std;
typedef pair<int, int> PII;

const int N = 510, M = 1e4 + 10;
struct qwq
{
    int a, b, c, id;
} e[M];

int fa[N];
int find(int x)
{
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

vector<PII> g[N];

int mxw[N][N], mx2w[N][N];
int n, m;

void dfs(int ac, int p, int fa, int mx, int mx2)
{
    for (auto [j, c] : g[p])
    {
        if (j == fa)
            continue;
        int t1 = mx, t2 = mx2;
        if (c > t1)
            t2 = t1, t1 = c;
        else if (c != t1 && c > t2)
            t2 = c;
        mxw[ac][j] = t1;
        mx2w[ac][j] = t2;
        dfs(ac, j, p, t1, t2);
    }
}

void init()
{
    for (int i = 1; i <= n; i++)
    {
        dfs(i, i, -1, -1, -1);
    }
}

bool is_tree[M];
int ans = 0, sum = 0;

void kruskal()
{
    for (int i = 1; i <= n; i++)
        fa[i] = i;
    sort(e + 1, e + m + 1, [](qwq a, qwq b) { return a.c < b.c; });

    int i = 0;
    for (auto [a, b, c, id] : e)
    {
        i ++;
        int x = find(a), y = find(b);
        if (x == y)
            continue;
        fa[x] = y;
        sum += c;
        g[a].push_back({b, c});
        g[b].push_back({a, c});
        is_tree[id] = true;
    };
}

signed main()
{
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        e[i] = {a, b, c, i};
    }
    kruskal();
    init();
    ans = 1e18;
    for (int i = 1; i <= m; i++)
    {
        if (is_tree[e[i].id])
            continue;
        if (e[i].c == mxw[e[i].a][e[i].b])
            ans = min(ans, sum + e[i].c - mx2w[e[i].a][e[i].b]);
        else
            ans = min(ans, sum + e[i].c - mxw[e[i].a][e[i].b]);
    }

    cout << ans << endl;
    return 0;
}

优化

上述代码只能在 [BJWC2010] 严格次小生成树 中得到 \(50\) 分，考虑优化。

如果使用 \(\text{Dfs}\) 处理两点之间的最大边权，时间复杂度为 \(O(n^2)\) 不能接受。

这个树上问题可以采用树剖/动态树/LCA等多种方法解决，由于我是蒟蒻只会 LCA，所以这里暂时只介绍LCA的优化方式。

\(mx1[j][i]\) 表示 \(j\) 到它的 \(2^i\) 级祖先路径上的最大权值，则有：

\[令anc = f[j][i - 1]\\ mx1[j][i] = \max(mx1[j][i - 1], mx1[anc][i - 1]) \]

由于是严格次小生成树，因此还需要要维护一个次大权值。

\(mx2[j][i]\) 表示 \(j\) 到它的 \(2^i\) 级祖先路径上的次大权值，则有：

\[令t=\min(mx1[j][i - 1], mx1[anc][i - 1])\\ mx2[j][i] = \max(t, mx2[j][i - 1], mx2[anc][i - 1]) \]

注意，当 \(mx1[j][i - 1] = mx1[anc][i - 1]\) 时，下式应忽略 \(t\)，读者可以思考一下为什么。

由于是一棵树，因此任意点 \(a\rightarrow b\) 的路径一定可以被拆分为一下两段。

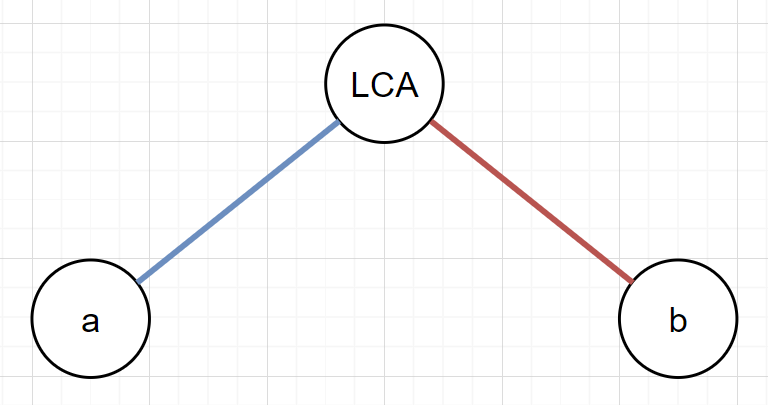
所以最终的 \(a\rightarrow b\) 的路径最大权值就可以表示为 \(\max(w_1, w_2)\)，其中 \(w_1, w_2\) 分别表示蓝色段的最大权值、红色段的最大权值，分别用二进制枚举处理处理即可。

理论时间复杂度：\(O(m\log m + n\log n)\)。

// Problem: P4180 [BJWC2010] 严格次小生成树
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4180
// Memory Limit: 500 MB
// Time Limit: 1000 ms
// Author: Moyou
// Copyright (c) 2022 Moyou All rights reserved.
// Date: 2023-01-05 13:32:13

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#define int long long
#define INF 1e18
using namespace std;
typedef pair<int, int> PII;

const int N = 1e5 + 10, M = 6e5 + 10;

struct qwq
{
    int a, b, c;
    bool is;
} e[M];

int fa[N], n, m;
int find(int x)
{
    return x == fa[x] ? x : fa[x] = find(fa[x]);
}

int sumt;
vector<PII> g[N];

void kruskal()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        fa[i] = i;
    for (int i = 1; i <= m; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        e[i] = {a, b, c, 0};
    }
    sort(e + 1, e + m + 1, [](qwq a, qwq b) { return a.c < b.c; });
    for (int i = 1; i <= m; i++)
    {
        int x = find(e[i].a), y = find(e[i].b);
        if (x == y)
            continue;
        fa[x] = y;
        sumt += e[i].c;
        g[e[i].a].push_back({e[i].b, e[i].c});
        g[e[i].b].push_back({e[i].a, e[i].c});
        e[i].is = true;
    }
}

int depth[N], f[N][25], mx1[N][25], mx2[N][25];
void get_depth(int u, int fa, int w)
{
    depth[u] = depth[fa] + 1;
    f[u][0] = fa;
    mx1[u][0] = w;
    for (int i = 1; i <= 20; i++)
    {
        f[u][i] = f[f[u][i - 1]][i - 1];                         // 更新f倍增数组
        mx1[u][i] = max(mx1[u][i - 1], mx1[f[u][i - 1]][i - 1]); // 路径最大值
        int t = min(mx1[u][i - 1], mx1[f[u][i - 1]][i - 1]);
        if (mx1[u][i - 1] == mx1[f[u][i - 1]][i - 1]) 
            // 如果路径上最大权值相等的话，次大值就有可能与最大值相等
            t = 0;
        mx2[u][i] = max({t, mx2[u][i - 1], mx2[f[u][i - 1]][i - 1]}); // 路径次大值
    }

    for (auto [j, c] : g[u])
    {
        if (j == fa)
            continue;
        get_depth(j, u, c);
    }
    return;
}

int lca(int a, int b) // 板
{
    if (depth[a] > depth[b])
        swap(a, b);
    for (int i = 20; i >= 0; i--)
        if (depth[f[b][i]] >= depth[a])
            b = f[b][i];
    if (a == b)
        return a;
    for (int i = 20; i >= 0; i--)
    {
        if (f[a][i] != f[b][i])
        {
            a = f[a][i];
            b = f[b][i];
        }
    }
    return f[a][0];
}

int get_mx(int a, int b, int c) // 求 a 到 b 路径上的不与 c 相等的最大权值
{
    int res = -INF;
    for (int i = 20; i >= 0; i--)
    {
        if (depth[f[a][i]] >= depth[b])
        {
            if (c == mx1[a][i])
                res = max(res, mx2[a][i]);
            else
                res = max(res, mx1[a][i]);
            a = f[a][i];
        }
    }
    return res;
}

int ans = INF;
void work()
{
    for (int i = 1; i <= m; i++)
    {
        if (e[i].is)
            continue;
        int ancient = lca(e[i].a, e[i].b);
        int t1 = get_mx(e[i].a, ancient, e[i].c); // a 到 b 路径上的最大权值即为 max()
        t1 = max(t1, get_mx(e[i].b, ancient, e[i].c));
        ans = min({ans, sumt + e[i].c - t1});
    }
    cout << ans << '\n';
}

signed main()
{
    kruskal();
    get_depth(1, 0, 0);
    work();
    return 0;
}

非严次小同理。