Kruskal重构树 学习笔记
最小/大瓶颈路
在探究何为 \(\text{Kruskal}\) 重构树之前,我们先要了解何为最小/大瓶颈路。
简单来说,\(a\) 到 \(b\) 的最小瓶颈路指的是一条简单路径使得 \(a\) 到 \(b\) 的最大边权最小,最大瓶颈路反之。
定义
\(\text{Kruskal}\) 重构树是如此构建的,类似 \(\text{Kruskal}\) 算法的过程:
- 对所有边进行排序
- 从小到大(此处只讨论最小瓶颈路,最大瓶颈路同理)枚举所有边。
- 如果此边连接的两点在同一集合中,那么跳过这条边。
- 如果此边连接的两点 \(a, b\) 不在同一集合中,那么把这个边权 “提起来” 使它成为一个新建虚点的点权,此虚点两个子节点分别为 \(a, b\) 所在的集合。
- 不断迭代步骤 \(2\) 直到所有边被遍历完。
由此得到了一棵 \(\text{Kruskal}\) 重构树。
可以来模拟一下过程:
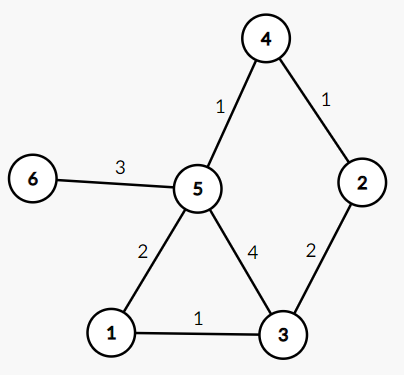
如果有这么一张图,对它构建 \(\text{Kruskal}\) 重构树,过程如下:
-
排序:
排序好的的边 \((u, v, w)\) 如下:\(\color{red}{(1, 3, 1), (2, 4, 1), (4, 5, 1)}, \color{orange}{(1, 5, 2), (2, 3, 2)},\color{green} (5, 6, 3),\color{blue} (3, 5, 4)\)(边权相同的边已用相同颜色标注)。
-
从小到大枚举所有边:
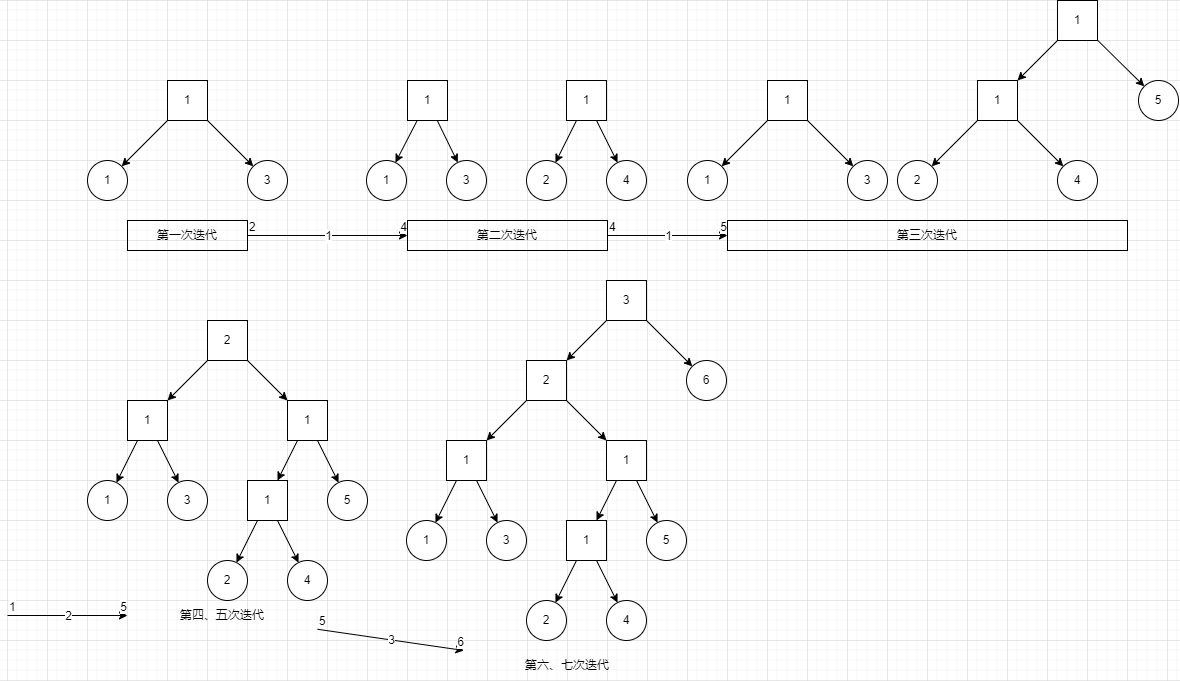
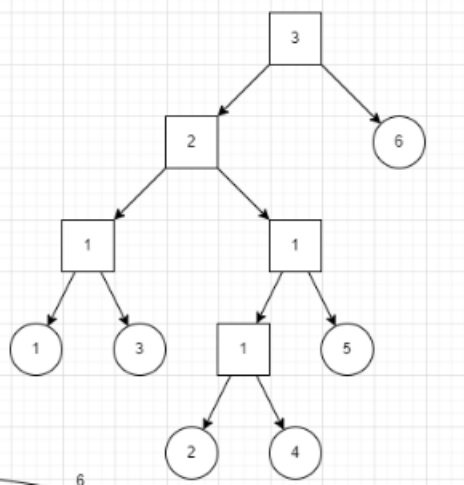
得到最后的重构树。
性质
\(\text{Kruskal}\) 重构树中的方节点的权值可以这么理解:
如果令方节点为 \(p\),点权为 \(w\),两个子树中圆节点组成的集合为 \(S_{left}\) 与 \(S_{right}\)。定义集合 \(A, B\) 的距离为 \(dist[A][B]\),表示 \(A\) 中所有点到 \(B\) 中所有点距离的最小值,类似 \(\text{Prim}\) 算法中集合距离的定义。
则点权 \(w\) 一定满足 \(dist[S_{left}][S_{right}]\)。
由于已经对边进行了排序,因此第一个连通 \(S_{left}\) 与 \(S_{right}\) 的边一定是所有连通 \(S_{left}\) 与 \(S_{right}\) 中最小的。
通过这个思路,我们可以简单证明 \(\text{Kruskal}\) 重构树的一些性质:
- \(\text{Kruskal}\) 重构树是二叉树
即一个点最多有两个子树,显然,一条边最多能连接两个集合,得证。
- 方节点满足堆的性质。
即深度小的节点权重一定 \(\geq\) 深度大的节点权重。因为深度大的节点一定比深度小的节点先枚举到,而先枚举意味着它一定不严格大于后枚举的元素。
- \(\text{Kruskal}\) 重构树的根节点一定是最后一个处理的方节点。
由性质2可知,根节点一定是所有节点中点权最大者,最后一个处理的边一定最大,因此最后一个处理的方节点一定是根节点。
- 任意两点的 \(\text{LCA}\) 就是原图中它们最小瓶颈路中的最大边权。
继续拿这棵树举例子,假设我们要求找到 \(1\) 和 \(5\) 之间的最小瓶颈路中的最大边权,那么它们的 \(\text{LCA}\) 即为方点 \(2\)。
\(\text{LCA}\) 指最近公共祖先,那么现在就有了两个问题:
为什么这个方点一定是公共祖先?
可以把走重构树类比成一个 \(\text{Kruskal}\) 的过程,选取了一个方点意味着选取了它子树中所有的方点(边),此方点连通了它两个子树中的圆点集合,因此只有 \(1\) 和 \(5\) 的公共祖先才能使 \(1\) 和 \(5\) 连通。
为什么这个方点一定是最近的公共祖先?
因为 \(\text{Kruskal}\) 重构树第二个性质:“方节点满足堆的性质”,所以在保证连通的情况下(等价于是 \(1\) 和 \(5\) 的公共祖先),要使最大边权最小,这就要求使得方节点点权尽可能地小,深度尽可能地大,也就是最近的公共祖先——\(\text{LCA}\)。
\(\text{Kruskal}\) 重构树最重要的性质就是 “任意两点的 \(\text{LCA}\) 就是原图中它们最小瓶颈路中的最大边权”,根据它我们可以轻松解决最小瓶颈路问题。
应用
[NOIP2013 提高组] 货车运输(最大瓶颈路)
BZOJ3732 Network(最小瓶颈路)
这两题都是 \(\text{Kruskal}\) 重构树的板子题,基本是一模一样的。
此处是Network的代码,\(\text{LCA}\) 用倍增实现。
// Author: Moyou
// Copyright (c) 2022 Moyou All rights reserved.
// Date: 2022-12-30 09:24:04
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
const int N = 6e4 + 10, M = 1e5 + 10, K = 2e4 + 10;
struct E
{
int a, b, c;
} edge[M];
int n, m, T;
int fa[N], w[N], idx;
int depth[N], f[N][25];
int find(int x)
{
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
vector<int> g[N + M];
void build() // 构建Kruskal重构树
{
cin >> n >> m >> T;
for (int i = 1; i <= 2 * n; i++)
fa[i] = i;
for (int i = 1; i <= m; i++)
cin >> edge[i].a >> edge[i].b >> edge[i].c;
sort(edge + 1, edge + m + 1, [](E a, E b) { return a.c < b.c; }); // 由于是最小瓶颈路所以从小到大排序
idx = n; // 记录方节点编号
for (int i = 1; i <= m; i++)
{
int x = find(edge[i].a), y = find(edge[i].b);
if (x == y)
continue;
w[++idx] = edge[i].c; // 记录方节点点权
g[idx].push_back(x), g[idx].push_back(y); // 连方节点两棵子树
fa[x] = fa[y] = idx;
}
}
void depth_dfs(int p, int pa) // 倍增LCA,预处理深度与倍增数组
{
depth[p] = depth[pa] + 1;
f[p][0] = pa;
for (int i = 1; i <= 20; i++)
f[p][i] = f[f[p][i - 1]][i - 1];
for (auto i : g[p])
{
if (pa == i)
continue;
depth_dfs(i, p);
}
}
int lca(int a, int b) // LCA
{
if (depth[a] < depth[b])
swap(a, b);
for (int i = 19; i >= 0; i--)
if (depth[f[a][i]] >= depth[b]) // 先跳到同一高度
a = f[a][i];
if (a == b)
return a;
for (int i = 19; i >= 0; i--) // 再一起往上跳
if (f[a][i] != f[b][i])
a = f[a][i], b = f[b][i];
return f[a][0];
}
int main()
{
build();
depth[idx] = 1, depth[0] = 0;
depth_dfs(idx, 0);
while (T--)
{
int a, b;
cin >> a >> b;
cout << w[lca(a, b)] << '\n';
}
return 0;
}

 Kruskal重构树
Kruskal重构树