[CF1422D] Returning Home 题解

题目描述

一个\(n \times n\)的网格,求两点间最短用时。

你可以用一分钟向上下左右任意一个方向移动一格.特别的,城市中有\(m\)个传送点,第\(i\)个的坐标为\((x_{i},y_{i})\).当你与一个传送点横坐标相同或纵坐标相同,那么你就可以瞬间传送到该传送点.

求到达目的地的最短用时.

\(1 \leq n \leq 10^9,1 \leq m \leq 10^5,1 \leq s_{x},s_{y},f_{x},f_{y},x_{i},y_{i} \leq n\).

想法

首先看到数据范围，发现 \(n \leq 10^9\)，这就代表我们绝对不可能把所有的点存下来，但是与之相比 \(m \leq 10^5\) 就很友好了，于是从关键点 \(m\) 破题。

考虑把 \(m\) 个点在新图中建出来，那么现在我们就缺边了。

有一种朴素的想法是每两个点之间都连一条边，空间复杂度 \(O(m^2)\)，会爆掉。

如何进行优化呢？

其实原图中有些边是用不到的，比如：

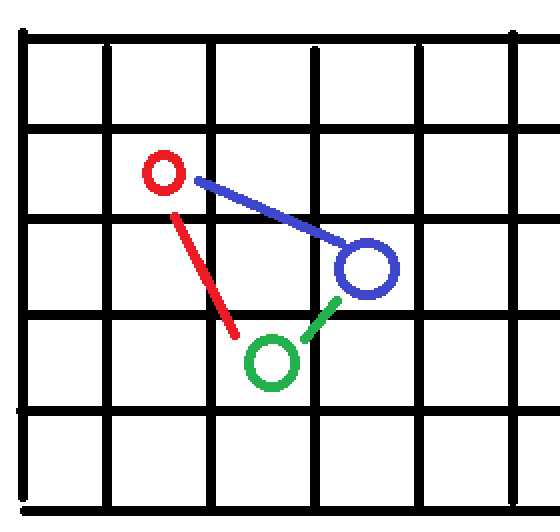
在这样一张图中，红蓝绿点两两连边，其中蓝色的边在横坐标意义上是冗余的，因为此时红点到蓝点可以选择 \(红\rightarrow 绿 \rightarrow 蓝\) 这条路径到达蓝点，而由于题目的特殊性质，这条路径其实是与原边等价的，我们只保留路径就好了。

或者更进一步地，我们说，一条边在横坐标意义上不是冗余的，当且仅当他连接的两点横坐标间没有其他点，纵坐标同理。

也许有人不理解何为横纵坐标意义下。

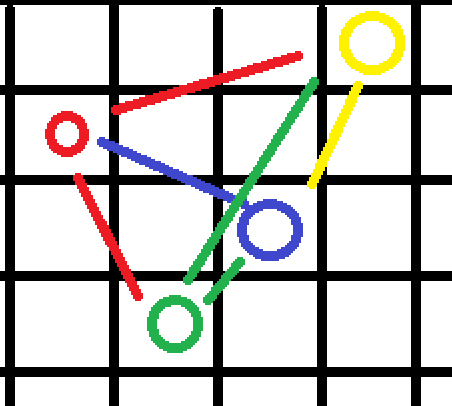
取一个极端的例子，这时这条边 \(绿\rightarrow 黄\) 无论是横坐标还是纵坐标来看都是冗余的，都可以被其他路径等效替代。

思路

由此萌发思路：只连接横坐标相邻的两点与纵坐标相邻的两点。

这时连边空间复杂度就是 \(O(m)\) 量级的。

实现

分别以点的 \(x,y\) 坐标为关键字排序，连接相邻的点即可。

实现的时候需要另外连起点到所有特殊点，与所有特殊点到终点的特殊边。

Trick： 以 \(0\) 和 \(m + 1\) 编号起点和终点。

照常 \(\text{Dijkstra}\)，时间复杂度 \(O(m\log n)\)。

// Problem: Returning Home
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF1422D
// Memory Limit: 250 MB
// Time Limit: 2000 ms
// Author: Moyou
// Copyright (c) 2022 Moyou All rights reserved.
// Date: 2022-12-20 22:18:46

#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
#include <queue>
#define x first
#define y second
#define int long long
#define INF 1e18
using namespace std;
typedef pair<int, int> PII;

const int N = 2e5 + 10, M = (N << 3);

struct node
{
    int id;
    int x, y;
} a[N];

int h[N], ne[M], e[M], w[M], idx;
void add(int a, int b, int c)
{
    e[++idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx;
}

int calc(PII a, PII b)
{
    return abs(a.x - b.x) + abs(a.y - b.y);
}

int n, m;
int dist[N];
bool st[N];
int dijkstra(int s)
{
    for (int i = 0; i <= m + 1; i++)
        dist[i] = INF, st[i] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, s});
    dist[s] = 0;
    while (heap.size())
    {
        auto t = heap.top().y;
        heap.pop();
        if (st[t])
            continue;
        st[t] = 1;
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                heap.push({dist[j], j});
            }
        }
    }
    return dist[m + 1];
}

signed main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m >> a[0].x >> a[0].y >> a[m + 1].x >> a[m + 1].y;
    a[0].id = 0, a[m + 1].id = m + 1;

    for (int i = 1; i <= m; i++)
        cin >> a[i].x >> a[i].y, a[i].id = i;

    add(0, m + 1, calc({a[0].x, a[0].y}, {a[m + 1].x, a[m + 1].y}));
    for (int i = 1; i <= m; i++)
    {
        add(0, i, min(abs(a[0].x - a[i].x), abs(a[0].y - a[i].y)));
        add(i, m + 1, abs(a[m + 1].x - a[i].x) + abs(a[m + 1].y - a[i].y));
    }

    sort(a + 1, a + m + 1, [](node a, node b) { return a.x < b.x; });
    for (int i = 1; i < m; i++)
        add(a[i].id, a[i + 1].id, a[i + 1].x - a[i].x), add(a[i + 1].id, a[i].id, a[i + 1].x - a[i].x);

    sort(a + 1, a + m + 1, [](node a, node b) { return a.y < b.y; }); // Lambda表达式，作用等同cmp函数
    for (int i = 1; i < m; i++)
        add(a[i].id, a[i + 1].id, a[i + 1].y - a[i].y), add(a[i + 1].id, a[i].id, a[i + 1].y - a[i].y);

    cout << dijkstra(0) << endl;
    return 0;
}