[ABC077D] Small Multiple 题解

[ABC077D] Small Multiple

题意：

给定一个整数 \(K\)。求一个 \(K\) 的正整数倍 \(S\)，使得 \(S\) 的数位累加和最小。

\(2 \le K \le {10}^5\)
\(K\) 是整数。

思路

只看题目完全看不出来的 同余最短路

我们约定

• \(sum[x]\) 表示 \(x\) 的数位和；

• \(f[i]\) 为 \(\min{sum[x](x\equiv i\pmod k)}\)，表示在模 \(k\) 余 \(i\) 的所有自然数中的最小数位和。

即把所有的自然数按照模 \(k\) 的结果分成 \(k\) 类 \(0, 1, 2, \dots (k - 1)\)

根据题意可以发现：

• 题目中的 \(k \geq 2\)，也就是说，对于 \(f[1]\) 而言，无论是什么数，\(1\) 一定是最小的，因为如果比 \(1\) 还小就是 \(0\) 了。

以 \(f[1] = 1\) 为跳板继续思考：

• 假如我们有一种方法可以让所有的 \(f[i]\) 从 \(f[1]\) 转移过来就可以轻松求出答案 \(f[0]\) 了。

有一个很朴素的想法：

• 对于一个数 \(x(x \equiv i\pmod k)\)，它 \(+1\) 后，一定满足 \(x'(x'\equiv i + 1\pmod k)\)，用公式写出来即为 \(sum[x] \le sum[(x + 1)\bmod k] + 1\)

• 对于一个数 \(x(x \equiv i\pmod k)\)，它 \(\times 10\) 后，即变为 \(\overline{x0}\)，一定满足 \(x'(x'\equiv i\pmod k)\)，用公式写出来即为 \(sum[x] \le sum[(10x)\bmod k]\)。

由于在模 \(k\) 意义下，\(f[i] = sum[x](x\equiv i\pmod k)\)，因此将上述公式整理后，得：

\[\left\{ \begin{aligned} f[i] &\le f[i + 1] + 1\\ f[i] &\le f[10\times i] \end{aligned} \right. \]

这不就是差分约束吗！

因此我们将所有的模数可能性视作一个点，将 \(i\) 到 \(i + 1\) 连一条长度为 \(1\) 的边，\(i\) 到 \(10i\) 连一条长度为 \(0\) 的边，这种情况我们不用跑 \(\text{SPFA}\)了，因为从 \(1\) 开始必定能遍历到所有点，并且权值只有 \(0, 1\)，直接跑一遍 \(\text{双端队列BFS}\) 即可，最后 \(f[0]\) 即为答案。

模拟

在模 \(7\) 意义下，建出来的图如下：

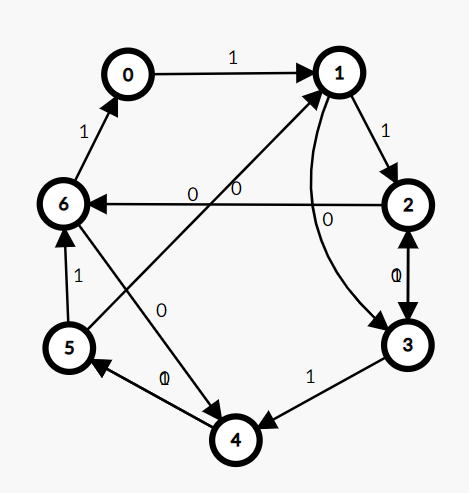
走法：1-3-2-6-0

Show the Code

// Problem: [ABC077D] Small Multiple
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/AT_arc084_b
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// Author: Moyou
// Copyright (c) 2022 Moyou All rights reserved.
// Date: 2022-11-27 19:53:48

#include <cstring>
#include <iostream>
#include <queue>
using namespace std;

const int N = 1e5 + 10, M = 2e5 + 10;

int h[N], ne[M], e[M], w[M], idx;
int k;
int dist[N];
bool st[N];
void add(int a, int b, int c)
{
    e[++idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx;
}

void bfs(int s)
{
    memset(dist, 0x3f, sizeof dist);
    dist[s] = 1;
    deque<int> q;
    q.push_front(s);
    while (q.size())
    {
        auto t = q.front();
        q.pop_front();
        if (st[t])
            continue;
        st[t] = 1;
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if (w[i] == 0)
                    q.push_front(j);
                else
                    q.push_back(j);
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> k;
    for (int i = 1; i <= k; i++)
    {
        add(i, (i + 1 > k ? 1 : i + 1), 1);
        add(i, (i * 10 % k), 0);
    }
    bfs(1);
    cout << dist[0] << endl;
    return 0;
}