树上倍增LCA 算法笔记
树上倍增LCA
定义
LCA（Least Common Ancestors），即最近公共祖先，是指在有根树中，找出某两个节点u和v最近的公共祖先。
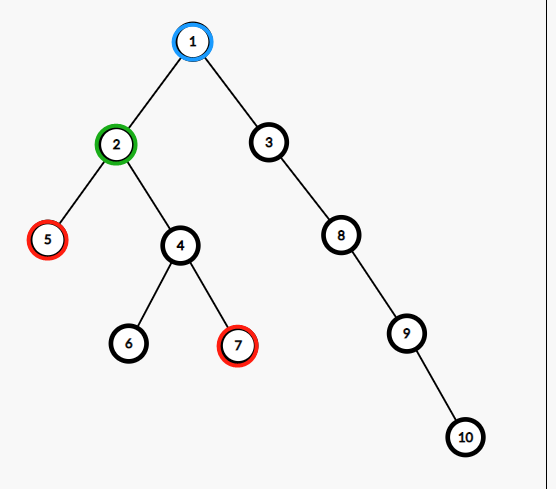
假设有这么一棵树。
其中 \(5\) 的祖先有 \(2, 1\)，\(7\) 的祖先有 \(4, 2, 1\)，因此，他们的公共祖先有 \(2\) 和 \(1\) 显然 \(2\) 相比 \(1\) 距离两个点更近，因此我们称 \(2\) 是 \(5\) 和 \(7\) 的最近公共祖先，记作 \(\texttt{lca}(5, 7) = 2\)
想法
很多时候算法来源于人类的思维，我们把自己带入计算机中，假如你是计算机，你会怎么解决这个问题。
相信大多数人第一个想到的就是先找到两个点的公共祖先，再找最近的。
那么一个朴素的想法就诞生了，先从一个点开始，给所有祖宗节点打上标记，再从另一个点开始，第一个碰到的打上标记的节点就是他们的 \(\texttt{LCA}\)。
倍增思想
但是对于这一道题，我们使用上述方法只能拿 \(70\) 分，于是我们考虑对上述做法进行优化。
首先想一下这个算法最浪费时间的地方在哪里，很明显，是一个个打上标记，一个个找祖先的过程。
太谨慎了！
其实我们可以采用一种 “大跨步找祖先” 的思想，倍增思想。
倍增的关键在于，一个数一定可以拆分成 \(2^a + 2^b + .. + 2^k\) 次方的形式，证明很简单，任何一个数都可以用二进制表示，比如 \(11 = (1011)_2 = 2^3 + 2^1 + 2^0\)，而二进制也可以通过 \(2^k\) 之和的形式来表示，得证。
所以如果我们要跨 \(x\) 步到达某个节点，那么就可以拆分为 \(x = 2^a + 2^b + ... + 2^k\) 于是只要我们能预处理出 \(2^i\)，我们就能成功地把一个 \(O(n)\) 的算法转化成一个 \(O(\log n)\) 的算法！
思路
将这个思想运用到这道题中，即是预处理出所有从 \(i\) 开始跳 \(2^{j}\) 可达的所有节点即可，记 \(fa[i][j]\) 为 \(从i开始跳2^j能到达的节点编号\)，\(depth[i]\) 为 \(i的深度（层数）\)
树上倍增LCA分为两个步骤
- 将查询的两个点 \(a, b\) 对齐在同一深度内
- \(a\) 和 \(b\)一起往上跳，跳到 \(\texttt{lca}(a, b)\) 的下一层
步骤1
“将两个点对齐” 可以使用上文提到过的二进制拼凑，用二进制拼凑让 \(a\) 从 \(depth[a]\) 跳到 \(depth[b]\)。
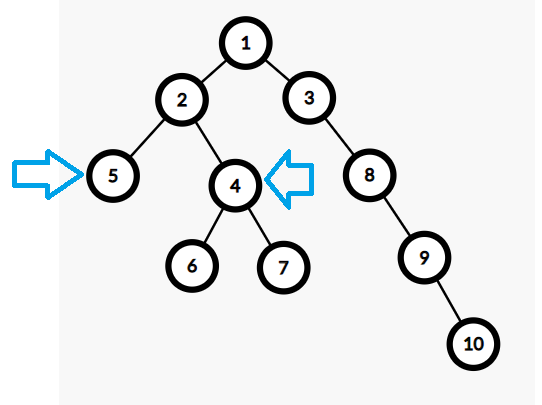
for(int i = 19; i >= 0; i --) // 枚举2的i次方
if(depth[fa[a][i]] >= depth[b]) // 如果将要跳到的点深度（层数）还是比 b 点大
a = fa[a][i]; // 就继续往上跳
步骤2
让两个点一起跳 \(2^k(1\leq k \leq \log(n))\) 步。
这里分两种情况
- 对齐后 \(a = b\)，这个时候 \(b\) 就是 \(\texttt{lca}(a, b)\)
- 对齐后 \(a \neq b\)，开跳！
这里同样用二进制拼凑，拼凑出 \(a, b\) 到 \(\texttt{lca}(a,b)的下一层\) 的步数，最后返回 \(a\) 的上一层，即为 \(fa[a][0] = \texttt{lca(a, b)}\)。
if(a == b) return a;
for(int i = 19; i >= 0; i --)
if(fa[a][i] != fa[b][i]) // 一直往上跳直到
a = fa[a][i],
b = fa[b][i];
假设 \(a\) 和 \(b\) 分别是 \(10\) 和 \(12\)
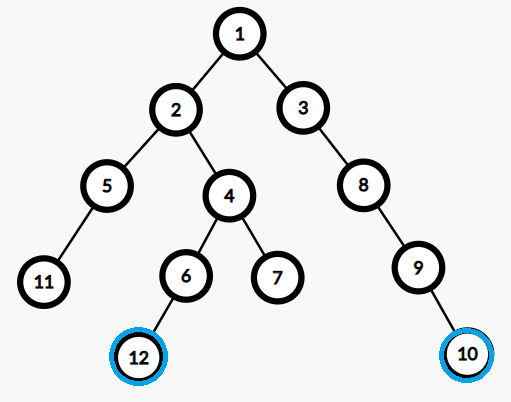
在 i == 1 之前的所有操作都步子迈大了，容易扯着蛋我们从 i == 1 开始看，这时候 \(10, 12\) 都往上跳了 \(2^i = 2^1 = 2\) 步。
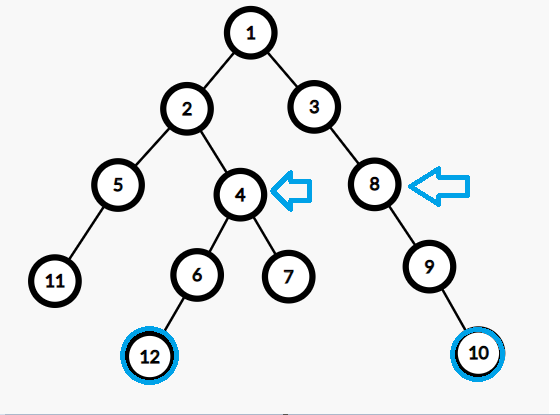
接着试一下 i == 0 发现 \(2^i = 2^0 = 1\) 步不会迈太大，因此走下去。
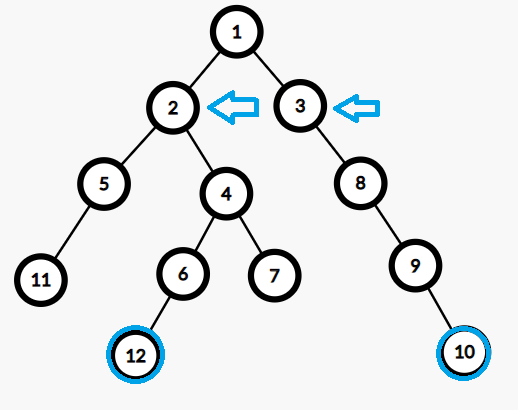
顺利结束，\(\texttt{lca}(a, b) = fa[a][0] = 1\)。
Q: 为什么跳到最近公共祖先的下一层而不直接一步到位呢？
A: 相比直接一步到位，先跳到 \(\texttt{lca}(a,b)\) 的下一层更加方便，我们不太好找到那个临界点 —— 往上一步就不够近，往下一步就不是公共祖先
Q: 如果步子迈大了如何处理？
A: 令 \(depth[0] = 0\) 如果步子迈大了 \(fa[i][j] == 0\) 就会碰到这个 “边防哨兵” 然后直接被逮捕，此时 \(depth[a][i] == depth[b][i] == 0\) 因此不会齐跳。
预处理
类似状态转移
\(fa[i][j] = fa[fa[i][j - 1]][j - 1] = (i + 2^{j - 1}) + 2^{j - 1} = i + 2^j\)
\(depth[i] = depth[father_i] + 1(father_i为i的父节点)\)
转移过程可以用 bfs 实现，以防爆栈。
void bfs(int root)
{
queue<int> q;
memset(depth, 0x3f, sizeof depth);
depth[root] = 1, depth[0] = 0;
q.push(root);
while(q.size())
{
int t = q.front(); q.pop();
for(int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if(depth[j] > depth[t] + 1)
{
depth[j] = depth[t] + 1;
q.push(j);
fa[j][0] = t;
for(int i = 1; i <= 19; i ++)
fa[j][i] = fa[fa[j][i - 1]][i - 1];
}
}
}
}
完整代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 5e5 + 10, M = N << 1;
int n, m;
int h[N], e[M], ne[M], idx;
int depth[N], fa[N][20];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void bfs(int root)
{
queue<int> q;
memset(depth, 0x3f, sizeof depth);
depth[root] = 1, depth[0] = 0;
q.push(root);
while(q.size())
{
int t = q.front(); q.pop();
for(int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if(depth[j] > depth[t] + 1)
{
depth[j] = depth[t] + 1;
q.push(j);
fa[j][0] = t;
for(int i = 1; i <= 19; i ++)
fa[j][i] = fa[fa[j][i - 1]][i - 1];
}
}
}
}
int lca(int a, int b)
{
if(depth[a] < depth[b]) return lca(b, a);
for(int i = 19; i >= 0; i --)
if(depth[fa[a][i]] >= depth[b])
a = fa[a][i];
if(a == b) return a;
for(int i = 19; i >= 0; i --)
if(fa[a][i] != fa[b][i])
a = fa[a][i],
b = fa[b][i];
return fa[a][0];
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
memset(h, -1, sizeof h);
int root;
cin >> n >> m >> root;
for(int i = 1; i <= n - 1; i ++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
bfs(root);
while(m --)
{
int x, y;
cin >> x >> y;
cout << lca(x, y) << endl;
}
return 0;
}
