查找算法浅析

本人整理的解决 "在一组数据中查找某个特定的值" 这类问题的算法

二分

二分是通过一个 mid 中点将整个函数分为两个部分，每次操作缩小\(\frac12\)的查找范围，适用于单调函数（一次函数）中的数据查找。

例如，查找一个单调递增数组中元素\(x\)的下标

int l = 1, r = n;
while(l < r)
{
    int mid = (l + r) / 2;
    if(a[mid] >= x) r = mid;
    else l = mid + 1;
}
ans = l;

三分

三分和我们熟知的二分非常像。

• 二分是通过一个 mid 中点将整个函数分为两个部分，每次操作缩小\(\frac12\)的查找范围，适用于一次函数中的数据查找。

• 三分是通过两个 mid1, mid2 将整个函数分为三个部分，每次操作缩小\(\frac23\)的范围，不仅适用于一次函数中的查找，还可以用来对数据分布为单峰函数（形如二次函数）的数据进行查找极值。

可以用三种方法实现

1. 找三等分点，三分

while(r - l > eps)
{
    double m1 = l + (r - l) / 3;
    double m2 = r - (r - l) / 3;
    if(f(m1) > f(m2)) r = m2;
    else l = m1;
}

2. 找中点，然后找靠r四等分点，三分

while(r - l > eps)
{
    double m1 = (l + r) / 2;
    double m2 = (r + m1) / 2;
    if(f(m1) > f(m2)) r = m2;
    else l = m1;
}

3. 找中点，然后分别找中点左右两边距离中点极小的两个点，三分

while(r - l > eps)
{
    double m2 = (l + r) / 2;
    if(f(m2 - eps) > f(m2 + eps)) r = m2;
    else l = m2;
}

模拟退火算法

模拟退火（Simulate Anneal）模拟的是金属工艺中的退火技术，是一个随机化算法，相比三分，它更玄学随机，并且可以处理多峰函数。

定义以下几个参数

• 当前温度（步长）\(T（\eta）\)
• 初始温度 \(T_0\)，一般是一个很大的数，如1e5
• 终止温度 \(T_E\)，一般是很接近0的一个正数，如1e-5
• 当前最优解 \(now\)
• 衰减系数 \(\Delta\)，一般是在0、1之间的一个小数，如0.999

此时假设我们要找出一个多峰函数中的最小点。

算法流程：

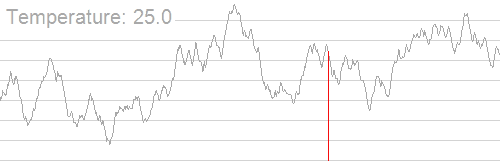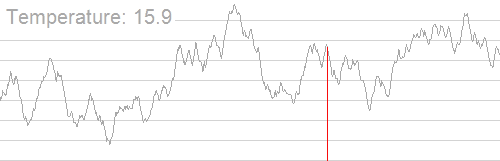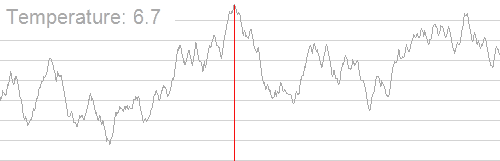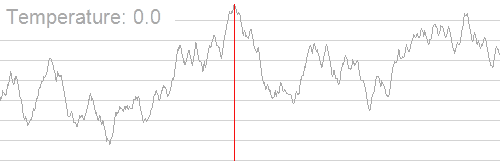
可以看到温度越低，解来回切换的范围就越小

1. 在当前点（初始点）\(now\)周围步长区域中随机选择一个点，设其为点\(new\)，令\(f(new) - f(now) = \Delta E\)，此时温度 \(T\) 越大，随机的范围越广，解越不稳定。

此时分两种情况处理

• \(\Delta E < 0\)，即比当前最优解更优，那么我们一定接受这个解，直接将 \(now\) 设为 \(new\)；

• \(\Delta E > 0\)，即不是最优解，此时我们一定概率接受这个解，否则可能会陷入一个小局部最优的山谷而错过整体最优的大峡谷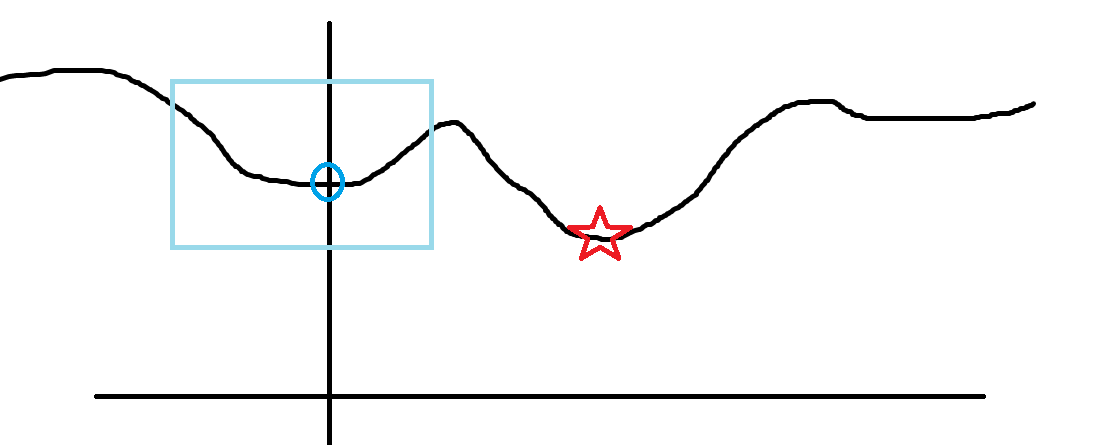如图，当当前解在蓝圈处时，我们会一直在淡蓝色区域内找，而不会考虑红星处的最优解，一般概率是 \(e^{-\frac{\Delta E}{T}}\) ，即当两者差值 \(\Delta E\) 越大，接受的概率越小，因为其越不可能是最优解。

对以上步骤进行迭代，每次迭代结束后将 \(T = T \times \Delta\)，直到 \(T\leq T_E\)。

小技巧

• 衰减系数 \(Delta\) 越大，算法越慢，同时找到最优解的可能性越大。

• 时间充裕的情况下，可以适当增加进行模拟退火的次数，由于是随机化算法，所以迭代的次数越多，找到全局最优解的概率就越大。

• 有时可以调整随机参数 \(srand()\) 以获得更多的分数（当然要是IOI或者是ACM赛制才行）。

• 如果不确定该退火多少次，可以计算时间，如果不到时间限制就一直退火，如下，当然这个方法时间上很吃亏。

#include <ctime>
...
clock_t StartTime = clock(); // 主函数开头
...
while((double)(clock() - StartTime) / CLOCKS_PER_SEC < 0.8) // 计算运行时间，这个代码的单位是秒
    sa(); 

例题

A Star not a Tree?

简化题意

在二维平面上有 \(n\) 个点，第 \(i\) 个点的坐标为 \((x_i,y_i)\)。

请你找出一个点，使得该点到这 \(n\) 个点的距离之和最小。

思路

几乎是模拟退火的模板题，\(f(x,y)\) 函数值即为 \((x,y)\) 到每个点的距离和，当然此处是欧几里得距离。

函数计算：

double f(PDD x)
{
    double res = 0; // 距离和
    for(int i = 1; i <= n; i ++)
    {
        res += sqrt(pow(1.0 * p[i].x - x.x, 2) + pow(1.0 * p[i].y - x.y, 2)); // 两点之间坐标公式，勾股定理
    }
    ans = min(ans, res); // 更新答案
    return res;
}

模拟退火函数：

void sa() // Simulate Anneal
{
    PDD now = {rd(0, 10000), rd(0, 10000)}; // 先随机一个点作为初始点
    for(double t = 1e4; t >= 1e-4; t *= delta) // 由于数据范围最多就是1e4所以初始温度和终止温度都干脆取1e4和1e-4
    {
        PDD newp = {rd(now.x - t, now.x + t), rd(now.y - t, now.y + t)}; // 在步长（温度）内随机选择一个数，作为新点
        double deltat = f(newp) - f(now); // 计算函数差值，注意不要写反了
        if(deltat < 0) // 更优的解？
            now = newp; // 直接环
        else if(exp(-deltat / t) > rd(0, 1)) // 即上文的随机概率
            now = newp; // 概率换
    }
}

完整代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <ctime>
#include <cmath>
#define x first
#define y second
using namespace std;

typedef pair<double, double> PDD; // 点的坐标
const int N = 110;
const double delta = 0.9; // 衰减系数

PDD p[N];
int n;
double ans = 1e9; // 最优解
double T = 0; // 当前温度

double rd(double l, double r) // 在l~r之间的一个浮点随机数
{
    return 1.0 * rand() / RAND_MAX * (r - l) + l;
}

double f(PDD x)
{
    double res = 0;
    for(int i = 1; i <= n; i ++)
    {
        res += sqrt(pow(1.0 * p[i].x - x.x, 2) + pow(1.0 * p[i].y - x.y, 2));
    }
    ans = min(ans, res);
    return res;
}

void sa() // 模拟退火
{
    PDD now = {rd(0, 10000), rd(0, 10000)};
    for(double t = 1e4; t >= 1e-4; t *= delta)
    {
        PDD newp = {rd(now.x - t, now.x + t), rd(now.y - t, now.y + t)};
        double deltat = f(newp) - f(now);
        if(deltat < 0)
            now = newp;
        else if(exp(-deltat / t) > rd(0, 1))
            now = newp;
    }
}

int main()
{
    srand(114514); // 神秘数字
    clock_t StartTime = clock(); // 计时
    ios::sync_with_stdio(0); cin.tie(0), cout.tie(0); // 解除cin cout同步流
    cin >> n;
    for (int i = 1; i <= n; i ++ )
        cin >> p[i].x >> p[i].y;
    while((double)(clock() - StartTime) / CLOCKS_PER_SEC < 0.8) sa();
    printf("%.0lf\n", ans);
    return 0;
}