BFS基本操作及其技巧

阅读本博客前建议先学习BFS

Flood Fill 泛洪算法

Lake Counting

顾名思义，此算法就如同洪水泛滥一样遍历每个情况，从源点开始向四周扩展，主要处理连通块问题

Code

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 120;
typedef long long LL;

struct node
{
    int x, y;
};

int n, m ,cnt = 0; // cnt记录水坑数量
char ch[N][N];
int dx[8] = {-1, 0, 1, 1, 1, 0, -1, -1}, dy[8] = {1, 1, 1, 0, -1, -1, -1, 0}; // 方向盘，方便记录下一个坐标

void bfs(int x, int y)
{
    queue<node> q;
    node srt;
    srt.x = x;
    srt.y = y;
    q.push(srt); // 推进起始位置

    while(q.size())
    {
        node a = q.front();
        
        q.pop();
        for(int i = 0; i < 8; i++) // 八连通
        {
            node t;
            t.x = a.x + dx[i];
            t.y = a.y + dy[i];

            if(t.x >= 0 && t.x < n && t.y >= 0 && t.y < m && ch[t.x][t.y] == 'W') // 如果合法
            {
                ch[t.x][t.y] = '.'; // 走过了的点和干地性质，也可用vis / st数组记录走过的点，以防重复查找
                q.push(t); // 推入bfs，继续找
            }
        }
    }
}

int main()
{
    cin >> n >> m;

    for(int i = 0; i < n; i++) cin >> ch[i];

    for(int i = 0; i < n; i++)
        for(int j = 0; j < m; j++)
        {
            if(ch[i][j] == 'W') // 如果是水坑
            {
                bfs(i, j);
                cnt++; // 水坑的数量++
            }
        }
    cout << cnt << endl;
    return 0;
}

山峰和山谷

一本通在线评测

题目描述

给定一个 \(n×n\) 的网格状地图，每个方格 \((i,j)\)有一个高度 \(w_{i_j}\) 。如果两个方格有公共顶点，则它们是相邻的。

定义山峰和山谷如下：

均由地图上的一个连通块组成；

所有方格高度都相同；

周围的方格（即不属于山峰或山谷但与山峰或山谷相邻的格子）高度均大于山谷的高度，或小于山峰的高度。

求地图内山峰和山谷的数量。特别地，如果整个地图方格的高度均相同，则整个地图既是一个山谷，也是一个山峰。

输入

第一行一个整数\(n （2≤n≤1000）\)，表示地图的大小。

接下来 \(n\) 行每行 \(n\) 个整数表示地图。第 \(i\) 行有 \(n\) 个整数 \(w_{i_1}, w_{i_2}, \ldots, w_{i_n} (0 \le w_{i_j} \le 1\ 000\ 000\ 000)\)，表示地图第 \(i\) 行格子的高度。

输出

输出一行两个整数，分别表示山峰和山谷的数量。

样例

5
8 8 8 7 7
7 7 8 8 7
7 7 7 7 7
7 8 8 7 8
7 8 8 8 8

2 1

提示

样例1解释：

样例输入2:

5
5 7 8 3 1
5 5 7 6 6
6 6 6 2 8
5 7 2 5 8
7 1 0 1 7

样例输出2:

3 3

样例2解释：

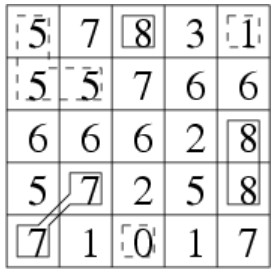
在FloodFill的基础上加上对山峰和山谷的判断

Code

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#define INF 0x3f3f3f3f

using namespace std;

const int N = 1010;
typedef long long LL;

int m[N][N];
bool vis[N][N];
bool v, h;
int dx[9] = {0, 1, 1, 1, 0, -1, -1, -1}, dy[9] = {1, 1, 0, -1, -1, -1, 0, 1}; // 方向盘
int hill, valley; // 记录山峰，山谷的数量
int n;
struct node
{
    int x, y;
};

void bfs(int i, int j)
{
    queue<node> q;
    q.push({i, j});
    vis[i][j] = true;
    while(q.size())
    {
        node t = q.front();
        q.pop();
        for(int i = 0; i < 8; i ++)
        {
            int x = t.x + dx[i], y = t.y + dy[i];
            if(x < 1 || x > n || y < 1 || y > n) continue;
            if(m[x][y] != m[t.x][t.y])
            {
                if(m[x][y] < m[t.x][t.y]) v = false; // 不符合山谷的定义
                else h = false; // 同上
            }
            else if(!vis[x][y])  // 如果是一个联通块的
            {
                q.push({x, y}); // 更新bfs
                vis[x][y] = true;
            }
        }
    }
}

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i ++) 
        for(int j = 1; j <= n; j ++)
            cin >> m[i][j];
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= n; j++)
            if(!vis[i][j])
            {
                h = v = true; // h == 1 => 是山峰 v == 1 => 是山谷
                bfs(i, j);
                if(h) hill ++;
                else if(v) valley++;
            }
                
    cout << hill << " " << valley << endl;
    return 0;
}

最短路模型

迷宫问题

一本通在线评测

定义一个二维数组：

int maze[5][5] = {
0,1,0,0,0,
0,1,0,1,0,
0,0,0,0,0,
0,1,1,1,0,
0,0,0,1,0,
};

它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。

输入

一个5 × 5的二维数组，表示一个迷宫。数据保证有唯一解。

输出

左上角到右下角的最短路径，格式如样例所示。

输入样例：

0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出样例：

(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)

这题很大部分难度在于对于上一步的记录，本博客使用递归处理，$$step[i][j]记录走到(i, j)的点的方位$$，其余bfs板

Code

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#define INF 0x3f3f3f3f
using namespace std;
const int N = 5; // 方便调试
typedef long long LL;

int maze[N][N]; // 地图
int dx[5] = {0, 1, 0, -1}, dy[5] = {1, 0, -1, 0}; // 方向盘
struct node
{
    int x, y;
}step[N][N]; // 记录上一步

void print(int x, int y)
{
    if(x == 1 && y == 1) // 递归边界条件：找到起点
    {
        printf("(%d, %d)\n", 0, 0); // 输出起点下标0, 0
        return;
    }
    print(step[x][y].x, step[x][y].y); // 递归寻找上一步
    printf("(%d, %d)\n", x - 1, y - 1); // 由于下标从1开始，题目中要求输出从0开始，所以要-1
}

void bfs(int x, int y)
{
    queue<node> q; // bfs板
    node srt;
    srt.x = x;
    srt.y = y;
    q.push(srt);

    while(q.size())
    {
        node a = q.front();
        q.pop();
        for(int i = 0; i < 4; i++)
        {
            int xx = a.x + dx[i], yy = a.y + dy[i];
            if(xx > 0 && xx <= N && yy > 0 && yy <= N && maze[xx][yy] == 0)
            {
                maze[xx][yy] = 1;
                q.push({xx, yy});
                step[xx][yy] = a; // 记录如何到(xx, yy)的
            }
        }
    }
}
int main()
{
    for(int i = 1; i <= N; i ++)
        for(int j = 1; j <= N; j ++)
            cin >> maze[i][j];
    bfs(1, 1);
    print(5, 5); // 从终点开始往前找
    return 0;
}

抓住那头牛

农夫知道一头牛的位置，想要抓住它。农夫和牛都位于数轴上，农夫起始位于点\(N(0≤N≤100000)\)，牛位于点\(K(0≤K≤100000)\)。农夫有两种移动方式：

1、从\(X\)移动到\(X-1\)或\(X+1\)，每次移动花费一分钟

2、从\(X\)移动到\(2*X\)，每次移动花费一分钟

假设牛没有意识到农夫的行动，站在原地不动。农夫最少要花多少时间才能抓住牛？

输入

两个整数，\(N\)和\(K\)。

输出

一个整数，农夫抓到牛所要花费的最小分钟数。

样例

5 17

4

来源

一本通在线评测

\[step[i]记录到第i个点需要的步数 \]

\[vis[i]记录第i个点是否被走过 \]

Code

#include <iostream>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 10;

int n, k;
int vis[N], step[N];

void bfs()
{
    queue<int> q;
    q.push(n);
    vis[n] = true; // mark
    step[n] = 0; // 起点到自己走0步
    while(q.size())
    {
        int t = q.front();
        q.pop();
        if(t == k) // 即找到了
        {
            cout << step[k] << endl; // 直接输出
            return; // 结束bfs
        }
        int d[3] = {t + 1, t - 1, t * 2}; // 方向盘
        for(int i = 0; i < 3; i ++)
        {
            int x = d[i];
            if(x >= 0 && x < N && !vis[x]) // 合法且未走过
            {
                q.push(x); // 继续bfs
                vis[x] = true; // mark
                step[x] = step[t] + 1; // 增加步数
            }
        }
    }
}
int main()
{
    cin >> n >> k;
    bfs();

    return 0;
}

多源BFS

即将多个起始源点放入BFS队列中

矩阵距离

题目意思

对于每一个点，输出\(a[i][j]\)到最近的"1"的距离

解法

多源bfs即源点有多个

我们在做普通bfs的时候，通常只需要在一开始给队列里推进一个源点，但是这道题需要推进多个源点，这就是二者的不同

\[dist[i][j]表示题目中的b[i][j]，记录a[i][j]到它最近的"1"的距离 \]

Code

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#define x first
#define y second
#define INF 0x3f3f3f3f

using namespace std;

const int N = 1010;
typedef long long LL;
typedef pair<int, int> PII;

bool a[N][N];
int dist[N][N];
int n, m;
int dx[4] = {0, 1, 0, -1}, dy[4] = {1, 0, -1, 0};

void bfs()
{
    memset(dist, -1, sizeof dist); // 初始化，-1表示未走过
    queue<PII> q;
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < m; j ++) // 循环找到源点"们"
            if(a[i][j])
            {
                q.push({i, j});
                dist[i][j] = 0; // 推进源点，距离设为0
            }

    while(q.size())
    {
        PII t = q.front();
        q.pop();
        for(int i = 0; i < 4; i ++)
        {
            int x = t.x + dx[i], y = t.y + dy[i];
            if(x < 0 || x >= n || y < 0 || y >= m) continue; // 不合法就跳过
            if(dist[x][y] == -1) // 未走过则推入队列
            {
                dist[x][y] = dist[t.x][t.y] + 1; // 路径长度++
                q.push({x, y});
            }
        }

    }
}

int main()
{
    cin >> n >> m;
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < m; j ++)
        {
            char ch;
            cin >> ch;
            a[i][j] = ch - '0'; // 由于cin会把一行当做一个int读入，所以需要char先存一下，血的教训>_<
        }
            
        
    bfs();
    for(int i = 0; i < n; i ++)
    {
        for(int j = 0; j < m; j ++)
            cout << dist[i][j] << " "; // 输出
        puts("");
    }
        

    return 0;
}

最小步数模型

魔板 Magic Squares

将魔板看成一维，寻找ABC操作的规律，之后用哈希表存储答案，排重

Code

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
#define INF 0x3f3f3f3f

using namespace std;
typedef long long LL;

string st = "12345678", tg;
unordered_map<string, string> h;

string change(int op, string a)
{
    if(op == 1)
    {
        reverse(a.begin(), a.end());
    }
    else if(op == 2)
    {
        for(int i = 3; i > 0; i --)
        {
            swap(a[i], a[i - 1]);
            swap(a[7 - i], a[8 - i]);
        }
    }
    else 
    {
        swap(a[1], a[2]);
        swap(a[1], a[5]);
        swap(a[1], a[6]);
    }
    return a;
}

void bfs()
{
    queue<string> q;
    q.push(st);
    h[st] = "";
    while(q.size())
    {
        auto t = q.front();
        q.pop();
        string d[3] = {change(1, t), change(2, t), change(3, t)};
        for(int i = 0; i < 3; i ++)
        {
            string x = d[i];
            if(!h.count(x))
            {
                h[x] += h[t] + char(i + 'A');
                if(x == tg) return;
                q.push(x);
            }
        }
    }
}


int main()
{
    int n = 8;
    for(int i = 0; i < n; i++)
    {
        int t;
        cin >> t;
        tg += char(t + '0');
    }
    
    if(tg == st)
    {
        cout << h[tg].size() << endl << h[tg] << endl;
        return 0;
    }
    
    bfs();

    cout << h[tg].size() << endl << h[tg] << endl;
    return 0;
}

双端队列BFS

题目

给定一个图，图的边权为\(0\sim 1\)，求边权和最小的路径长度

铺好的电线就是0，没铺好的是1

算法分析

双端队列bfs相比朴素bfs只能处理权重相同的图的最短路径，它可以处理权重为\(0或1\)的图的最短路径

细节： 采用一个\(deque代替queue\)存储处理要处理的点，其中：

1. 要拓展的点的边权为1，则推入队尾

2. 要拓展的点的边权为0，则推入队头

原因：贪心处理边权为 \(0\) 的边，可以发现 deque 可以看成狭义上的堆，是阉割版的 \(\text{Dijkstra}\)。

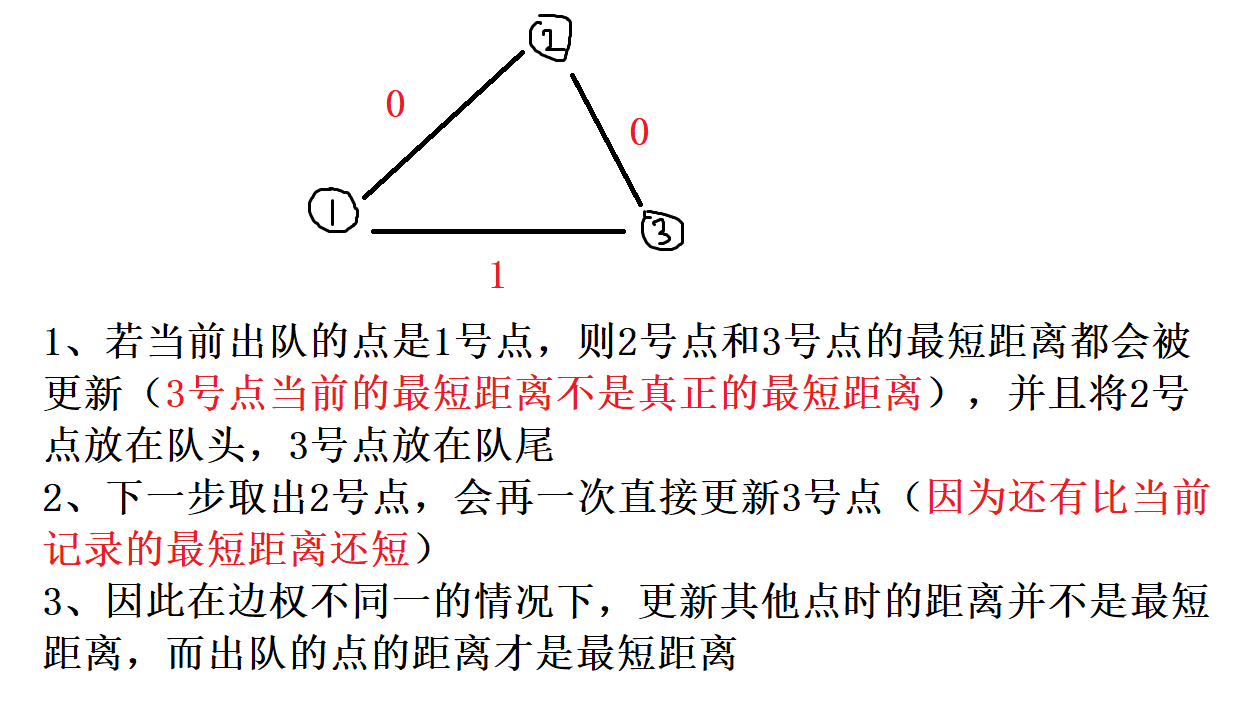
此题特色

此题特色在于对于方向盘(dx, dy, ix, iy)的处理

如下图：

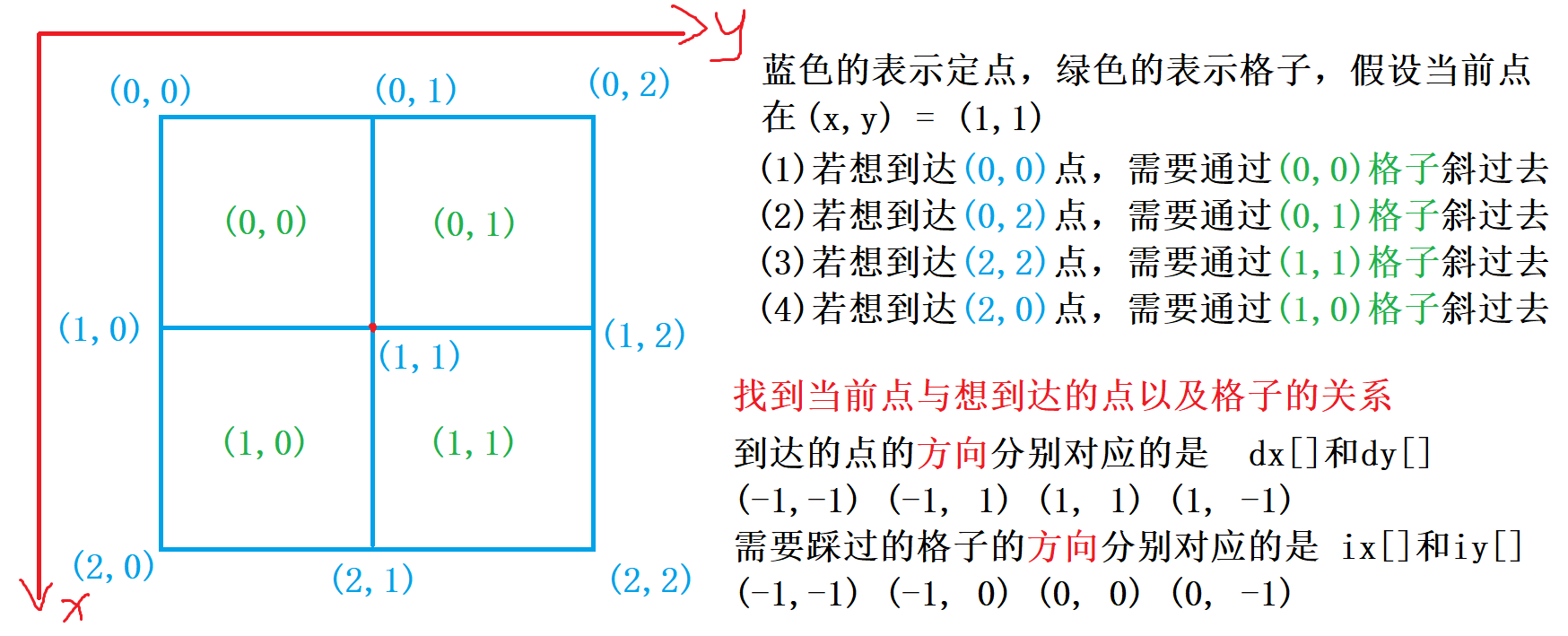
方向盘：

1. 用\(dx[], dy[]\)表示更新其他点方位的方向盘

2. 用\(ix[], iy[]\)表示更新某个点需要经过的边的方向盘

Code

#include <iostream>
#include <cstring>
#include <algorithm>
#include <deque>
#define INF 0x3f3f3f3f
#define N 510
using namespace std;
struct PII
{
    int x, y;
};

char g[N][N];
char str[] = "\\/\\/"; // '\'是转义符，所以要多加一个
int d[N][N];
int ix[4] = {-1, -1, 0, 0}, iy[4] = {-1, 0, 0, -1}; // 方向盘
int dx[4] = {-1, -1, 1, 1}, dy[4] = {-1, 1, 1, -1};
bool st[N][N];

int bfs(int n, int m)
{
    memset(d, 0x3f, sizeof d); // distance初始化
    deque<PII> q;
    q.push_front({0, 0}); // 推进起点
    d[0][0] = 0; // 起点到自身的距离为0

    while(q.size())
    {
        auto t = q.front();
        q.pop_front();

        int x = t.x, y = t.y;

        if(st[x][y]) continue; // 走过了就跳过
        st[x][y] = true;  // 标记

        for(int i = 0; i < 4; i ++)
        {
            int px = x + dx[i], py = y + dy[i]; // 点坐标
            if(px < 0 || px > n || py < 0 || py > m) continue; // 去掉不合法的情况

            int ca = x + ix[i], cb = y + iy[i]; // 边坐标

            int t = d[x][y] + (g[ca][cb] != str[i]); // 原距离加上代价

            if(d[px][py] > t) // 相当于Dijkstra用t更新距离
            {
                d[px][py] = t; // 最短路径更新

                if(g[ca][cb] == str[i]) q.push_front({px, py}); // 权值为0，推入队头
                else q.push_back({px, py}); // 权值为1，推入队尾
            } 
        }
    }
    return d[n][m];
}

int main()
{
    int T = 1; // 由于SWOJ的题只有一套数据
    while(T --)
    {
        int n, m;
        cin >> n >> m;
        for(int i = 0; i < n; i ++)
                scanf("%s", g[i]);

        int t = bfs(n, m);

        if (t == 0x3f3f3f3f) puts("NO SOLUTION"); // 也可以直接找出规律，但是我不会@_@
        else printf("%d\n", t);
    }

    return 0;
}

双向BFS

子串变换

此题数据限制严格，因此采取双向bfs，从起始状态和中止状态分别开始bfs，时间复杂度\(O((LN)^5)\)

Code

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>
#define INF 0x3f3f3f3f
#define N 10
using namespace std;

string a[N], b[N];
int n;

// 扩展队列函数
int extend(queue<string>& q, unordered_map<string, int>& da, unordered_map<string, int>& db, string a[N], string b[N])
// 分别是：要扩展的队列，起点，终点，可变换字符串的规则，变换后字符串的规则
{
    
    auto t = q.front();
    q.pop();

    for(int i = 0; i < n; i ++) // 枚举规则
        for(int j = 0; j < t.size(); j ++) // 枚举扩展起点
            if(t.substr(j, a[i].size()) == a[i]) // 如果有符合规则的部分
            {
                string r = t.substr(0, j) + b[i] + t.substr(j + a[i].size()); // 把原字符串中符合规则a[]的部分替换成b[]
                if(db.count(r)) return da[t] + 1 + db[r]; // 被另一个bfs走过了，则两边bfs会师，输出最小步数
                if(da.count(r)) continue; // 被自己走过了，排除重复状态
                da[r] = da[t] + 1; // 记录步数
                q.push(r);
            }
    return 11;
}

int bfs(string A, string B)
{
    if(A == B) return 0; // 相等则无需变换
    queue<string> qa, qb;
    unordered_map<string, int> da, db;

    qa.push(A);
    qb.push(B);
    da[A] = db[B] = 0;

    int step = 0;
    while(qa.size() && qb.size())
    {
        int t;
        if(qa.size() <= qb.size()) // 优先处理数据较少的队列
            t = extend(qa, da, db, a, b); // 处理队列1
        else 
            t = extend(qb, db, da, b, a); // 处理队列2
        
        if(t <= 10) return t; // 即10步以内找到了答案
    }

    return 11; // NOT FOUND
}

int main()
{
    string st, ed;
    cin >> st >> ed;

    while(cin >> a[n] >> b[n]) n++;

    int t = bfs(st, ed);
    if(t > 10) puts("NO ANSWER!");
    else cout << t << endl;
    
    return 0;
}