高斯消元解线性方程组

初等行变换

矩阵的初等行变换是实现高斯消元的方法
初等行变换有三种

1. 某一行所有数乘$k(k\ne 0)$

2. 交换某两行
3. 将某一行加上另一行的若干倍

高斯消元

高斯消元有四种操作

1. 找到绝对值最大的一行（为了代码的稳定性）

2. 将该行移到最上面
3. 将该行第一个数变为1
4. 将最上面一行下面所有行的第$c$列变成0

以上四种操作均可通过初等行变换实现

判断解

取决于矩阵的形状
1. 完美阶梯形 —— 唯一解

每一个未知数对应一个常数，因此只有一个解

2. $0=k(k\ne 0)$ —— 无解

矩阵中有一个方程未知数的系数为0，而右侧的常数非0，则$0\ne 0$，无解

3. $0=0$ —— 无数解

矩阵中有一个方程左右两侧都是0，则未知数可以取任意值，有无数解

想法

将原方程组化成矩阵，例如

\[\left\{ $$\begin{array}{c}{x}_1+2x_2-x_3=-6\\ 2x_1+x_2-3x_3=-9\\ -x_1-x_2+2x_3=7\\ \end{array}$$ \right. \]

可以转化为

$$\left(\begin{array}{cccc}1& 2& -1& -6\\ 2& 1& -3& -9\\ -1& -1& 2& 7\\ \end{array}\right)$$

然后运用高斯消元进行变形，模拟：

第一次迭代

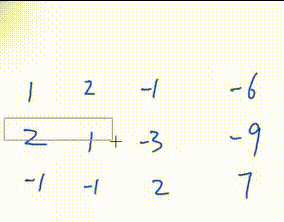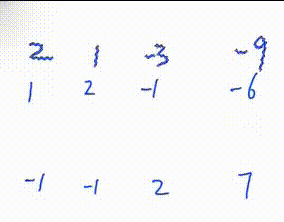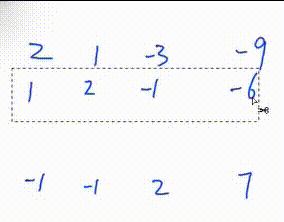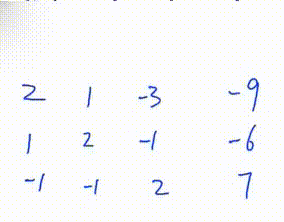
1. 找到绝对值最大的一行
2. 将该行移到最上面

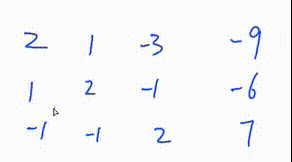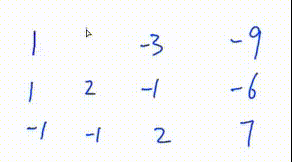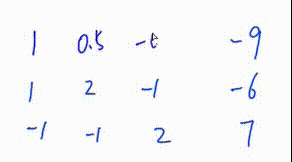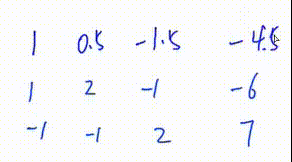
3. 将该行第一个数变为1

此处是将第一行所有数乘$\frac{1}{2}$

初等行变换$1.$

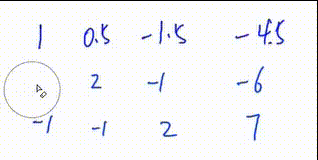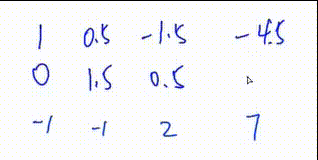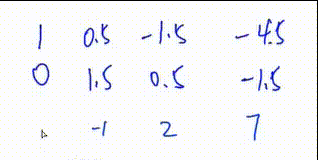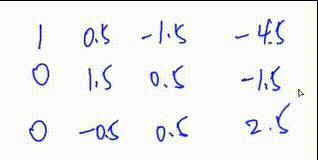
4.将第一行下面所有行的第$c$列变成0

此GIF中第一次操作 将第二行减去第一行的一倍

初等行变换$3.$

第二次操作 将第三行加上第一行的一倍

初等行变换$3.$

第二次迭代

注意：做完第一次迭代时，第一行就固定了，因此只需要从下面开始即可

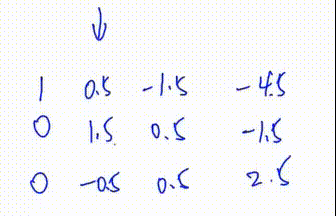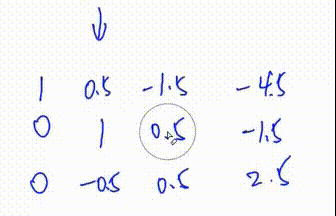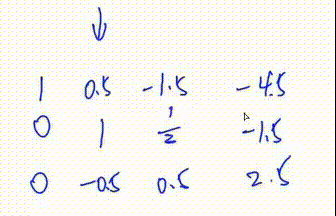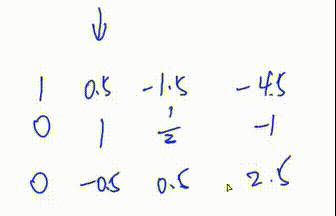
此处第三列y总笔误，应是$\frac{1}{3}$而不是$\frac{1}{2}$

1. 找到绝对值最大的一行
2. 将第二行行移到最上面

此时第二行本身就符合1.2.的要求，因此不用动

3. 将第二行第一个数变为1

即 将第二行乘以$\frac{2}{3}$

初等行变换$1.$

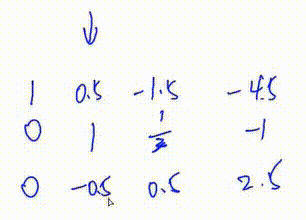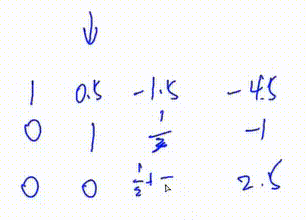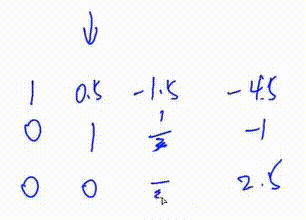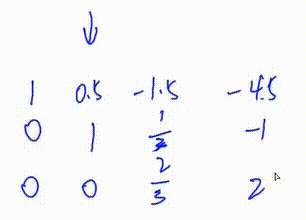
4.将第一行下面所有行的第$c$列变成0

此处将第三行加上$\frac{1}{2}$倍的第二行

初等行变换$3.$

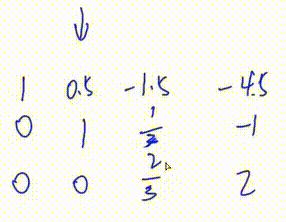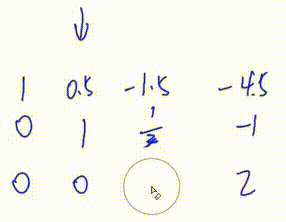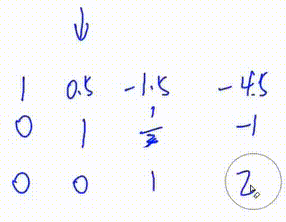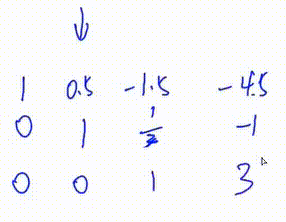
3. 将第三行第一个数变为1

即 将第三行乘以$\frac{3}{2}$

解方程

我们发现这是一个完美的阶梯形矩阵，因此该方程组有唯一解
矩阵

$$\left(\begin{array}{cccc}1& \frac{1}{2}& -\frac{3}{2}& -\frac{9}{2}\\ 0& 1& \frac{1}{3}& -1\\ 0& 0& 1& 3\\ \end{array}\right)$$

化成方程组的形式：

$$\{\begin{array}{rl}{x}_1+\frac{1}{2}{x}_2-\frac{3}{2}{x}_3& =-\frac{9}{2}\\ x_2+\frac{1}{3}{x}_3& =-1\\ x_3& =3\\ \end{array}$$

我们发现$x_3$在消元的过程中已经解出来了，要解②就只需要将$\mathrm{③}\times \frac{1}{3}$得
$\frac{1}{3}=1\mathrm{④}$
然后用$\mathrm{②}-\mathrm{④}$，得：

$$\{\begin{array}{rl}{x}_1+\frac{1}{2}{x}_2-\frac{3}{2}{x}_3& =-\frac{9}{2}\\ x_2& =-2\\ x_3& =3\\ \end{array}$$

即

$$\left(\begin{array}{cccc}1& \frac{1}{2}& -\frac{3}{2}& -\frac{9}{2}\\ 0& 1& 0& -2\\ 0& 0& 1& 3\\ \end{array}\right)$$

对①进行同样的操作，解得

$$\{\begin{array}{rl}{x}_1-\frac{3}{2}{x}_3& =-\frac{7}{2}\\ x_2& =-2\\ x_3& =3\\ \end{array}$$

$$\left(\begin{array}{cccc}1& 0& -\frac{3}{2}& -\frac{7}{2}\\ 0& 1& 0& -2\\ 0& 0& 1& 3\\ \end{array}\right)$$

再消去$x_3$：

$$\{\begin{array}{rl}{x}_1& =1\\ x_2& =-2\\ x_3& =3\\ \end{array}$$

也就是

$$\left(\begin{array}{cccc}1& 0& 0& 1\\ 0& 1& 0& -2\\ 0& 0& 1& 3\\ \end{array}\right)$$

码来！

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath> // fabs() = float abs = 浮点数的绝对值，相对应的，整数的绝对值即为abs()
using namespace std;

const int N = 110;
const double eps = 1e-8; // 防止出现精度问题

double a[N][N];
int n;

int gauss()
{
    int c = 0, r = 0;
    for(; c < n; c++)
    {
        int t = r;
        for (int i = r; i < n; i ++ ) // 第一步，找绝对值最大的行
        {
            if(fabs(a[i][c]) > fabs(a[t][c]))
                t = i; 
        }
        
        if(fabs(a[t][c]) < eps) continue; // 代表这一列已经被处理过了
         
        for(int i = c; i <= n; i++) // 第二步 
            swap(a[t][i], a[r][i]); // 将这一行调到最上面
            
        for(int i = n; i >= c; i--) // 第三步
            a[r][i] /= a[r][c]; // 要倒着算，否则会影响后面的数
        
        for(int i = r + 1; i < n; i++) // 第四步
        {
            if(fabs(a[i][c]) > eps)  // 如果是0就不用操作了
            {
                for(int j = n; j >= c; j--)
                {
                    a[i][j] -= a[r][j] * a[i][c];
                }
            }
        }
        r++;
    }
    
    if(r < n) // 方程数 < n
    {
        for(int i = r; i < n; i++)
        {
            if(fabs(a[i][n]) > eps) // 0 != 0
            {
                return 2; // 无解
            }
        }
        
        return 1; // 无数解, 0=0
    }
    
    for(int i = n - 1; i >= 0; i --) // 有解从下往上回代
    {
        for(int j = i + 1; j < n; j++)
        {
            a[i][n] -= a[i][j] * a[j][n];
        }
    }
    return 0;
    
}


int main()
{
    scanf("%d", &n);
    
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n + 1; j ++ )
            scanf("%lf", &a[i][j]);
    
    int t = gauss();
    
    if(t == 0)  // 有唯一解
    {
        for (int i = 0; i < n; i ++ )
        {
            if(fabs(a[i][n]) < eps) a[i][n] = 0.00; // 避免输出-0.00
            printf("%.2lf\n", a[i][n]);
            
        }
    }
    
    else if(t == 1) puts("Infinite group solutions"); // 无数解
    else puts("No solution"); // 无解
    
}