欧拉函数

给定 \(n\) 个正整数 \(a_i\)，请你求出每个数的欧拉函数。

欧拉函数的定义

$ 1 \sim N $ 中与 $ N $ 互质的数的个数被称为欧拉函数，记为 $ ϕ(N) \(。 若在算数基本定理中，\) N = p_1^{a_1}p_2…p_m^{a_m} \(，则： \) ϕ(N) $ = $ N \times \frac{p_1-1}{p_1} \times \frac{p_2-1}{p_2} \times … \times \frac{p_m-1}{p_m} $

想法

欧拉函数是什么？

$ ϕ(N) $ = $ N \times \frac{p_1-1}{p_1} \times \frac{p_2-1}{p_2} \times … \times \frac{p_m-1}{p_m} $

\(p_i\)是N的质因数

证明

通过容斥原理证明

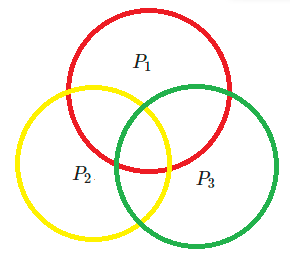
设\(N\)只有三个质因子\(P_1P_2P_3\)，如图，整个图表示\(N\)因数的集合，\(P_1P_2P_3\)所在的红、黄、绿三圈分别表示\(P_1P_2P_3\)倍数的集合（\(\frac{N}{P_1} + \frac{N}{P_2}+\frac{N}{P_3}\)）
这些三个集合中的所有数都与\(N\)有共同的质因子，换句话说，\(1到N\)中除去这三个集合的所有数都与\(N\)互质
但是其中有的数既在\(P_1\)中又在\(P_2\)中，这些重复减去的数要加上
但是但是其中有的数既在\(P_1P_2\)又在\(P_3\)中，这些重复加上的数要减去

容斥原理

因此

\[\phi(N) = N - \frac{N}{P_1} - \frac{N}{P_2} - \frac{N}{P_3} + \frac{N}{P_1P_2} + \frac{N}{P_1P_3} + \frac{N}{P_2P_3} - \frac{N}{P_1P_2P_3} \]

\[\phi(N) = N \times (1 - \frac{1}{P_1} - \frac{1}{P_2} - \frac{1}{P_3} + \frac{1}{P_1P_2} + \frac{1}{P_1P_3} + \frac{1}{P_2P_3} - \frac{1}{P_1P_2P_3}) \]

\[\phi(N) = N \times (1 - \frac{1}{P_1}) \times (1 - \frac{1}{P_2}) \times (1 - \frac{1}{P_3}) \]

\[ \phi(N) = N \times \frac{P_1-1}{P_1} \times \frac{P_2-1}{P_2} \times \frac{P_3 - 1}{P_3} \]

这是三个质因数的情况，推广到\(m\)个质因数

\[ \phi(N) = N \times \frac{P_1-1}{P_1} \times \frac{P_2-1}{P_2} \times \dots \times \frac{P_m-1}{P_m} \]

代码

#include <iostream>

using namespace std;

int main()
{
    int n;
    cin >> n;
    
    while (n -- )
    {
        int x, res;
        cin >> x;
        
        res = x;
        
        // 分解质因数的时候顺便求一下欧拉函数
        for(int i = 2; i <= x / i; i++)
        {
            if(x % i == 0)
            {
                res = res / i * (i - 1); // 公式
                
                while(x % i == 0) x /= i;
            }
        }
        
        if(x > 1) res = res / x * (x - 1); // 公式
        
        cout << res << endl;
    }
    return 0;
}