状态压缩DP

概念

1. 什么是状态压缩

状态压缩顾名思义便是把一大堆状态压缩成二进制数，节省了空间

2. 如何状态压缩

用$int$类型来存储二进制数，再用位运算进行计算

例题

1. 最短Hamilton路径

题意：求一笔画一张无权图的长度的最小值

思路：通过枚举从i经过所有点到j的情况长度，求出最小值

闫氏dp分析法：

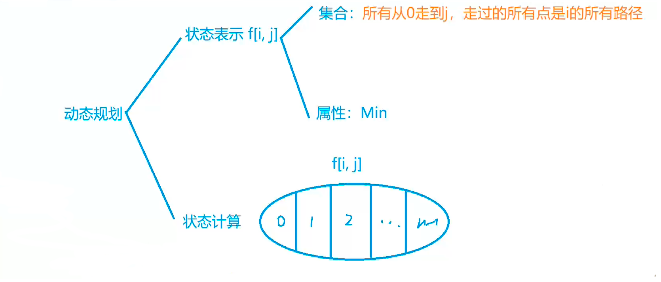
其中$i$是二进制的状态，$j$是目前到了的点

状态转移方程：
$f[i][j]=min(f[i][j],f[i-(1<<j)][k]+g[k][j])$

$i-(1<<j)$ 表示除去$j$后的所有路径 —— 1 << j用二进制表示就是$00\cdots 010\underset{j\mathrm{个}0}{\underbrace{\cdots 0}}$
$f[i-(1<<j)][k]+g[k][j]$ 就是从i到k的最短长度加上k到j的路程

码来！

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 20, M = 1 << N; // state需要的空间+1

int f[M][N], g[N][N], n; // 邻接矩阵存储图

int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i++)
        for (int j = 0; j < n; j ++ )
            scanf("%d", &g[i][j]);
    
    memset(f, 0x3f, sizeof f); // 普通的初始化
    f[1][0] = 0; // 对于起点路程是0
    
    for(int i = 0; i < 1 << n; i++) // 枚举所有状态
        for (int j = 0; j < n; j ++ ) // 枚举所有当前点
            if(i >> j & 1) // 判断j是否走过
                for(int k = 0; k < 0; k++) // 枚举所有要经过的点
                    if(i >> k & 1) // 判断k是否走过
                        f[i][j] = min(f[i][j], f[i - (1 << j)][k] + g[k][j]); // 状态转移方程
    
    printf("%d", f[(1 << n) - 1][n - 1]);
    return 0;
}

2. 蒙德里安的梦想

题意：求用1*2的长方形去填一个棋盘的方案数

思路：一列一列枚举，看每一列中有多少个合法的方案

闫氏dp分析法：

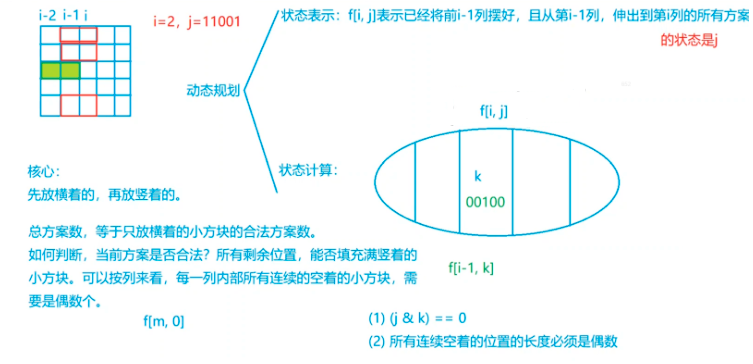
状态转移方程：$f[i][j]+=f[i-1][k]$

即枚举上一列的状态（k）所有的可能情况
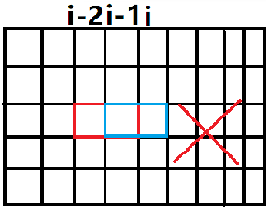
注意：需要判断情况的合法性，如图，当从第$i-2$列伸到第$i-1$列的方块是躺着的，从第$i-1$列伸到第$i$列的方块也是躺着的时，就会重叠，也就是$(j\mathrm{\&}k)==0$时才是合法的

两数进行&运算时，只有每一位相同结果才是0
$j|k$表示$i-1$到$i$的状态和$i-2$到$i-1$的状态总共有多少个1，$st[j|k]$则用于判断i-1这一行是否合法

暴力代码：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 12, M = 1 << N;

long long f[N][M];
bool st[M];
int n, m;

int main()
{
    while(cin >> n >> m, n || m)
    {
        for (int i = 0; i < 1 << n; i ++ )
        {
            int cnt = 0; // cnt统计连续0的个数，如果有奇数个0就是不合法情况
            st[i] = true; // st[]相当于记录每一列的cnt
            for (int j = 0; j < n; j ++ )
            {
                if(i >> j & 1) // 如果i的第j位是1，也就是第j行有伸出来的方格
                {
                    if(cnt % 2 == 1)
                    {
                        st[i] = false; // 当0的个数是奇数时就记录下来这种情况不合法，也可以写为cnt & 1
                        break;
                    }
                    cnt = 0; // 判断过一段了就可以从0开始重新统计
                }
                else cnt ++; // 因为i的第j位是0所以cnt++
            }
            if(cnt % 2 == 1) st[i] = false; // 在末尾还要进行一次判断，避免错过最后一段连续的0
        }
        memset(f, 0, sizeof f); // 将所有状态初始化为0
    
        f[0][0] = 1; // 回顾集合定义，由于第-1列不存在所以自然而然地只有一种方案 —— 全立着
    
        for(int i = 1; i <= m; i++) // 枚举列
        {
            for(int j = 0; j < 1 << n; j ++) // 枚举i-1到i的状态
            {
                for (int k = 0; k < 1 << n; k ++ ) // 枚举i-2到i-1的状态
                {
                    if((j & k) == 0 && st[j | k]) // 如果是合法的
                        f[i][j] += f[i-1][k]; // 状态转移
                }
            }
        }
    
        cout << f[m][0] << endl;
        // 回顾集合定义：
        // f[m][0]代表m-1已经确定，从m-1伸向m的状态是00000，也就是没有伸向m的方块，棋盘只有0~m-1列
    }
    
    
    return 0;
}

进行一个小优化：预处理每一次的合法状态，最后直接用就好了

码来！

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 12, M = 1 << N;

long long f[N][M];
vector<int> state[M]; // 这个数组预处理存储合法状态
bool st[M];
int n, m;

int main()
{
    while(cin >> n >> m, n || m)
    {
        for (int i = 0; i < 1 << n; i ++ )
        {
            int cnt = 0;
            bool &isValid = st[i]; // 引用
            isValid = true;
            for (int j = 0; j < n; j ++ )
            {
                if(i >> j & 1)
                {
                    if(cnt % 2 == 1)
                    {
                        isValid = false;
                        break;
                    }
                    cnt = 0;
                }
                else cnt ++;
            }
            if(cnt % 2 == 1) isValid = false;
        }
        
        // ========这就是优化的东西=========
        for(int i = 0; i < 1 << n; i++) // 预处理合法状态
        {
            state[i].clear(); // 每组数据的state是独立，所以每次都要清除一遍
            for(int j = 0; j < 1 << n; j++)
            {
                if((i & j) == 0 && st[i | j]) // 此处只是把原来的j和k改成了此处的i和j
                    state[i].push_back(j); // 把合法的j推进去
            }
        }
        // ========这就是优化的东西=========
        
        
        memset(f, 0, sizeof f);
    
        f[0][0] = 1;
    
        for(int i = 1; i <= m; i++)
        {
            for(int j = 0; j < 1 << n; j ++)
            {
                for (auto k : state[j]) // 此处遍历之前预处理的数组
                {
                    
                    f[i][j] += f[i-1][k];
                }
            }
        }
    
        cout << f[m][0] << endl;
    }
    
    
    return 0;
}

题图也是Hamilton，谐音梗（（（（别打我