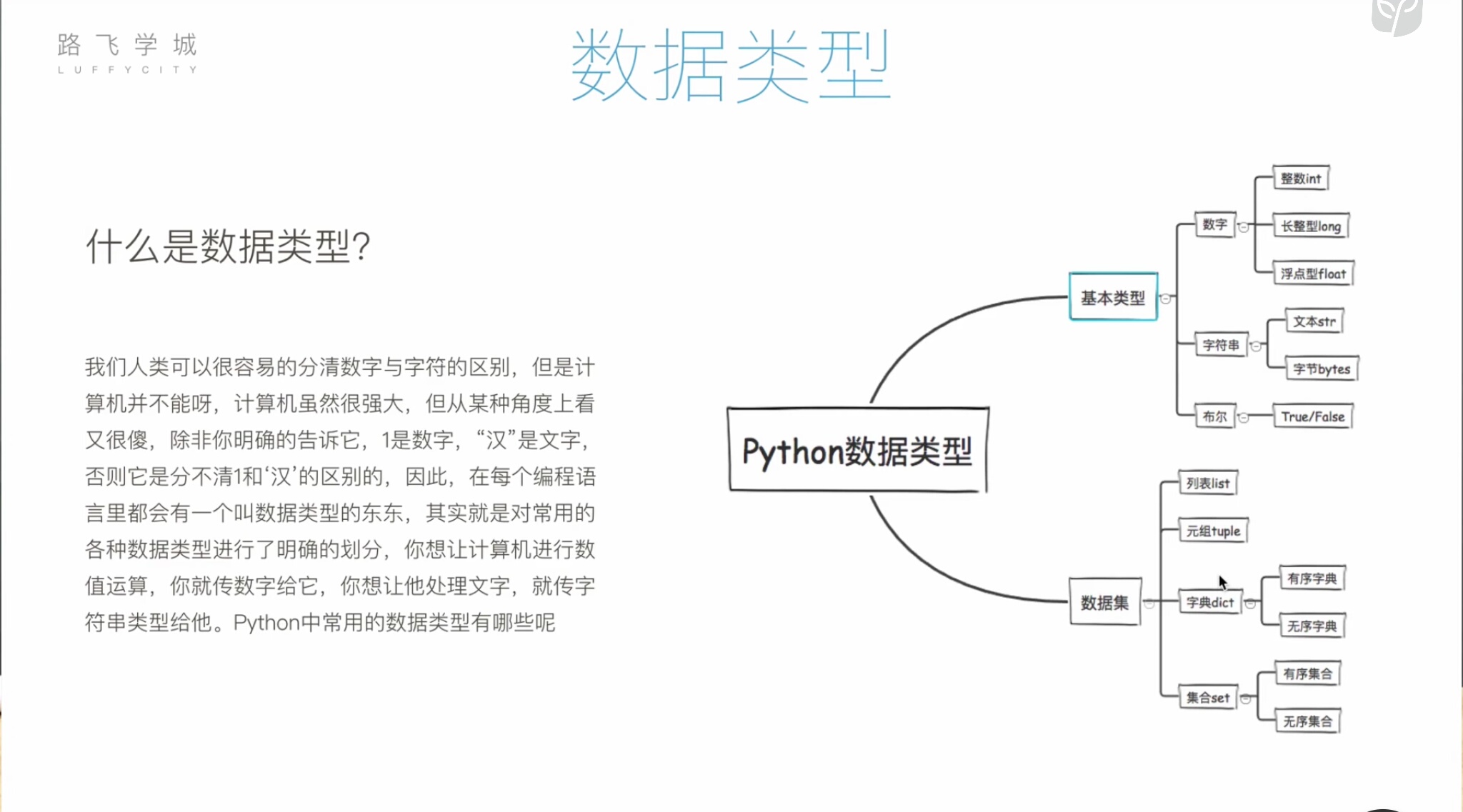
1.定义时不需要像C语言一样加 ' int ' , 'char ' 等,直接写即可,解释器会直接自动识别数据类型。例: age = 22 (默认为数字类型) name = 'Alex' (默认为字符串类型)
2.字符串类型:Python中,加了引号的都被认为是字符串!
(1)单引号和双引号没区别,在句子里出现单引号时,外面只能是双引号,例: “ What‘s your name : "
(2)多引号用于多行的一段话,例: ’‘’ 今天我想写首诗
歌颂我的同桌,
你看他那乌黑的短发,
好像一只炸毛鸡。 '''
(3)不加引号的字符串被认为是变量,例: name = Jack 会报错 NameError :'Jack' is not defined.
(4)字符串拼接:字符串可以进行"相加"、"相乘"运算,"相加"就是简单的拼接到一起,"相乘"就是将字符串重复多少遍并且拼接起来,字符串只能和字符串进行运算,不能和数字等其他数据类型进行运算。
3.布尔类型:很简单,就两个值,一个True(真),一个False(假),用来做后面的逻辑运算。
4.格式化输出:用占位符,%s是string字符串类型,%d是digit数字类型,%f是float小数类型,所有的input后面的都默认是字符串类型,想转换成数字就用 A = int ( input ( ……) ) 这样转换之后,A就是数字类型了。
name = input ("Name:") age = input("Age:") job = input("Job:") hometown = ("Hometown:") #print('-----------info of ',name,'-----------') #print('Name: ',name) #print('Age:',age) #print('Job:',job) #print('Homeown:',hometown) #print('----------end----------------') info = ''' -----------info of %s ------------ Name: %s Age: %s Job: %s Hometown: %s -------------end------------------ ''' % (name,name,age,job,hometown)
5.运算符:
(1)算术运算: +加 、 -减 、 *乘 、 /除 、 %余数 、**幂 、 //取整除
(2)比较运算:==等于 、 !=不等于(和<>类似) 、 >大于 、 <小于 、 >=大于等于 、 <=小于等于
(3)逻辑运算:and与 、 or或 、 not非
(4)赋值运算
6.二进制转换 bin ( 要转换的数字 )
7.ASCII 每一位0或1所占空间为位(bit),这是计算机中最小的表示单位。
8bit = 1bytes(字节) 1KB = 1024B 1MB = 1024KB 1GB = 1024MB 1TB = 1024GB 1PB = 1024TB 1EB = 1024PB 1ZB = 1024EB 1YB = 1024ZB 1BB = 1024YB
8.浮点数和科学记数法
(1)科学记数法( scientific notation):科学记数法是指把一个数表示成ax10的n(1<=n<10,n为正整数)次幂的形式。例如19971400000000=1.99714x10**13.计算器或电脑表达10的幂一般是用E或e,也就是1.99714E13=19971400000000。用幂的形式,有时可以方便地表示日常生活中遇到的一些较大的数。
(2)复数:复数指能写成如下形式的数a+bi,这里a和b是实数,i是虚数单位(即-1开根)。在复数a+bi中,a称为复数的实部,b称为复数的虚部,i称为虚数单位。当虚部等于零时,这个复数称为虚数。在Python中(-5+4j)和(2.3-4,6j)是复数的例子,其中-5,4为实数,j为虚数,而在数学中i为虚数。
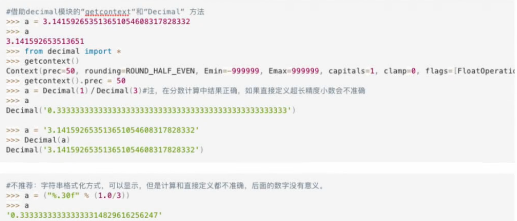
(3)浮点数(小数)精度为17位,也就是小数点后16位,尽管有16位,但是这个精确度却是越往后越不准的。这个问题不只是存在于Python中,其他语言也有同样问题。原因和浮点数存储结构有关。
计算高精确度的浮点数方法