【数理统计】分位数

目录

• 上分位数和下分位数的定义
  • 下分位数的直观理解
  • 上分位数的直观理解
• 常用分布中的分位数
  • 正态分布
  • 卡方分布

上分位数和下分位数的定义

设连续型随机变量 \(X\) 的分布函数为 \(F(x)\)，概率密度函数为 \(f(x)\)，则：

• 对于任意正数 \(\alpha(0<\alpha<1)\)，称满足条件

\[F(x_{\underline{\alpha}}) = \int_{-\infty}^{x_{\underline{\alpha}}} f(x)dx = \alpha \]

的数为此分布的 \(\alpha\) 分位数或下 \(\alpha\) 分位数。

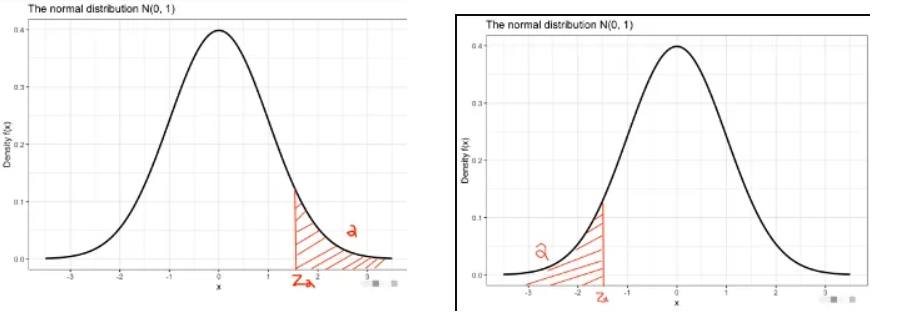
理解下 \(\alpha\) 分位数：从 \(x_{\alpha}\) 这个点把分布函数图像切成两个部分，左边部分面积占比 \(\alpha\)，右边部分面积占比 \(1-\alpha\)。（下图右图）

• 对于任意正数 \(\alpha(0<\alpha<1)\)，称满足条件

\[1-F(x_{\alpha}) = \int_{x_{\alpha}}^{+\infty} f(x)dx = \alpha \]

的数为此分布的上 \(\alpha\) 分位数。

理解上 \(\alpha\) 分位数：从 \(x_{\alpha}\) 这个点把分布函数图像切成两个部分，左边部分面积占比 \(1-\alpha\)，右边部分面积占比 \(\alpha\)。（下图左图）

上分位数和下分位数的关系如下：

• \(x_{\underline{\alpha}} = x_{1-\alpha}\)
• \(x_{\alpha} = x_{\underline{1-\alpha}}\)

下分位数的直观理解

分位数是数理统计中用来描述数据分布的一种统计量，它将数据集分成若干个部分，使得每个部分包含相同数量的数据点。常见的分位数包括中位数（50%分位数）、四分位数（25%和75%分位数）等。

• 中位数（Median）：将数据分成两部分，中位数是数据中间的值，50%分位数。
• 四分位数（Quartiles）：
  • 第一四分位数（Q1）：将数据下25%的点分开。
  • 第二四分位数（Q2）：即中位数（50%分位数）。
  • 第三四分位数（Q3）：将数据上25%的点分开。

假设有以下一组数据：

数据集：3, 7, 8, 12, 14, 18, 20

1. 计算中位数：

   • 排序后的数据为：3, 7, 8, 12, 14, 18, 20
   • 中位数（Q2）是中间的值，即 12。

2. 计算四分位数：

   • 第一四分位数（Q1）：前半部分数据是 3, 7, 8，中位数是 7。
   • 第三四分位数（Q3）：后半部分数据是 14, 18, 20，中位数是 18。

上分位数的直观理解

上分位数（Upper Quantile）：一个分位数 \(q\) 的上分位数是指使得有 \(1 - q\) 的数据点小于该分位数的值。

常见的上分位数：

• 上四分位数（Q1）：表示25%数据点大于该值，75%数据点小于该值。
• 上中位数：在中位数（Q2）中，50%的数据点大于该值。
• 上95%分位数（即95th Percentile）：表示有5%的数据点大于该值，95%的数据点小于该值。

假设我们有一组数据，表示某个考试的分数：

数据集：55, 60, 65, 70, 75, 80, 85, 90, 95, 100

计算上分位数：

• 上四分位数（Q1）：

  • Q1 = 65（25%的数据点大于65）。

• 上中位数（Q2）：

  • Q2 = 75（50%的数据点大于75）。

• 上95%分位数：

  • 95th Percentile = 95（5%的数据点大于95）。

常用分布中的分位数

不同分布的符号简写：

• b：二项分布
• p：泊松分布
• u：标准正态分布
• e：指数分布
• z：正态分布（不一定是标准的）

正态分布

标准正态分布表

若 \(X \sim N(0,1)\) 即服从标准正态分布，则分布函数记为 \(\Phi(x)\)。由标准正态分布的对称性可知：\(\Phi(-x) = 1-\Phi(x)\)。显然，\(P \{ x_1 < X < x_2 \} = \Phi(x_2) - \Phi(x_1)\)。

• 对于上分位数 \(u_{\alpha}\)，有 \(\Phi(u_{\alpha}) = 1 - \alpha\)
• 对于下分位数 \(u_{\alpha}\)，有 \(\Phi(u_{\alpha}) = \alpha\)
• 上下分位数之间的关系有 \(u_{\alpha} = -u_{1-\alpha}\)（仅标准正态分布成立）

对于自由度为 \(n\) 的 t 分布也有类似的结论：\(t_{\alpha}(n) = -t_{1-\alpha}(n)\)。当 \(n (n>45)\) 足够大时，有：\(t_{\alpha}(n) \approx u_{\alpha}\)

标准正态分布中常见的分位数：

• 0.25分位数（第一四分位数 Q1）：约为 -0.6745，即 \(u_{0.25} = -u_{0.75} \approx -0.6745\)
• 0.50分位数（中位数 Q2）：为 0，即 \(u_{0.50} = 0\)
• 0.75分位数（第三四分位数 Q3）：约为 0.6745，即 \(u_{0.75} \approx 0.6745\)

假设我们有一组服从正态分布 \(N(100, 15^2)\) 的随机变量，即均值为100，标准差为15。我们可以计算这些变量的分位数。

• 25%分位数（Q1）：

  • 使用标准正态分布的Q1值：约为 -0.6745。
  • 实际分位数计算：Q1 = 100 + (-0.6745 × 15) ≈ 90.87。

• 50%分位数（Q2）：

  • 使用标准正态分布的Q2值：为 0。
  • 实际分位数计算：Q2 = 100 + (0 × 15) = 100。

• 75%分位数（Q3）：

  • 使用标准正态分布的Q3值：约为 0.6745。
  • 实际分位数计算：Q3 = 100 + (0.6745 × 15) ≈ 109.12。

卡方分布

若 \(\chi^2 \sim \chi^2(n)\)，则上分位数 \(\chi^2_{\alpha}\) 是满足以下条件的值：

\[P \{ \chi^2 > \chi^2_{\alpha}(n) \} = \alpha \]

这意味着有 \(1-\alpha\) 的概率观测值会大于该上分位数值。

上分位数的应用：

1. 假设检验：在卡方检验中，通常使用上分位数来决定拒绝域。例如，在检验两个分类变量的独立性时，可以使用卡方统计量与上分位数进行比较。
2. 置信区间：在构建卡方分布的置信区间时，也会使用上分位数。

假设我们有一个卡方分布 \(\chi^2 \sim \chi^2(5)\)，即自由度 \(n = 5\)，我们想找出上5%分位数（\(\alpha=0.05\)，即95%分位数）：

• 查卡方分布表，找到自由度为5时，与0.95对应的上分位数 \(\chi^2_{0.05}\)。
• 结果为大约 11.070。

这意味着在自由度为5的卡方分布中，有5%的概率观察到的值会大于11.070。类似的还有 F 分布中的上分位数，此处不再赘述。