拟牛顿法的思想
牛顿法的迭代方程为:
dk=−(∇2f(xk))−1∇f(xk)
牛顿法的优缺点:
- 优点:局部二阶收敛,速度快。
- 缺点:每步都要计算 Hessian 矩阵 ∇2f(xk),运算量大,还要求函数至少二阶连续可微。
拟牛顿法的核心思想:每步用 Bk 近似取代 ∇2f(xk),其满足以下条件:
- 某种意义下,Bk≈∇2f(xk)
- Bk 对称且正定,以产生下降方向(即保持下降性)
- Bk 的更新与计算要简单,只需函数的一阶信息
拟牛顿法的条件
设 f(x) 是二阶连续可微函数,对 ∇f(x) 在点 xk+1 处进行一阶泰勒近似:
∇f(x)≈∇f(xk+1)+∇2f(xk+1)(x−xk+1)
令 x=xk,则:
∇f(xk+1)−∇f(xk)≈∇2f(xk+1)(xk+1−xk)
记:
- 位移差:sk=xk+1−xk
- 梯度差:yk=∇f(xk+1)−∇f(xk)
由此得到:
∇2f(xk+1)sk≈yk
由拟牛顿法的思想,我们希望 Bk+1 满足:
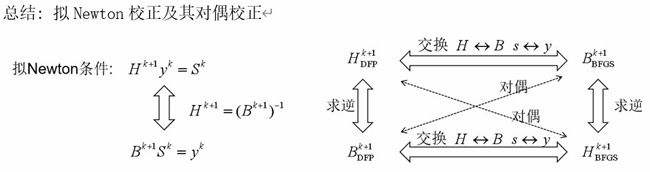
Bk+1sk≈yk
令 Hk+1=B−1k+1,则有:
Hk+1yk≈sk
上述两个方程又被称为割线方程。
拟牛顿法的步骤
拟牛顿法:
- 第一步:选取初始点 x0,H0=I,给定终止误差 ε>0 ,令 k=0
- 第二步:计算 ∇f(xk),若 ||∇f(xk)||≤ε,停止迭代并输出 x∗=xk;否则进行第三步
- 第三步(搜索方向):计算搜索方向 dk=−Hk∇f(xk)
- 第四步(迭代更新):计算 xk+1=xk+dk
- 第五步(更新 Hk):计算 Hk+1=g(Hk)
拟阻尼牛顿法:
- 第一步:选取初始点 x0,H0=I,给定终止误差 ε>0 ,令 k=0
- 第二步:计算 ∇f(xk),若 ||∇f(xk)||≤ε,停止迭代并输出 x∗=xk;否则进行第三步
- 第三步(搜索方向):计算搜索方向 dk=−Hk∇f(xk)
- 第四步(线搜索):通过线搜索确定步长 αk
- 第五步(迭代更新):计算 xk+1=xk+αkdk
- 第六步(更新 Hk):计算 Hk+1=g(Hk)
现在的关键要点是:如何更新 Hk 且保持其对称正定性以及计算简单?想法如下:
Hk+1=Hk+Dk或Bk+1=Bk+Ek
其中要求 Dk 或 Ek 的生成要尽量简单,被称为校正矩阵。
校正矩阵的确定
SR1 校正(对称秩 1 校正)
为保证 Dk 是秩 1 矩阵且 Hk 对称,可设 Dk=αuu⊤。将该式带入到割线方程中,经过一系列推导后可得 SR1 校正公式:
Hk+1={Hk+(sk−Hkyk)(sk−Hkyk)⊤(sk−Hkyk)⊤yk, 若(sk−Hkyk)⊤yk≠0Hk, 若(sk−Hkyk)⊤yk=0
其对偶式为:
Bk+1=Bk+(yk−Bksk)(yk−Bksk)⊤(yk−Bksk)⊤sk
注:
- SR1 校正产生的 Hk+1 满足对称性,但不一定正定,即搜索方向不一定是下降的;
- 无法保证 (sk−Hkyk)⊤yk>0,导致 Hk+1 可能非正定。
DFP 校正
Hk+1 由 Hk 经对称秩 2 校正产生,即 Dk=αuu⊤+βvv⊤。将该式带入到割线方程中,经过一系列推导后可得 DFP 校正公式:
Hk+1=Hk+sks⊤ks⊤kyk−Hkyk(Hkyk)⊤y⊤Hkyk
DFP 校正产生的 Hk+1 满足对称性且正定。
注:
- s⊤kyk>0 在实际应用中是容易满足的条件:
- 采用精确线搜索和非精确的 Wolfe-Powell 准则时,条件一定满足;
- 采用非精确的 Armijo-Goldstein 准则时,条件可能不满足,当不满足时直接令 Hk+1=Hk;
- 当求解大规模非线性优化时,Hk 可能越来越接近奇异矩阵,使得算法“卡住”;
- 如果求解二次正定优化问题时,令 H0=I,则 DFP 算法是共轭梯度法。
BFGS 算法
与 DFP 的校正思路和过程类似,但 BFGS 构造的是 Bk+1,经过一系列推导后可得到 BFGS 的校正公式:
Bk+1=Bk+yky⊤ky⊤ksk−Bksk(Bksk)⊤s⊤Bksk
BFGS 校正产生的 Bk+1 满足对称性且正定。
注:
- y⊤ksk>0 在实际应用中是容易满足的条件:
- 采用精确线搜索和非精确的 Wolfe-Powell 准则时,条件一定满足;
- 采用非精确的 Armijo-Goldstein 准则时,条件可能不满足,按如下公式进行更新(此式有现成图片,就懒得自己打一遍了):
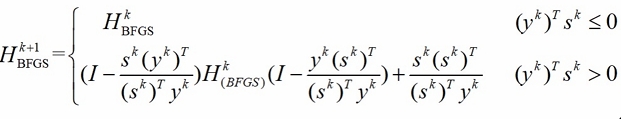
- 实际应用中,BFGS 更新 Hk,通过 dk+1=−Hk+1∇f(xk+1) 产生下降方向。
- BFGS 和 DFP 形式上是对偶的:
本文作者:漫舞八月(Mount256)
本文链接:https://www.cnblogs.com/Mount256/p/18601495
版权声明:本作品采用CC 4.0 BY-SA许可协议进行许可。
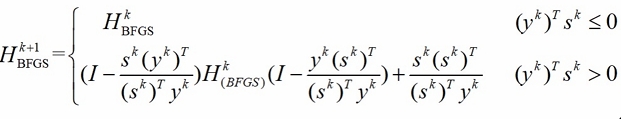





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异
· 三行代码完成国际化适配,妙~啊~
2022-12-12 【数据结构-树】二叉树的相关算法