【最优化方法】第三次要点整理

目录

• 非精确线搜索技术
• Armijo-Goldstein 准则
• Wolfe-Powell 准则
• 强 Wolfe-Powell 准则

【问题】在迭代中，已知 \(x^{(k)}\) 和下降方向 \(d^{(k)}\)，如何确定下降步长 \(\alpha^{(k)}\)，使得 \(f(x^{(k)} + \alpha^{(k)} d^{(k)}) < f(x^{(k)})\)？

非精确线搜索技术

求 \(\alpha^{(k)}\)，使得 \(\Delta f_k = f(x^{(k)}) - f(x^{(k)} + \alpha^{(k)} d^{(k)}) > \epsilon\)，即保证 \(f(x)\) 在每一步都有满意的下降，而不必精确计算梯度，从而大大节省计算量。

\[J = \{ \alpha > 0 \ | \ f(x_k + \alpha_k d_k) < f(x_k) \} \]

Armijo-Goldstein 准则

【思想】我们希望优化算法满足以下两个条件：

1. 目标函数要有足够的下降，使得 \(f(x_{k+1}) < f(x_k)\)；
2. 步长 \(\alpha^{(k)}\) 不能太小，保证每步都要有更新，否则就会出现 \(f(x_{k+1}) \approx f(x_k)\) 的情况。

由第一个条件可得：

\[\begin{aligned} f(x_k + \alpha_k d_k) \leq f(x_k) + \alpha \rho \nabla f(x_k)^\top d_k \\ 或写成：\varphi(\alpha) \leq \varphi(0) + \alpha \rho \varphi'(0) \end{aligned} \]

由第二个条件可得：

\[\begin{aligned} f(x_k + \alpha_k d_k) \geq f(x_k) + \alpha (1-\rho) \nabla f(x_k)^\top d_k \\ 或写成：\varphi(\alpha) \geq \varphi(0) + \alpha (1-\rho) \varphi'(0) \end{aligned} \]

其中 \(0 < \rho < \frac{1}{2}\)，保证了 \(\alpha (1-\rho) \varphi'(0) < \alpha \rho \varphi'(0) < 0\)。由下图知：

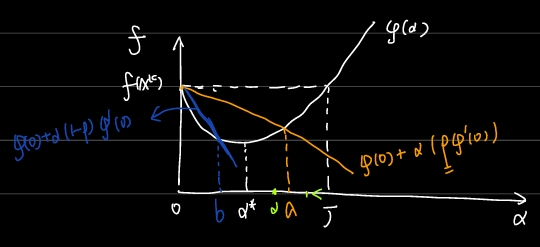
满足第一个条件的 \(\alpha\) 构成区间 \((0, a]\)，满足第二个条件的 \(\alpha\) 构成区间 \([b, J]\)，因此两个条件构成的约束为 \(\alpha \in [b, a]\)。

【算法步骤】由以上思想可得 Goldstein 准则非精确先搜索算法：

初始值设为 \(a_1=0, a_2=M, \alpha>0\)，

• 第一步：计算 \(\varphi(0), \varphi'(0)\)，在区间 \([0, M]\) 上选取初始点 \(\alpha\)。
• 第二步：计算 \(\varphi(\alpha)\)。
• 第三步：检查 \(\varphi(\alpha) \leq \varphi(0) + \alpha \rho \varphi'(0)\) 是否满足，若满足则进行第四步；否则 \(a_2 \leftarrow \alpha, \alpha \leftarrow \frac{a_1 + a_2}{2}\)，返回第二步。
• 第四步：检查 \(\varphi(\alpha) \geq \varphi(0) + \alpha (1-\rho) \varphi'(0)\) 是否满足，若满足则输出 \(\alpha_k = \alpha\)，结束迭代；否则 \(a_1 \leftarrow \alpha, \alpha \leftarrow \frac{a_1 + a_2}{2}\)，返回第二步。

Wolfe-Powell 准则

Goldstein 准则有一个很大的问题是约束区间不一定存在想要的最优点，即 \([b, a]\) 可能把 \(\alpha^*\) 排除在外。为克服上述缺陷，Wolfe 提出了使用以下的条件来代替 Goldstein 中的第二个条件：

\[\begin{aligned} \nabla f(x_k + \alpha_k d_k)^\top d_k \geq \sigma \nabla f(x_k)^\top d_k \\ 或写成：\varphi'(\alpha) \geq \sigma \varphi'(0) \end{aligned} \]

几何意义：对斜率提要求，在可接受点处切线的斜率 \(\varphi'(\alpha)\) 不小于初始斜率的 \(\sigma\) 倍（注意初始斜率小于0）。由下图知：

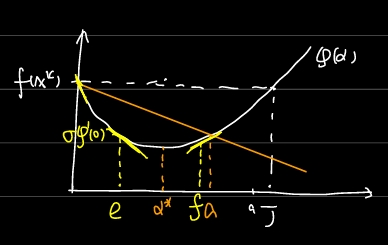
满足第一个条件的 \(\alpha\) 构成区间 \((0, a]\)，满足第二个条件的 \(\alpha\) 构成区间 \([e, J]\)，因此两个条件构成的约束为 \(\alpha \in [e, a]\)。

强 Wolfe-Powell 准则

第二个条件改为：

\[\begin{aligned} | \nabla f(x_k + \alpha_k d_k)^\top d_k | \geq | \sigma \nabla f(x_k)^\top d_k | \\ 或写成：| \varphi'(\alpha) | \geq | \sigma \varphi'(0) | \end{aligned} \]

由上图可知，满足第一个条件的 \(\alpha\) 构成区间 \((0, a]\)，满足第二个条件的 \(\alpha\) 构成区间 \([e, f]\)，因此两个条件构成的约束为 \(\alpha \in [e, \min(a,f)]\)。