雷达气象学(10)——双偏振雷达及其变量
中国气象局探测中心雷达中心有小编爆料,将于今年(2024)年底推出升级后的天气雷达拼图系统V3.1,届时就可以访问中国天气网等官方网站,查询天气雷达的双偏振量了。趁这个机会赶快了解一下双偏振雷达是个什么玩意吧!
10.1 双偏振雷达的优势
回顾本系列的开篇文章《雷达电磁波的散射》就知道,电磁波是横波,我们把电场振动所在平面称为偏振通道。常规天气雷达通过发射水平或垂直偏振通道来探测降水粒子,因此在探测过程中仅对粒子单一方向上的特性比较敏感。
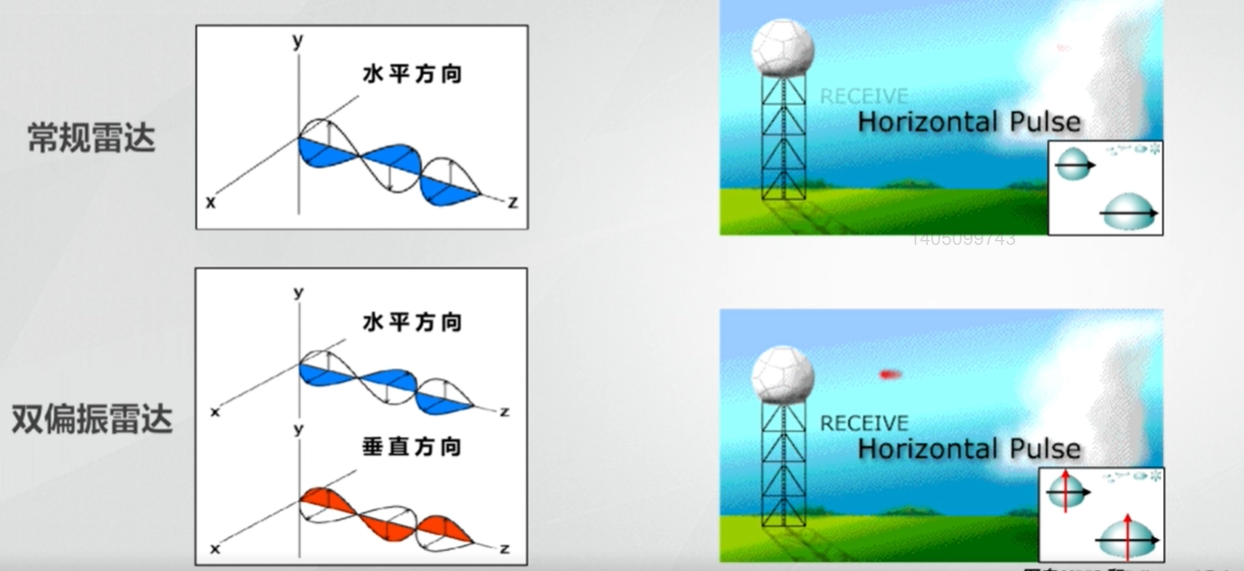
上图第一张子图中,常规天气雷达所发射的电磁波方向为水平方向,因此雷达探测的降水粒子特性更多地与降水粒子的水平方向上的特性有关。然而,在许多情况下,降水粒子在水平方向上的特性与垂直方向上存在一定的差异。为了能更准确地探测到降水粒子的结构,在常规天气雷达的基础上新增了另一个偏振通道(如上图第二张子图所示),可用于同时探测降水粒子的两个方向上的特性。这样,相比常规天气雷达,双偏振雷达能获得更多关于降水粒子特性的变量。
双偏振雷达有两种观测模式:
- 交替发射和接收模式:脉间交替发射水平和垂直偏振波,同时接收水平和垂直偏振波。这种模式比较常用。
- 同时发射和接收模式:同时发射水平和垂直偏振波,同时接收水平和垂直偏振波。这种模式对硬件的要求较高。
10.2 双偏振变量——反映降水粒子特性的变量
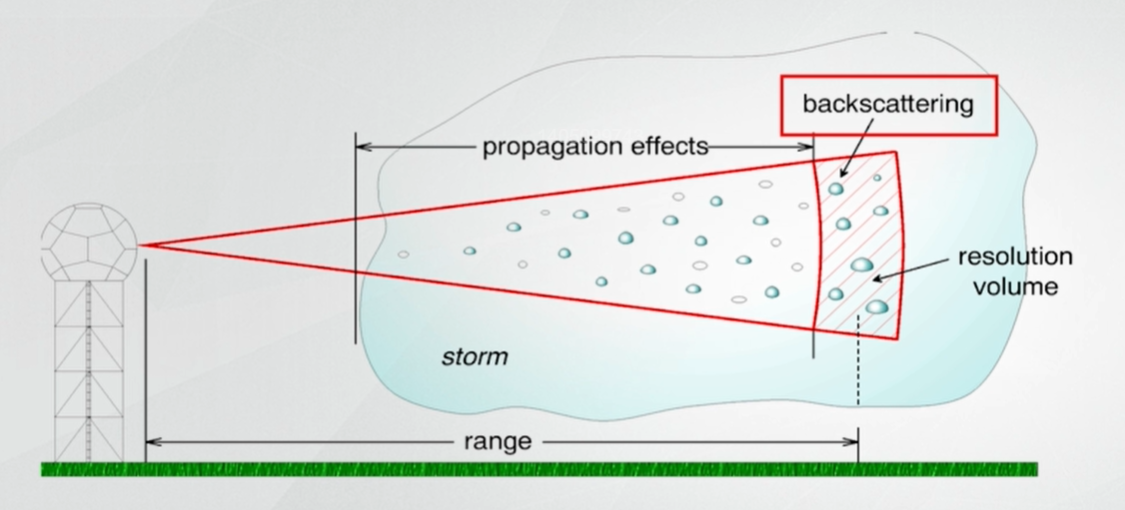
双偏振雷达发射电磁波时,目标取样体积内的水凝物粒子会对电磁波进行后向散射;与此同时,电磁波在探测到目标物之前,也会在降水介质中传播,传播过程中降水粒子会对电磁波产生作用,称为传播效应。
双偏振雷达中,与目标区域直接相关的变量有:
- 反射率因子 \(Z_H\):可以由雷达直接测量
- 差分反射率 \(Z_{DR}\):可以由雷达直接测量
- 后向散射相位 \(\delta_{hv}\)
- 协相关系数 \(\rho_{hv}\)(CC):可以由雷达直接测量
与传播效应相关的变量有:
- 差分相位移 \(\phi_{DP}\):可以由雷达直接测量
- 比差分相移 \(K_{DP}\):可间接测量
- 衰减 \(A_H\):可间接测量
- 差分衰减 \(A_{DP}\):可间接测量
- 退极化比 LDR
这些变量有什么用呢?如下表所示:
| 双偏振变量 | 用途 |
|---|---|
| 差分反射率 \(Z_{DR}\) | 判断降水粒子大小 |
| 协相关系数 \(\rho_{hv}\)(CC) | 区分降水与非降水,并识别降水相态 |
| 比差分相移 \(K_{DP}\) | 判断雨滴数目 |
下面介绍几个比较重要的双偏振变量。
10.3 差分反射率 \(Z_{DR}\)
10.3.1 差分反射率的定义
之前在《雷达电磁波的散射》讲过,对于球形粒子,若满足瑞利散射的条件下,反射率因子为:
式中,\(\lambda\) 为电磁波波长,\(K = \frac{m^2 - 1}{m^2 + 2}\),\(m\) 为粒子的复折射系数,\(\sigma\) 为降水粒子的后向散射截面。
但是,对于椭球形粒子,反射率因子并不简单:
这个 \(\sigma_{hv}\) 实际上与水凝物的形状、分布、电磁参数有关,由上式可知:
- 当水凝物的水平尺寸大于垂直尺寸时,有 \(\sigma_h > \sigma_v\),所以有 \(Z_h > Z_v\);
- 当水凝物的水平尺寸小于垂直尺寸时,有 \(\sigma_h < \sigma_v\),所以有 \(Z_h < Z_v\)。
因此,水平通道的反射率因子与垂直通道的反射率因子并不相等。为了反映两者之间的差距,使用水平反射率因子与垂直反射率因子之比,即差分反射率 \(Z_{dr}\) 来表示:
跟反射率因子一样,差分反射率也是使用分贝(dB)作为单位(使用分贝作单位时,下标一律使用大写字母),即:
降水粒子的形状和取向、粒子的介电常数是影响差分反射率的两个关键因素。首先是降水粒子的形状和取向,具体来说:

- \(Z_{DR} > 0 \mathrm{dB}\):水平椭球形粒子;
- \(Z_{DR} = 0 \mathrm{dB}\):球形粒子;
- \(Z_{DR} < 0 \mathrm{dB}\):垂直椭球形粒子。
而当粒子的介电常数减小时,差分反射率也会随之减小。现在我们来简单介绍不同水凝物(降水粒子)的差分反射率。
10.3.2 雨滴的差分反射率

雨滴的形状一般呈扁球体(水平椭球形粒子),其形状与大小密切相关。如上图左边所示为雨滴轴长比与雨滴直径的关系,由此可以发现,雨滴越大,形状就越扁,\(Z_{DR}\) 越大,且大于 0dB。

在实际的降水观测中,大雨滴和小雨滴一般是并存的,因此 \(Z_{DR}\) 会受到大雨滴数量和小雨滴数量比例的影响,另外雨滴的数量和分布也会影响 \(Z_{DR}\)。通常而言,强降雨伴随着数量较多的大雨滴,而对于弱降水来说,小雨滴占多数。
如果我们把影响 \(Z_{DR}\) 的因素综合起来,便引出了雨滴谱的概念:单位体积中雨滴的数量(或数密度)随雨滴直径的变化关系称为雨滴谱,它是雨滴生成、下落、增长、破碎、蒸发等过程的综合结果。正是不同的雨滴谱分布导致了不同的 \(Z_{DR}\)。
下面我们具体说说为什么双偏振雷达能识别不同的雨滴谱。不妨考虑两个不同的雨滴谱:
| 雨滴谱 | 1 | 2 |
|---|---|---|
| 雨滴直径 | 1mm | 3mm |
| 雨滴数量 | 729 | 1 |
| 雨强 | 5.588mm/h | 0.508mm/h |
由反射率因子的计算公式 \(Z=\sum_{i=1}^{N} D_i^6\) 可知,两者的反射率均为 29dBZ。相同的反射率意味着什么?意味着对于传统天气雷达(即单偏振的天气雷达),这两种不同的雨滴谱探测出来的结果是一样的,我们无法分辨它们的区别,尽管两者的雨强相差甚远,而双偏振雷达却能够区分两者的差别,这就是传统天气雷达所不能触及的优势了。
10.3.3 冰、雪和冰雹的差分反射率
对于冰,在下落过程中,因受到空气阻力作用,其等效形状依然是扁的,因此 \(Z_{DR} > 0 \mathrm{dB}\)。不过由于冰晶本身的尺寸较小,差分反射率也是比较小的。
对于干雪,在下落过程中,它的等效形状依然是扁的,但是其结构松散,可看做冰和空气所组成的粒子,因此介电常数较小,\(Z_{DR}\) 也较小,一般接近于 0dB。
对于湿雪,可以将其看做水、冰和空气三者的混合体。融化一部分的湿雪,其粒子形状接近于干雪,湿雪融化越多,介电常数就越大,且接近于水得介电常数,因此反射率因子和 \(Z_{DR}\) 都会增大,但是 \(Z_{DR} > 0 \mathrm{dB}\)。
对于冰雹,由于在下落过程中会不断地翻滚,其形状也会慢慢靠近球形,其 \(Z_{DR}\) 会接近于 0dB。
下面给出几个例子。第一个例子是南京信息工程大学 C 波段双偏振雷达的低仰角观测:
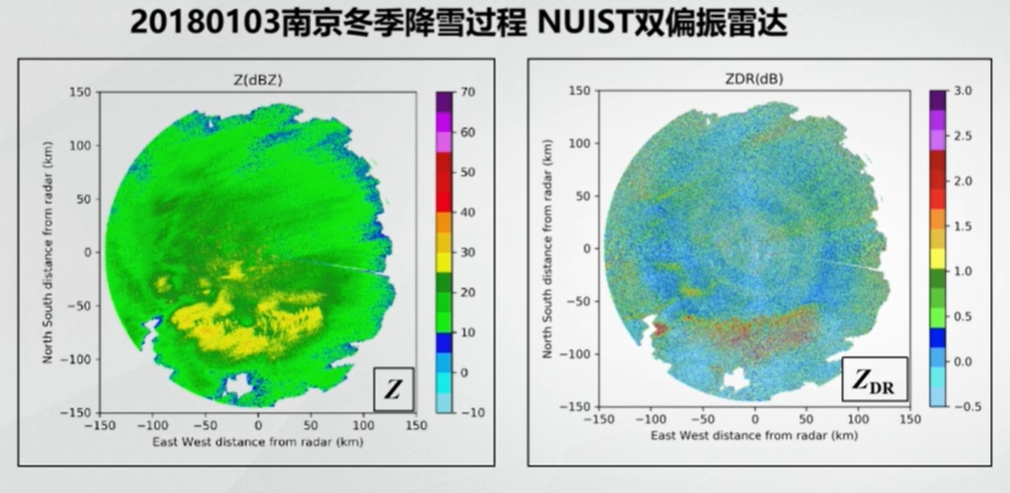
这次降水的类型为层云降水,可以看到左图的反射率因子普遍较弱,主要对应的降水粒子为雪。从右边的 \(Z_{DR}\) 图可知,其值接近于 0dB,而下面有一块区域的 \(Z_{DR}\) 相对较大,可初步说明这片区域的雪处于融化状态,因为湿雪会使 \(Z_{DR}\) 增大。
第二个例子是南京信息工程大学 C 波段双偏振雷达的高仰角观测:
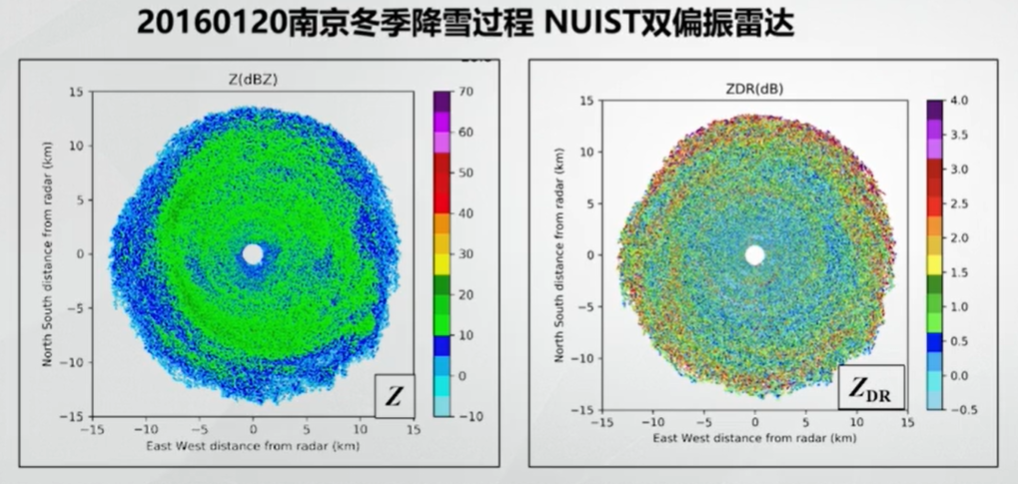
大气高空中主要为冰晶粒子,由右边的 \(Z_{DR}\) 图可知,这些冰晶粒子的形状各异,对应不同的 \(Z_{DR}\),且最大有 3dB 左右。随着下落过程的持续,聚合作用使得冰晶形成雪,粒子形状逐渐变为球形,\(Z_{DR}\) 将变小。
第三个例子是广州 S 波段双偏振雷达的观测:
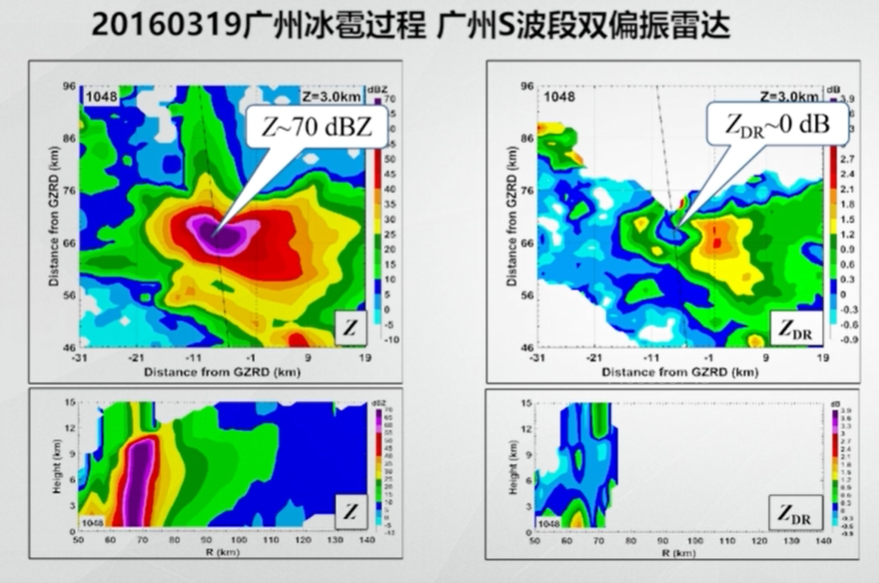
左上图为 PPI 反射率因子图,可看到最大回波强度有 70dBZ,而且还能看到三体散射回波 TBSS 位于回波核心区的后侧,其沿着雷达径向方向延伸,说明存在着冰雹天气。而在右上的 PPI-\(Z_{DR}\) 图可以看到,回波核心区即冰雹区的 \(Z_{DR}\) 接近 0dB,而冰雹区周围的降水区则大于 0dB。
同样的特征发生在 RHI 上,右下图为 RHI 反射率因子图,冰雹区延伸到 8km 高度;而在右下的 RHI-\(Z_{DR}\) 图中,对应区域的 \(Z_{DR}\) 接近 0dB。
上述这几个例子提醒我们,不是有了双偏振雷达就高枕无忧了,很多时候也要参考单通道雷达的探测,要两只手一起抓才能准确判断降水类型。
10.3.4 层云降水的差分反射率
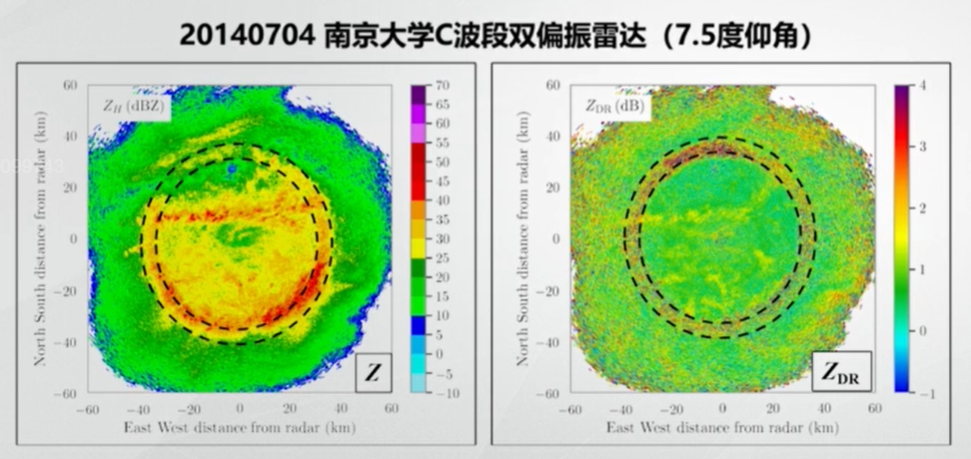
在这个例子中,两张图均为 PPI,左边的反射率因子图和右边的 \(Z_{DR}\) 图均出现了零度层亮环。关于零度层亮带的详细介绍已于本系列的《反射率因子图分析(气象回波篇)》讲过,现在来分析为什么在 \(Z_{DR}\) 图上会出现这样的零度层亮带:
- 降水粒子在 0˚C 层以上:较大的降水粒子大多为冰晶和雪花,所以在右图的亮环以外 \(Z_{DR}\) 较弱;
- 降水粒子在 0℃ 层附近:此时降水粒子刚发生融化,其表面出现一层水膜。同时,冰晶和雪花在下降过程中,有强烈的碰并聚合作用,导致粒子逐渐变成球形,介电常数增大,所以 \(Z_{DR}\) 也随之增大,在图中呈现一个亮环;
- 降水粒子在 0˚C 层往下:当冰晶和雪花继续下降至完全融化为水滴时,\(Z_{DR}\) 也随之减小。
10.3.5 对流降水的差分反射率
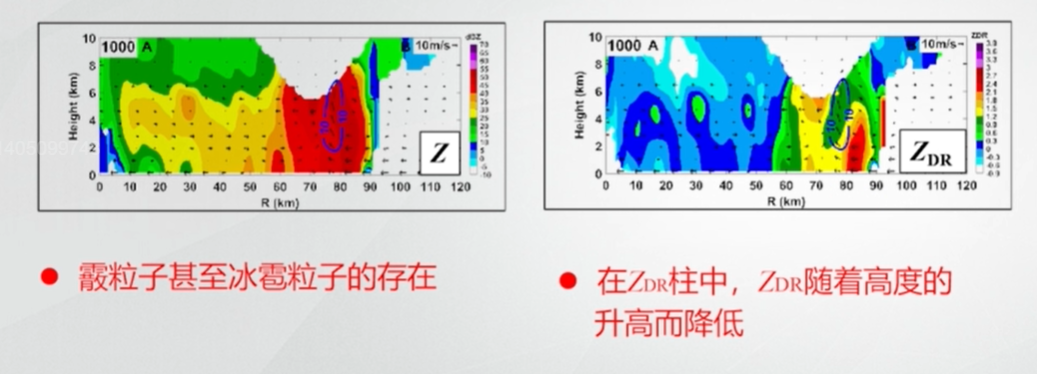
这是 2016 年 5 月 15 日广州的一次飑线过程,两张图均为 RHI。左图为反射率因子图,可发现对流高度达到 8km,强回波区突破零度层,表明可能有霰粒子或冰雹粒子。在右边 \(Z_{DR}\) 图所对应区域也有一个强 \(Z_{DR}\) 区,称为 ZDR 柱,其 \(Z_{DR}\) 值随高度增加而减小。
10.4 相关系数 \(\rho_{hv}\)
相关系数 \(\rho_{hv}\) 在雷达应用中也可写为 CC,即 Correlation Coefficient 的缩写,无单位,用于描述同时接收到的前后脉冲变化情况的 \(Z_H\) 和 \(Z_V\) 之间相关程度的物理量,一般可用于识别降水和非降水回波。下图为常见水凝物的 CC:
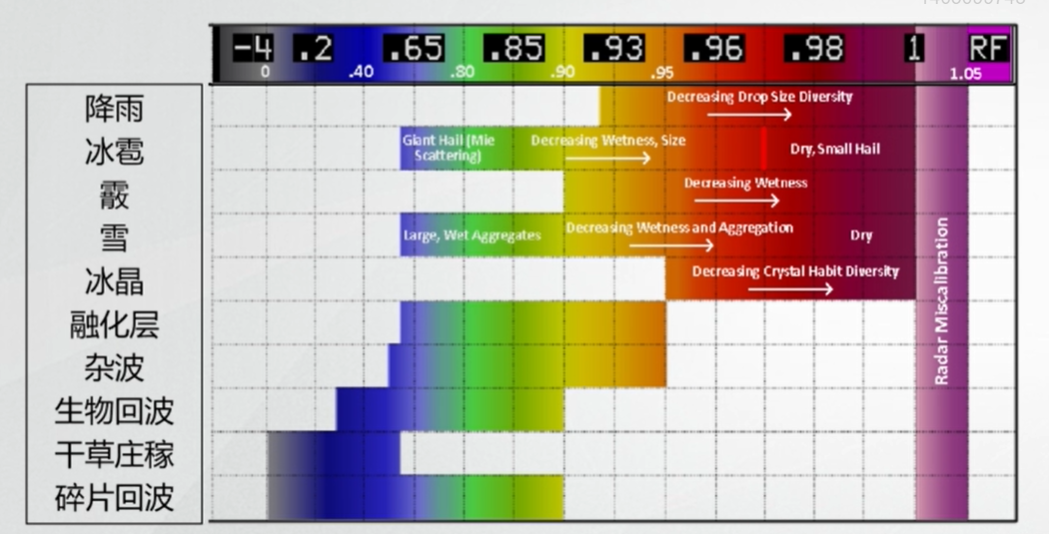
- 小雨滴的形状接近于球形,因此 CC 接近于 1;而随着雨滴的增大,其形状变为扁平,CC 也会有所降低。
- 对于冰雹和霰,当粒子较小时,CC 一般大于 0.95;当粒子开始融化时,CC 开始降低。
- 对于干雪,CC 较大且接近 1;对于湿雪,为融化中的雪,CC 降低,甚至可以低于 0.9。
- 对于杂波和地物杂波,CC 明显小于 0.8,这也是为什么 CC 能识别降水和非降水回波的缘故。
10.5 比差分相移 \(K_{DP}\)
我们知道,电磁波在真空中以光速传播,而在电介质中的传播速度会降低,因此对于同样的传播距离,真空中的电磁波的波数要比电介质中的电磁波少,或者说两者存在着相位差。同样的道理,对于非球形粒子,水平偏振波和垂直偏振波的传播速度是不同的,所以随着传播距离的增加,两者的波数也会存在差异,或者说两者存在着相位差,这个相位差就称为差分相移 \(\phi_{DP}\),如下图所示。
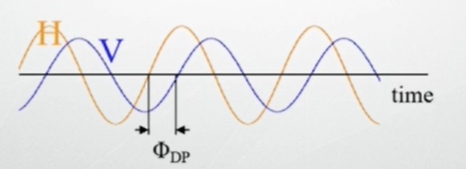
\(\phi_{DP}\) 对较大尺寸水滴非常敏感,而且粒子数量越多,它的数值变化越快,但它是累积效应的参数,即随距离的增加而线性增加,其数值在不同位置、不同时刻不能直接对比使用。于是引入了一个新的参数:比差分相移。
在单位距离上,由电介质所导致的水平通道和垂直通道的相位差,就称为比差分相移 \(K_{DP}\),单位为度/km,其物理意义是单位距离上降水介质对 \(\phi_{DP}\) 的贡献,其计算公式如下:
下图为 S 波段各种水凝物粒子的 \(K_{DP}\) 值:
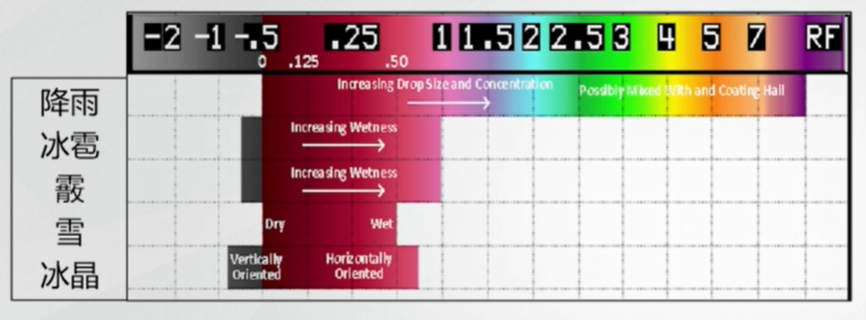
- 降雨随着粒子的直径和浓度增大,\(K_{DP}\) 逐渐增大。
- 对于同样的雨滴谱分布,电磁波波长越短,\(K_{DP}\) 越大。
- 对于冰雹、霰、雪,\(K_{DP}\) 较小且接近于 0;但是当它们开始融化时,由于粒子外部包裹着一层水膜,\(K_{DP}\) 显著增大。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号