雷达气象学(5)——多普勒天气雷达的原理
5.1 多普勒效应和多普勒频移
你是否遇到过这样的情景?一辆救护车不断尖叫着向你驶来,此时笛声非常刺耳;当救护车从你身旁经过后,笛声没有之前那么刺耳了,响度逐渐减弱,直到声音消失。

为什么会出现这样的现象?首先说明,声音也是一种波,称为声波。如上图所示,当你在运动的声波的前方时,声波被压缩,波长变得较短,从而频率变高,声音听起来就刺耳;当你在运动的声波的后方时,声波被拉长,波长变得较大,从而频率变低,声音听起来低沉。这种现象被称为多普勒效应。声波的运动速度越大,这种效应就越强。
现在正式给出多普勒效应的定义:多普勒效应是指发射的电磁波(频率为 \(f\))被远处运动的目标物体(速度为 \(v\) )反射回来,接收到的电磁波发生频移(频率为 \(f_d\) )的现象。由相对运动造成的频率变化称为多普勒频移,频移量称作多普勒频率 \(f_d\)。如果把本节开头的“你”换成雷达,把“救护车”换成待测风,那么这样的雷达就是多普勒雷达,这就是雷达测风的基本原理。
但是,多普勒雷达并不能直接测得目标的真实风速,而是径向风速。什么是径向速度?如果学过高中物理,就知道速度是一个向量,根据平行四边形法则可以分解为两个速度分量。以本节开头为例子,如下图所示:
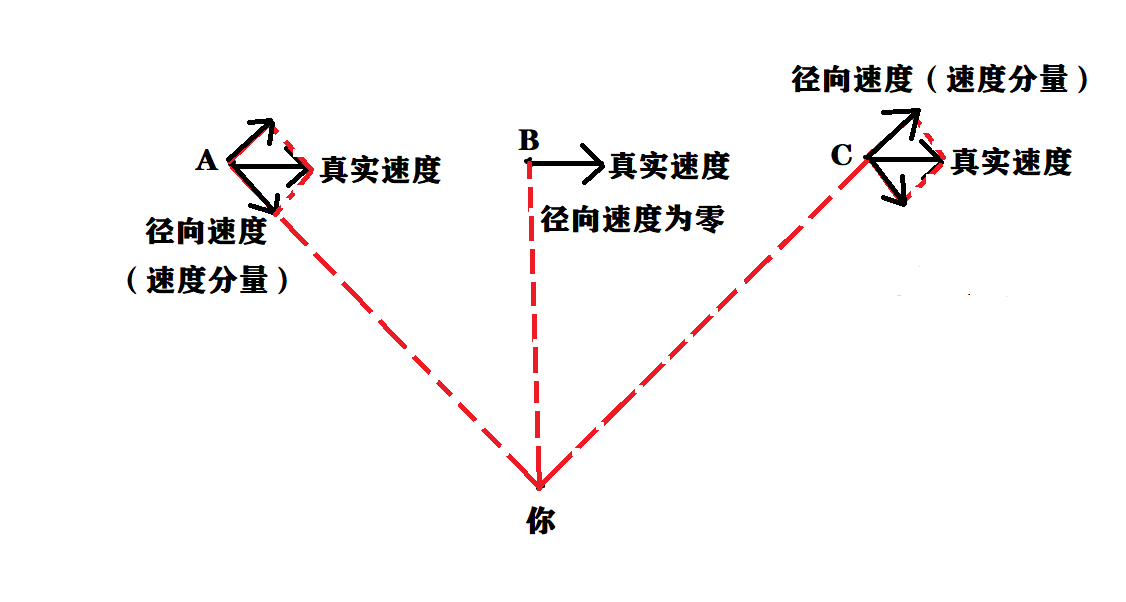
- A 点:救护车向你驶来时,其速度可以分解为朝向你的分量(径向速度)和另一个分量;
- B 点:救护车刚好行驶到你面前,其速度无法沿着你的方向进行分解,因为你正对救护车的方向与实际速度的方向刚好垂直,径向速度为零;
- C 点:救护车远离你驶去时,其速度可以分解为背向你的分量(径向速度)和另一个分量。
实际上径向速度就是真实速度的一个分量。如果忘记什么是平行四边形法则的同学,可以回去翻翻课本哟。
现在来推导这个频移量 \(f_d\)。若假定径向风速为 \(v_r\) ,多普勒雷达频率为 \(f\),目标与雷达的距离为 \(r\),则往返一次的距离为 \(2r\)。这个距离可以用波长来衡量,即 \(\frac{2r}{\lambda}\) 个波长,用弧度制表示即为 \(\frac{4 \pi r}{\lambda}\) 个弧度。若发射电磁波在天线处的相位为 \(\phi_0\),那么电磁波被散射回天线时的相位为:
其相位随时间的变化率为(即角速度 \(\omega\)):
一般规定物体趋近雷达时的径向速度 \(v_r\) 为正,远离雷达时的径向速度 \(v_r\) 为负。根据径向速度的定义,径向速度为矢径长度 \(r\) 随时间的变化率:
把上面两式结合即可得到:
又因为 \(\omega = 2 \pi f_d\),代入上式整理得:
从上式可以看出,频移量(即多普勒频率)\(f_d\) 与径向速度和波长有关。以上就是雷达测速的理论依据了。
5.2 最大不模糊速度和速度模糊
5.2.1 脉冲对处理技术
由上一节内容可知,我们可以通过测量频移的方法来得到径向速度。但是,我国新一代雷达系统即 CINRAD 并不采用测量频移的方法,而是利用相继返回的两个脉冲对之间的位相的变化,这种脉冲对位相的变化可以比较容易且准确地测量。这种测速技术叫做脉冲对处理。
假设第一个雷达发射的第一个脉冲遇到目标物时,该目标物距离雷达的距离为 \(r\),则该目标物产生的雷达回波回到雷达的相位为:
一个脉冲重复周期(PRT)后,第二个脉冲发出,当第二个脉冲遇到目标物时,该目标物距离雷达的距离为 \(r+\Delta r\),则该目标物对于第二个脉冲回波到达雷达的相位为:
相继返回的两个脉冲之间的相位差为:
根据径向速度的定义式,可得到目标物沿雷达波束径向速度 \(v_r\) 的表达式为:
实际中,雷达最终给出的径向速度是从多个脉冲对得到的径向速度的平均值,称为平均径向速度。
5.2.2 最大不模糊速度
雷达能测量的一个脉冲到下一个脉冲的最大相移上限是 \(\pi\)。与脉冲对相移 \(\pi\) 对应的目标物的径向速度值称为最大不模糊速度 \(v_{\mathrm{max}}\)。最大不模糊速度是雷达能够不模糊地测量的最大平均径向速度,其对应的相移是 \(\pm \pi\)。最大不模糊速度又称为最大径向速度。
将 \(\Delta \phi = \pi\) 代入上式,可得最大不模糊速度与脉冲重复频率 PRF 和波长的关系:
现在我们来简单介绍由多普勒天气雷达所生成的雷达产品——径向速度图。顾名思义,径向速度图就是反映雷达探测范围内的径向速度分布,它属于 PPI 显示,也就是说是(在锥面上)不同高度的径向速度。同心圆的中心位置是雷达所在位置,离雷达越远,高度越高。
如下图所示,右面的不同色阶表示不同径向速度和方向:暖色阶表示离开雷达的径向速度,冷色阶表示流向雷达的径向速度(有的速度图的色阶可能相反)。中间白色的线是零速度线,即径向速度为零。我们还可以注意到此雷达的最大模糊速度为 27m/s。
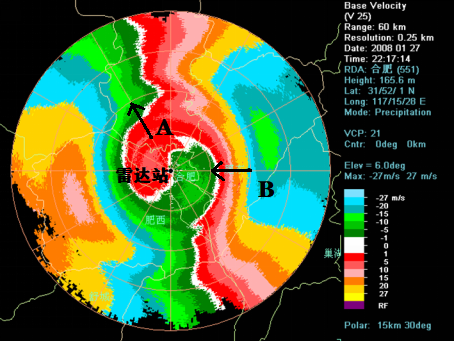
需要提醒的是,径向风速和径向风向并不代表真实风速和风向。如上图所示:
- A 点处是远离雷达的径向速度;
- B 点处是流向雷达的径向速度;
- 零速度线有两种情况:要么实际风速为零,要么雷达波束与实际风向垂直。
因此,A 点和 B 点都不是真实速度,我们现在只能得知其中一个速度分量,那么如何通过此图反求出真实风的速度和方向呢?这就是下一篇文章要介绍的了。
5.2.3 速度模糊
当实际径向速度超过最大不模糊速度限定的范围时就会出现速度模糊,简单理解就是“速度爆表”了。比如,某个雷达的最大径向速度的测定范围为 -20m/s ~ +20m/s,一旦实际径向风速超过 +20m/s,假设为 +21m/s,那么在 PPI 图像上显示的可能就变成 -20m/s 了,这就是“爆表”。
那么我们如何分辨速度模糊呢?一个很直接的想法是:大气中风场的分布总是连续的,很少出现风速“断层”的情况,这就是风速的连续性原则。如果我们发现某个地方的风速变化非常剧烈,即径向风速从正(负)极值突变为负(正)极值,那么可以判断这个地方可能出现了速度模糊。
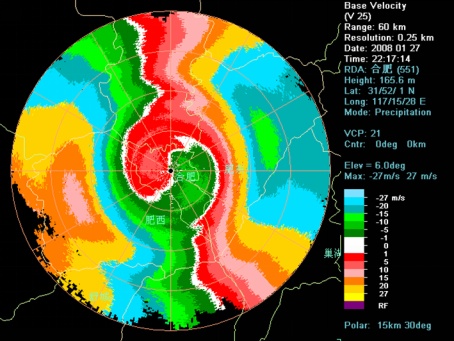
举个例子,如上图所示,零速度线呈“S”型分布,在“S”的左边和右边都有浅黄色区域和浅蓝色区域相邻,浅黄色和浅蓝色区域对应的径向风速分别为 -27m/s 和 +27m/s,风速突变,说明左右两边都发生了速度模糊。分析可发现左边和右边的径向速度分别为 -54m/s 和 +54m/s。
但是,雷达是不知道风速“爆表”的,那么雷达是如何分辨是否发生了速度模糊的呢?这就是速度退模糊算法。
5.2.4 速度退模糊算法
速度退模糊算法的本质是:根据连续性原则,将每个速度初猜值与它的周围的相邻速度值相比较,如果一个速度初猜值与它的周围值显著不同,则该算法试图用另一个可能的值替换那个速度初猜值。
WSR-88D 的第一猜速度 \(v_{\mathrm{first}}\) 以假设脉冲对相移小于 \(\pi\) 为基础:如果运动目标的脉冲对真实相位差小于 \(\pi\),那么雷达对径向速度的初猜值 \(v_{\mathrm{first}}\) 是正确的,即观测是不模糊的;如果运动目标的脉冲对真实相位差超过 \(\pi\),那么雷达对径向速度的初猜值 \(v_{\mathrm{first}}\) 是不正确的,或者说速度是模糊的。最后,雷达根据模糊速度的初猜值 \(v_{\mathrm{first}}\) 和最大不模糊速度\(v_{\mathrm{max}}\) 得到一系列可能的速度值:
式中 \(n\) 为速度折叠次数。
速度退模糊算法的大致步骤如下:
- 径向连续性检查
- 九点平均
- 扩展搜索
- 环境风表
由于篇幅有限,此处就不展开了。这些步骤旨在通过比较和修正速度初猜值,以减少或消除由于各种因素(如高切变和孤立回波情况)导致的速度模糊问题。
5.3 最大不模糊距离和距离折叠
5.3.1 最大不模糊距离
最大不模糊距离是指:当雷达发出一个脉冲遇到距离 \(r\) 处的目标物产生的后向散射波返回雷达时,下一个雷达脉冲刚好发出。这个距离 \(r\) 称为最大不模糊距离 \(r_{\mathrm{max}}\)。雷达传播至 \(r_{\mathrm{max}}\) 后的回波返回雷达的时间,恰好是两个脉冲之间的时间间隔,即脉冲重复周期 PRT。计算公式如下:
式中,\(c\) 为光速,PRF 为脉冲重复频率。
5.3.2 距离折叠
距离折叠(距离模糊)是指雷达确定的目标物方位是正确的,但距离却是错误(模糊)的。当目标物位于最大不模糊距离 \(r_{\mathrm{max}}\) 之外时,雷达却把目标物显示在 \(r_{\mathrm{max}}\) 以内的某个位置,因此称为距离折叠。
距离折叠是如何发生的呢?我们首先考虑没有发生距离折叠的情况。如下图所示,该雷达的最大不模糊距离 \(r_{\mathrm{max}} = 230\mathrm{km}\)。
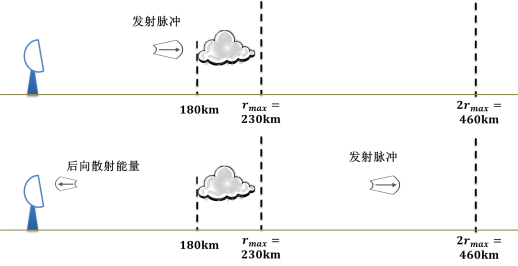
现假设有一个目标物位于 180km 处,当雷达发射的脉冲到达该目标物时,脉冲的大部分能量继续向前传播,而少量能量被目标物后向散射回雷达。当这些后向散射波到达雷达时,脉冲的大部分能量已经传播到距离雷达 360km 的位置。此时第二个脉冲还没有发射,雷达准确的把目标定位在 180km 处,目标物的定位不存在模糊问题。
再来考虑发生了距离折叠的情况。如下图所示,该雷达的最大不模糊距离也是 \(r_{\mathrm{max}} = 230\mathrm{km}\)。
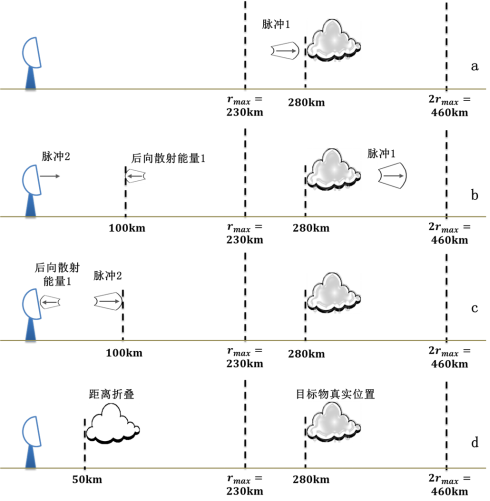
现在来解释每张子图到底发生了什么:
- 图 a:有一个目标物位于 280km 处,即位于最大不模糊距离之外,雷达向该目标物发射脉冲 1。
- 图 b:当雷达发射的脉冲 1 到达该目标物时,脉冲 1 的大部分能量继续向前传播,而少量能量被目标物后向散射回雷达。当脉冲 1 的后向散射能量到达距雷达 100km 时,脉冲 2 发射。此时,雷达认为接下来返回雷达的能量均来自脉冲 2。
- 图 c:当脉冲 2 传播到 100km 时,脉冲 1 的后向散射能量正好到达雷达。
- 图 d:此时,雷达认为接收到的能量来自脉冲 2,且往返总共 100km,则认为在 50km 处遇到目标物,而不是脉冲 1 在 280km 所遇到的目标物。
如果雷达的最大不模糊距离为 \(r_{\mathrm{max}}\),则称位于 \(0 \sim r_{\mathrm{max}}\) 的目标物处于第一程,位于 \(r_{\mathrm{max}} \sim 2 r_{\mathrm{max}}\) 的目标物处于第二程,位于 \(2r_{\mathrm{max}} \sim 3 r_{\mathrm{max}}\) 的目标物处于第三程,以此类推。第二程以上的回波称为多程回波。
5.3.3 距离去折叠的方法
如何解决距离折叠?以下有几种方法:
- 用随机相位编码技术消除距离折叠。
- 调节脉冲重复频率 PRF,这样便可以改变 \(r_{\mathrm{max}}\),并可能在所关心的区域将距离折叠退掉。
- 选择一个较高的仰角扫描能克服距离折叠问题。
- 采取变换探测地点的方式可以观察到同一个风暴的不同侧面。
另外,有一种距离去折叠的算法,因为比较复杂,篇幅有限,此处就不展开了。
5.4 多普勒两难
最大不模糊速度 \(v_{\mathrm{max}}\) 和最大不模糊距离 \(r_{\mathrm{max}}\) 都是与脉冲重复频率 PRF 相关的,如果查看这两者的乘积,会发现 PRF 正好可以上下约去,即:
上式说明,对每个特定雷达而言,在确定的频率下,探测的最大距离和最大速度不能同时达到最大值,这就是多普勒两难。对于多普勒两难的处理,美国新一代天气雷达 WSR-88D 采用了提供一系列脉冲重复频率供选择,在低仰角、中等仰角和较高仰角分别采用不同的取样策略。我国新一代天气雷达中的 SA、SB 和 CB 型雷达都采用了 WSR-88D 的方案,如下表所示。
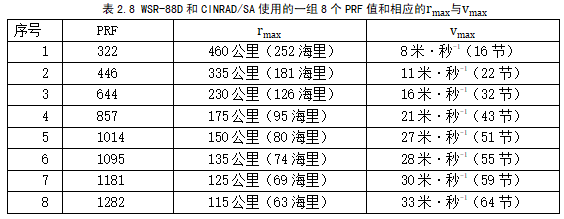
5.5 WSR-88D 的取样技术
(有空再写)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号