G
N
I
D
A
O
L

大气热力学（13）——强对流指数之二（热力稳定性指数）

本篇文章继续上篇的内容，介绍了根据预报员多年经验总结的各种强对流预报指数，希望这部分内容能对你有所帮助。

目录

13.1 沙氏指数（Showalter Index, SI）

沙氏指数的定义：850hPa 上的湿空气沿着干绝热线上升，到达凝结高度后再沿着湿绝热线上升至 500hPa 具有的气块温度（\(T_{i500}\)）与 500hPa 环境温度（\(T_{e500}\)）之差。单位为 ℃，计算公式如下：

\[\mathrm{SI} = T_{e500} - T_{i500} \]

SI < 0 表示层结不稳定，SI 负值越大，就越不稳定。

SI 的示意图如下：

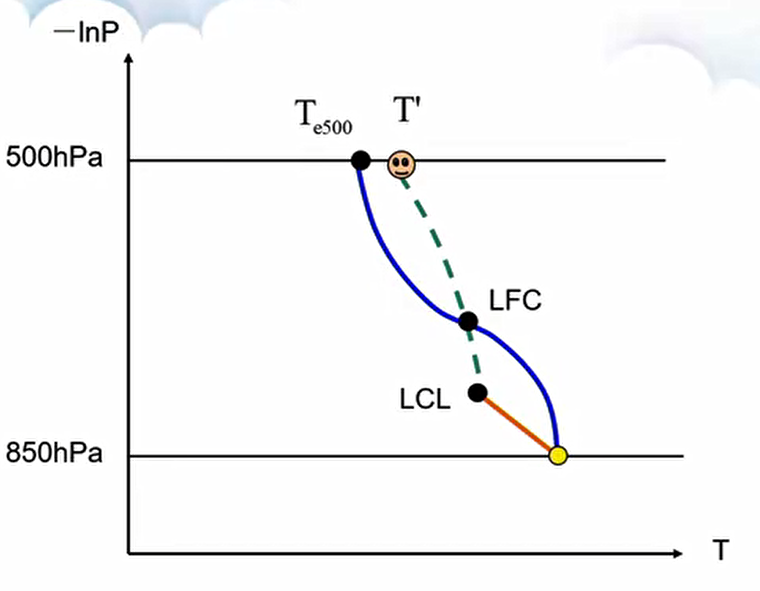
image

在这张 T-lnP 图中，蓝色曲线为层结曲线（温度廓线），橙色曲线和绿色曲线组成了气块的状态曲线，\(T'\) 即为本文所述的 \(T_{i500}\)。由该图可以很容易得知影响 SI 的几个因素：

  • 当状态曲线不变时，环境温度直减率越大，温度廓线就越往左移动，SI 的负值就越大，层结越不稳定。
  • 当环境温度直减率（即温度廓线）不变时，状态曲线越偏右，SI 的负值就越小，层结越稳定。

根据国外的资料，SI 与对流性天气的关系如下表所示：

SI 对流程度
SI>3 发生雷暴的可能性很小或没有
0<SI<3 有发生阵雨的可能
-3<SI<0 有发生雷暴的可能
-6<SI<-3 有发生强雷暴的可能
SI<-6 有发生严重对流天气的可能

使用 SI 时需要注意几个点：

  • 起始高度为 850hPa，上层高度为 500hPa；
  • 对于海拔较高的地区，不能直接用 SI 指数，而是应该在低层、高层分别取两个等压面代替 850hPa 和 500hPa；
  • 如果 850hPa 和 500hPa 之间存在锋面或者逆温层，SI 无意义；
  • 阈值（如上表）必须针对不同季节、根据各地实际情况确定。

13.2 抬升指数（Lifted Index, LI）

抬升指数的定义：根据修正后（一般是近地面 900m 高度或 1.5km 高度）的露点和温度，气块自地面沿着干绝热线上升，到达凝结高度后再沿着湿绝热线上升至 500hPa 具有的气块温度（\(T_{i500}\)）与 500hPa 环境温度（\(T_{e500}\)）之差。LI 的定义与 SI 很像，区别仅为抬升高度的不同。单位为 ℃，计算公式如下：

\[\mathrm{LI} = T_{e500} - T_{i500} \]

LI < 0 表示层结不稳定，LI 负值越大，就越不稳定。

修正方法如下图所示：

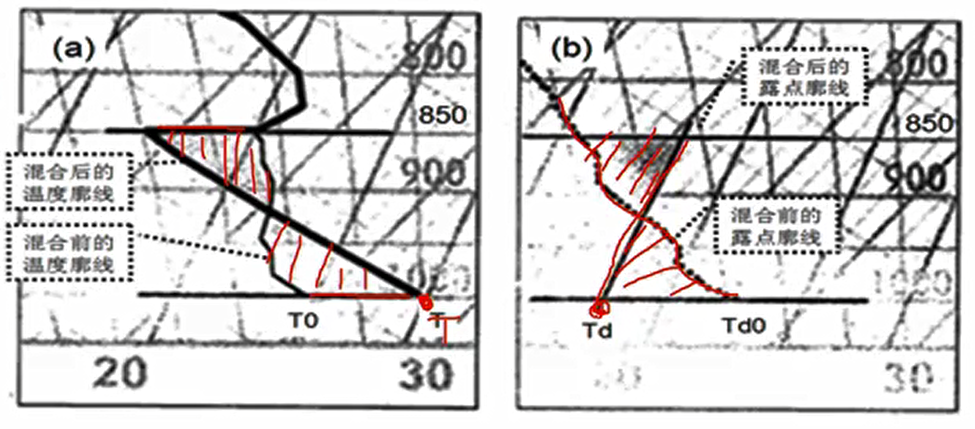
image

图中，\(T_0\) 和 \(T_{d0}\) 为混合前气块的温度和露点。这里假定地面气块所在高度为 1000hPa，选取混合层的厚度为 150hPa，即修正范围为 1000hPa ~ 850hPa。

  • 地面温度 \(T\) 的修正：气块经过深层混合后，低层的温度廓线调整为左图所示的干绝热线，在图上满足原温度廓线和新温度廓线相交、与 850hPa 和 1000hPa 围成的两个闭合图形面积（即左图两个红色阴影面积）相等。850hPa 以上的温度廓线不变。这样，干绝热线与地面的交点为混合后的地面温度 \(T\)。
  • 露点温度 \(T_d\) 的修正：混合后的地面露点及地面以上 150hPa 的露点廓线（露点曲线）类似地面温度的求法，只不过用到了等饱和比湿线而不是干绝热线，要求在图上满足原露点廓线和新露点廓线相交、与 850hPa 和 1000hPa 围成的两个闭合图形面积（即右图两个红色阴影面积）相等。这样，露点廓线与地面的交点为混合后的露点温度 \(T_d\)。

下图是一个例子。红色实线为温度廓线，绿色实线为露点廓线，黄线为状态曲线。

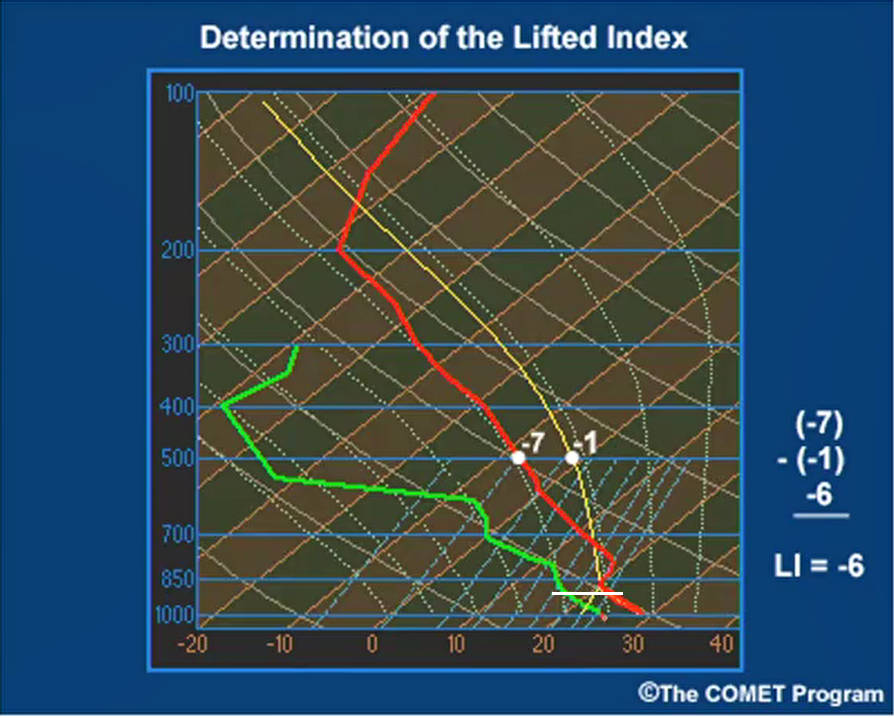
image

该图作了如下修正：

  • 选取的修正范围为 1000hPa ~ 900hPa（白色等压线处）。
  • 地面温度 \(T\) 的修正：由于温度廓线和状态曲线接近，因此不需要进行修正。
  • 露点温度 \(T_d\) 的修正：修正前的露点温度为露点廓线与 1000hPa 等压线的交点处，使用一条等饱和比湿线（图中低层的黄色细实线）划分得到两个相等面积，该等饱和比湿线与1000hPa 等压线的交点处即为修正后的露点温度 \(T_d\)。可以看到修正后的露点变小了。

接下来计算 LI：

  • 从修正的露点温度沿着该等饱和比湿线（图中低层的黄色细实线）、与从修正的地面温度沿着干绝热线（注意，该线不一定与状态曲线重合，这个例子只是巧合！），两者相交的点所在高度即为抬升凝结高度。
  • 接着，气块从该抬升凝结高度沿着湿绝热线（再次注意，该线不一定与状态曲线重合，这个例子只是巧合！）到达 500hPa，得到 \(T_{i500} = -1\)。
  • 温度廓线与 500hPa 相交处读出温度为 \(T_{e500} = -7\)。
  • 根据公式计算 LI = (-7) - (-1) = -6。

LI 与对流性天气的关系如下表所示：

LI 对流程度
0<LI<3 很微弱，基本不会有对流
-3<LI<-1 较弱，如果有动力触发条件也会产生强对流
-5<SI<-3 较不稳定，容易触发强对流
-8<SI<-6 很不稳定，雷暴较强
SI<-8 极不稳定，可能产生极端强对流

LI 不考虑强烈垂直风切变，或者干层的因素，因此可能会低估对流强度。

13.3 对流性稳定度指数（IC）

对流性稳定度指数的定义：上下层的假相当位温的差值。单位为 ℃，计算公式为：

\[\mathrm{IC} = \theta_{se上} - \theta_{se下} \]

IC > 0 为对流性稳定，IC < 0 为对流性不稳定。层次的选择并不唯一，如选取 \(\theta_{se500} - \theta_{se850}\) 或 \(\theta_{se700} - \theta_{se850}\) 都是可以的。

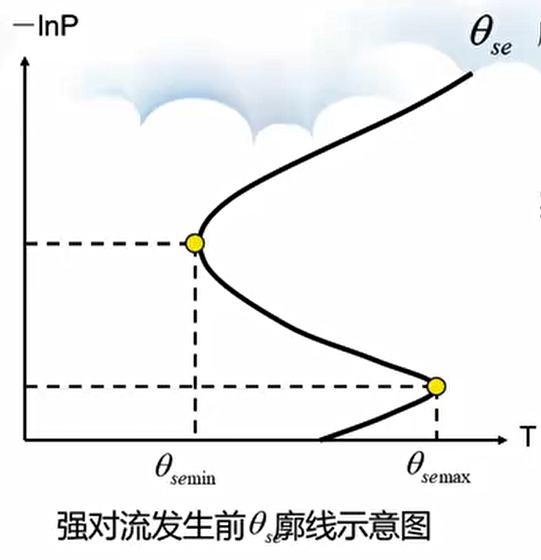
image

由于 IC 涉及的高度是固定的，数值不太客观，于是提出了最大对流性稳定度指数（BIC），如上图所示，其定义为最大假相当位温与最小假相当位温的差值，计算公式如下：

\[\mathrm{BIC} = \theta_{se\mathrm{min}} - \theta_{se\mathrm{max}} \]

在实际计算时，\(\theta_{se\mathrm{min}}\) 取高度 650~500hPa 的假相当位温最小值，\(\theta_{se\mathrm{max}}\) 取地面 ~ 1500m 的假相当位温最大值。计算 BIC 后，还要对其值进行检查，需要满足条件 \(\theta_{se\mathrm{max}} - \theta_{se\mathrm{min}} \geq \theta_{\mathrm{sec}}\)。这个 \(\theta_{\mathrm{sec}}\) 是阈值，比如取 20℃。只有达到了这个阈值条件，才去做强对流的预报工作。

13.4 K指数（K-Index）

13.4.1 K指数的定义与计算公式

K 指数的计算公式如下：

\[\mathrm{K} = (T_{850} - T_{500}) + T_{d850} - (T - T_d)_{700} \]

其中，\(T_{850} - T_{500}\) 为垂直温度直减率，\(T_{d850}\) 反映了低层水汽条件，\((T - T_d)_{700}\) 反映了低层饱和程度。K 指数就是综合反映上述三项的物理量，现在来简要说明这三个项：

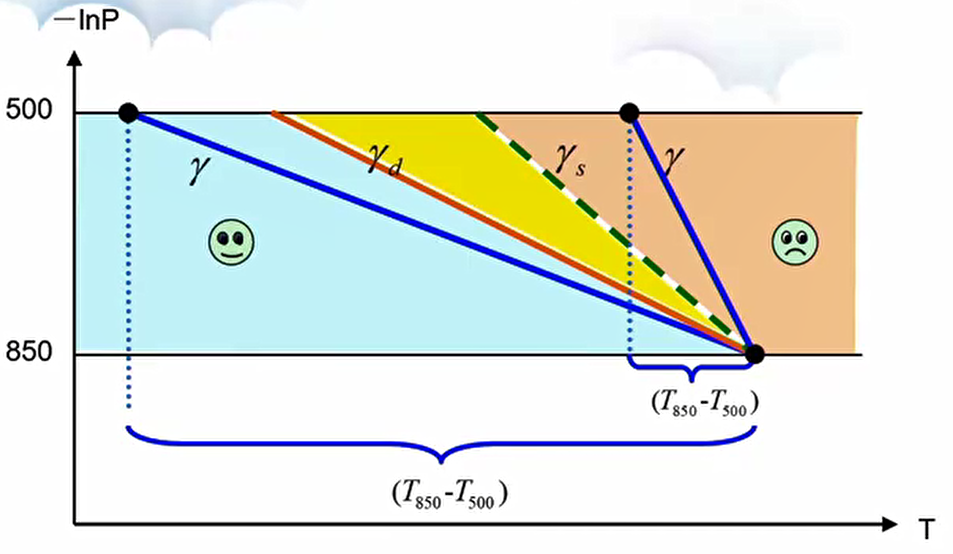
image

  • \(T_{850} - T_{500}\)：如上图所示，高层越冷、低层越暖，则该项值越大；

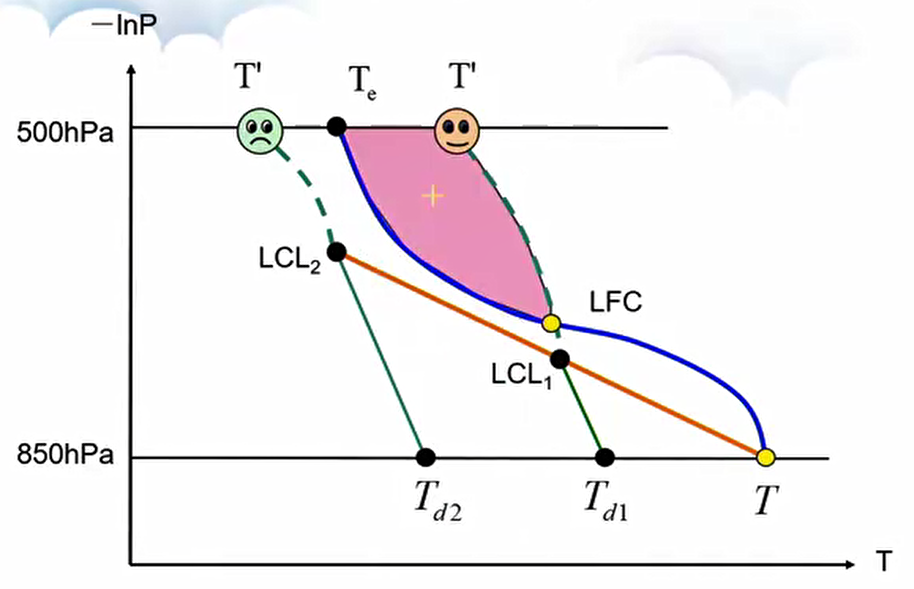
image

  • \(T_{d850}\)：如上图所示，低层湿度越大，则该项值越大；
  • 若 \((T - T_d)_{700}\) 小且 \(T_{d850}\) 大，则说明中低层湿层较厚。

K 指数与可能出现雷暴活动的关系如下表所示：

K 雷暴活动程度
K<20 无雷暴
20<K<25 孤立雷暴
25<K<30 零星雷暴
30<K<35 分散雷暴
K>35 成片雷暴

13.4.2 使用K指数预报强对流时的问题

（1） K 指数为负值，但仍有强对流天气发生，为什么？

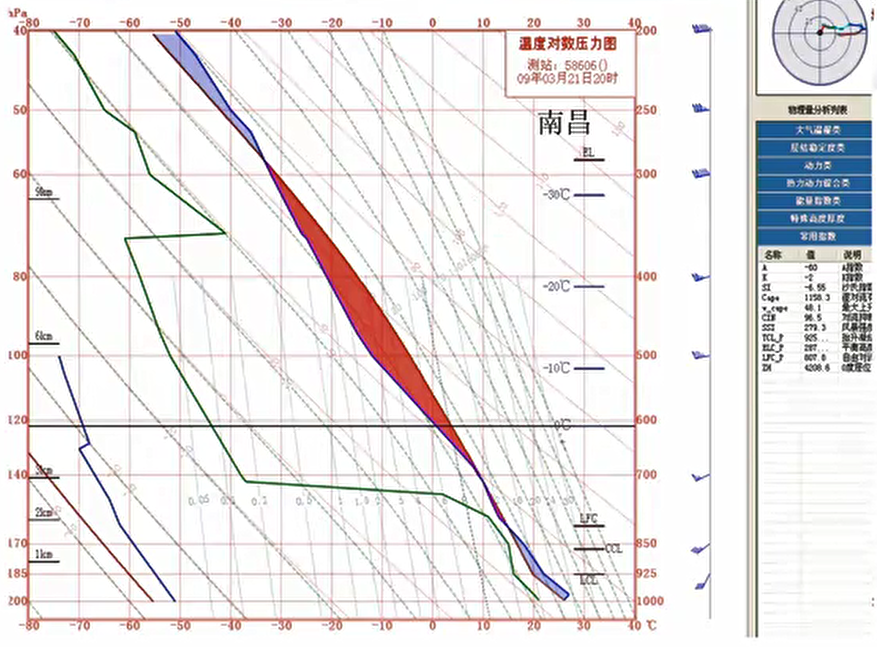
image

上图是一张 T-LnP 图，注意等温线不是斜的！从图中的层结曲线（温度廓线）可读出：

\[T_{850} = 18℃，T_{500} = -12℃，T_{700} = 9℃ \]

从图中的露点曲线可读出：

\[T_{d850} = 15℃，T_{d700} = -38℃ \]

于是根据公式可计算出 \(K=-2\)，对应上面表格认为无雷暴发生，但实际上该地当天出现了强对流天气，这是为什么呢？说明在作预报的时候，不能仅靠强对流指数来做出判断，还要根据风场、温度、湿度等特征做出调整。

从该图的露点曲线可看出，当天中高层的湿度特征为上干下湿，而且 CAPE 的面积也较大，是一个典型强对流前兆所应有的特征。

（2） K 指数相近，但强对流现象不相同，为什么？

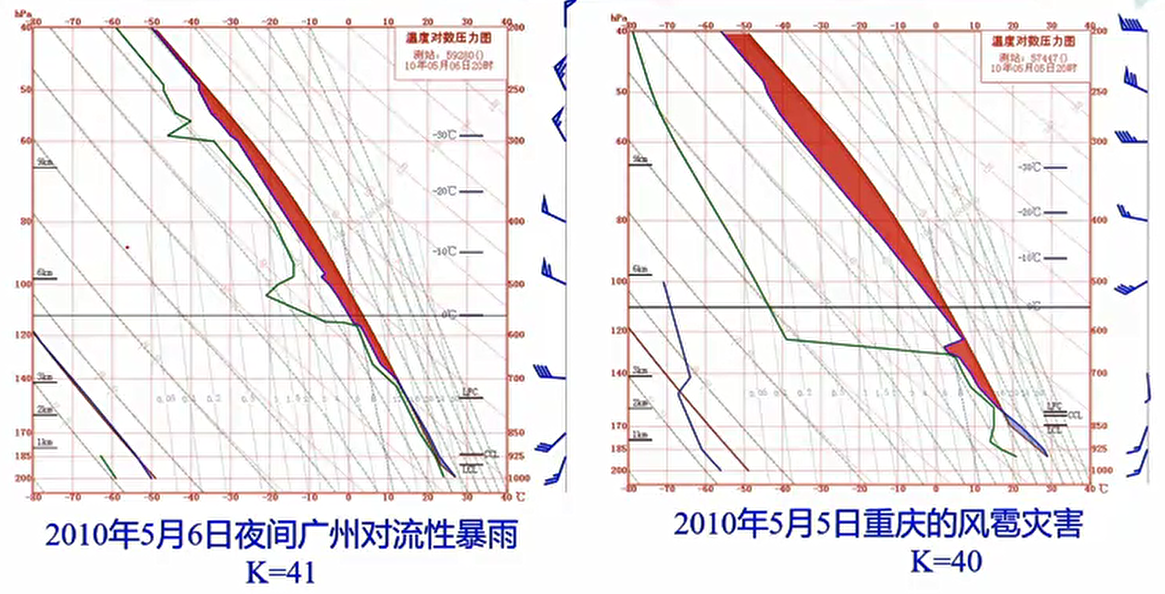
image

如上图的两张 T-lnP 图的 K 指数相近，但左边的是强对流暴雨，右边的是风雹天气。这是因为 K 指数无法无法反映中高层的湿度特征（与第一个问题的原因一样），左边整层都比较湿，而右边有大片的干层（而且干层的起始高度比第一个问题的要高），所以才会出现不同的对流现象。

13.4.3 改进的K指数

\[\mathrm{K} = 0.5(T_0 + T_{850}) + 0.5(T_{d0} + T_{d850}) - T_{500} - (T - T_d)_{700} \]

改进的K指数考虑了地面温度状况，这里 \(T_0\) 表示地面温度。\(\mathrm{K}\) 值越大表示气团低层越暖湿，稳定度越小，因而越有利于对流产生。

13.5 总指数（Total Totals, TT）

TT 指数被定义为：

\[\mathrm{TT} = T_{850} + T_{d850} - 2 T_{500} \]

单位为 ℃，\(T_{850} - T_{500}\) 为垂直温度直减率（vertical totals），\(T_{d850} - T_{500}\) 为 cross totals，所以

\[\mathrm{TT = vertical totals + cross totals} \]

TT 指数与对流发生程度的关系如下表：

TT 对流发生程度
TT<44 不太可能发生对流
44<TT<50 可能发生对流
51<TT<52 零星雷暴
53<TT<56 分散雷暴
TT>56 成片雷暴

13.6 深对流指数（DCI）

深对流指数是描述对流层中低层稳定度情况，反映不稳定和对流潜势的物理量。利用云顶相当黑体亮温计算的深对流指数可以作为表示云顶等于或高于 400hPa 深对流云的指数，其计算公式为：

\[\mathrm{DCI} = T_{850} + T_{d850} - \mathrm{LI} \]

深对流指数将 850hPa 层的温度与地面至 500hPa 的浮力特性结合，估计发生深对流潜势。该指数很高的地方，若同时具备抬升气块的触发机制，则很可能出现强对流天气事件。

参考资料

posted @ 2024-07-13 11:23  漫舞八月（Mount256）  阅读(115)  评论(0)  编辑  收藏  举报