大气热力学（8）——热力学图的应用之一（气象要素求解）
本篇文章源自我在 2021 年暑假自学大气物理相关知识时手写的笔记，现转化为电子版本以作存档。相较于手写笔记，电子版的部分内容有补充和修改。笔记内容大部分为公式的推导过程。
8.1 复习斜 T-lnP 图上的几种线
现在我们在斜 T-lnP 图上接触了几种线，让我们来复习一下吧。
8.1.1 等温线和等压线
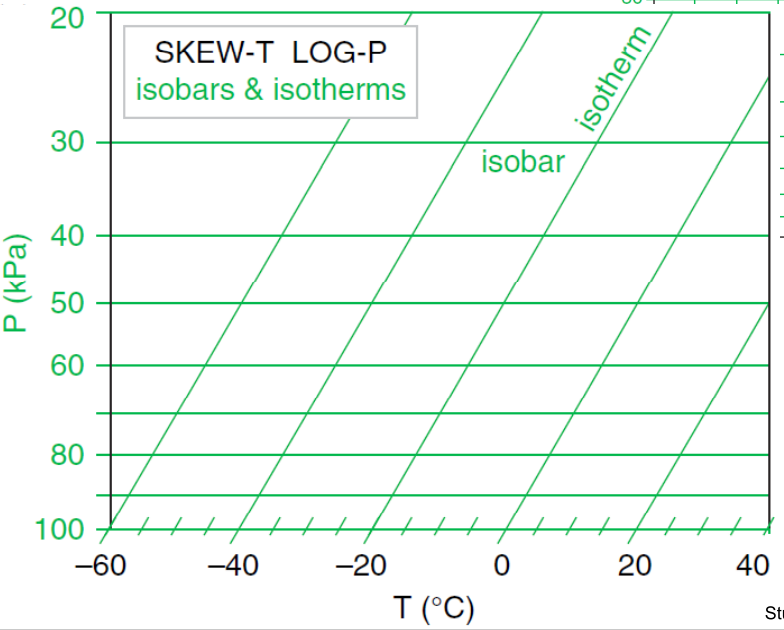
8.1.2 干绝热线
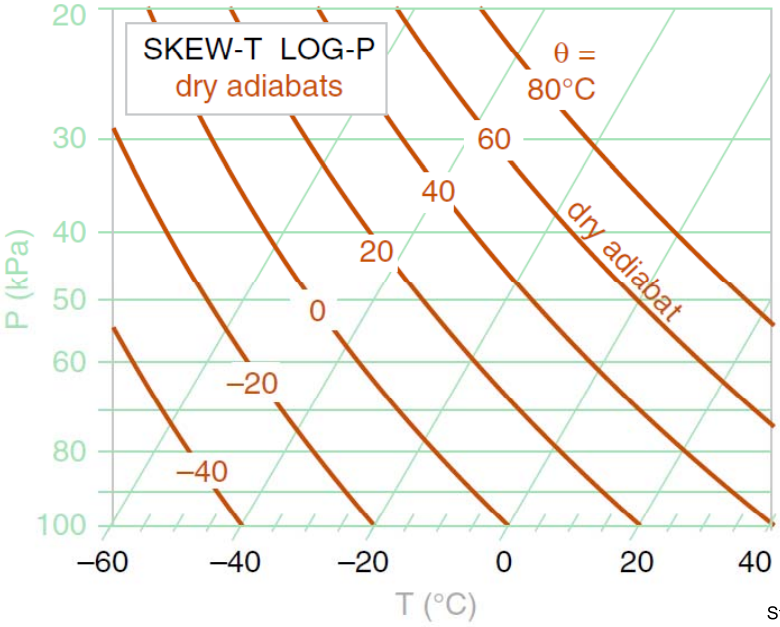
8.1.3 湿绝热线
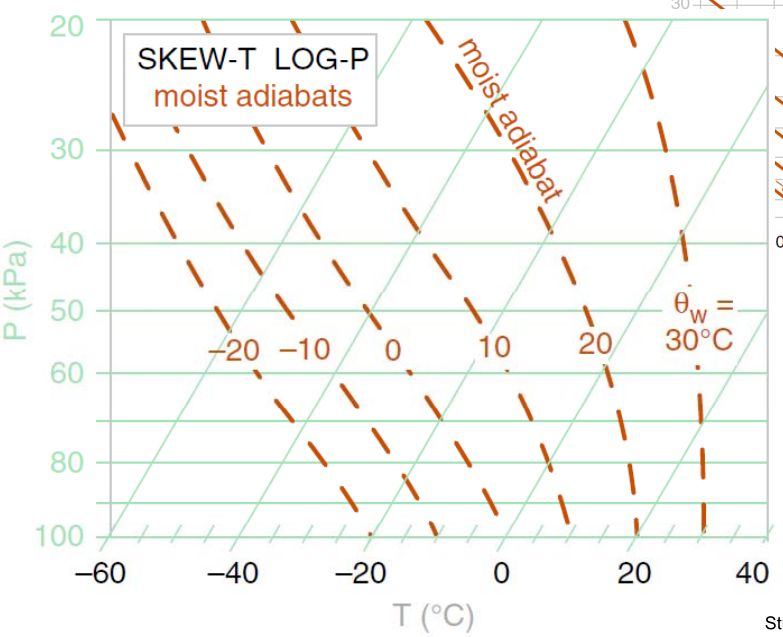
8.1.4 等饱和比湿线
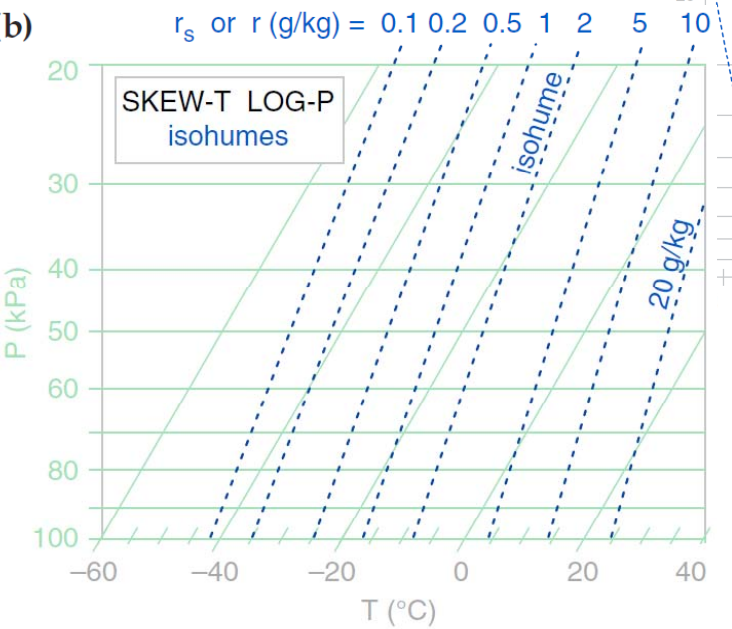
现在来看看 T-lnP 图的一些实际应用。
8.2 热力学图的简单应用
8.2.1 求抬升凝结高度
【例】温度 20℃，露点 6℃ 的气块从 1000hPa 高度抬升。求抬升凝结高度（LCL）及气块到该高度时的温度和位温。
【解】使用斜 T-lnP 图，先从图中找到四种线：等温线、干绝热线、湿绝热线、等饱和比湿线，如下图所示：
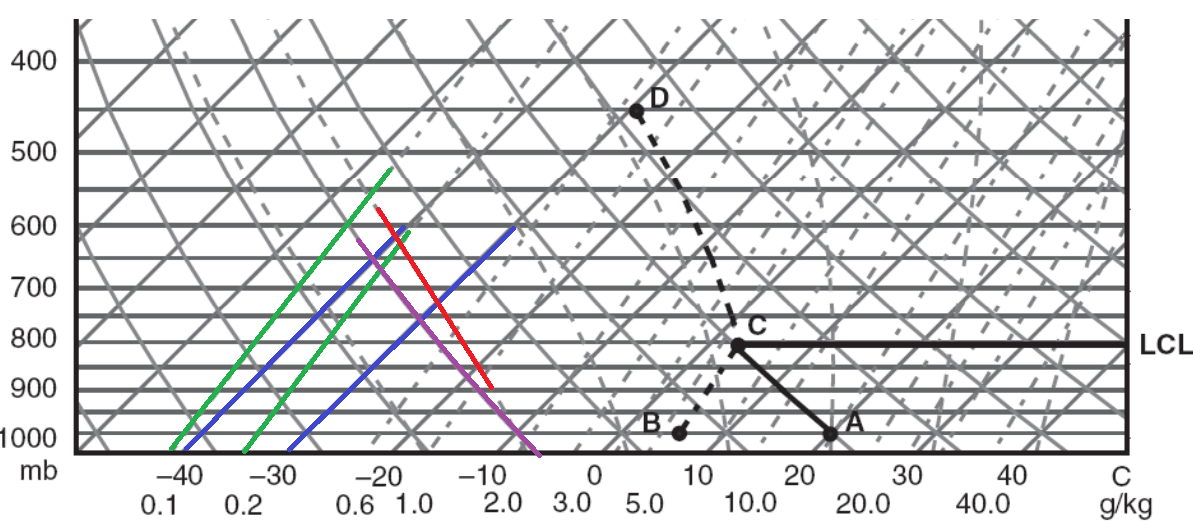
蓝色线是等温线，绿色线是等饱和比湿线，紫色线是干绝热线，红色线是湿绝热线。根据定义，1000 hPa 高度处气块所具有的温度即为位温，所以该气块的位温就是 20℃（本题的一大坑点：位温表示的是气块的热力性质，与高度无关！）。
现在来求气块的抬升凝结高度。先找到横坐标上露点温度 \(T_d\) 为 6℃ 的点，注意要沿着等饱和比湿线 BC 上升；再找到气压为 1000hpa、温度为 20℃ 的点 A，沿着干绝热线 AC 上升。两者交汇处 C 点即为气块的抬升凝结高度，此时气块已经饱和。从 C 点处沿着等压线可读出抬升凝结高度 LCL 为 800hpa；从 C 点处沿着等温线可读出该高度的气块温度为 3℃。
另外需要注意的是，若饱和气团继续上升，则需沿着湿绝热线 CD 上升。
8.2.2 求露点温度
【例】1000hPa 高度一气块温度为 298K，水汽混合比为 14g/kg。求气块的相对湿度和露点温度。
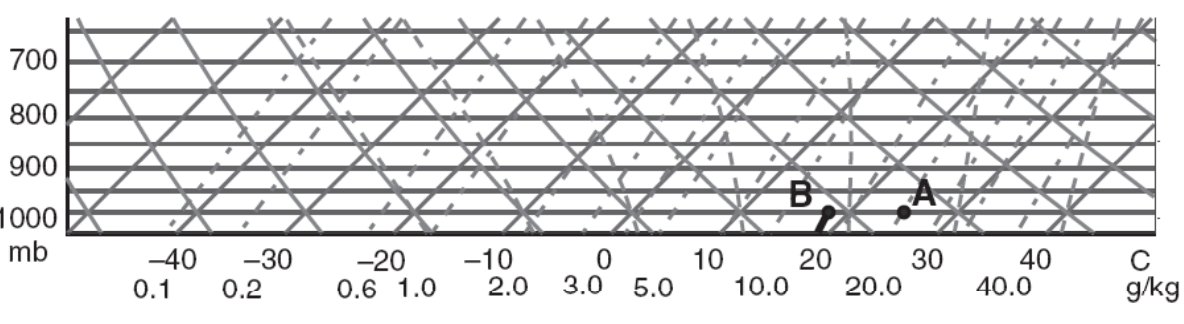
【解】这是一个静态的过程，不涉及气块的上升或下降。水汽混合比为 14g/kg，则在横坐标中找到 14g/kg 的点，然后沿着等饱和比湿线上升到 B 点（此处高度为 1000hPa）。此时从 B 点沿着等温线即可读出露点温度为 19℃。
298K 等于 25℃，则在横坐标中找到 25℃ 的点，然后沿着等温线上升到 A 点（此处高度为 1000hPa）。此时从 A 点沿着等饱和比湿线即可读出比湿为 29g/kg。于是相对湿度为 14/20 = 70%。
8.2.3 求气块上升到特定高度时的温度
【例】温度 20℃，露点 6℃ 的气块从 1000hPa 高度抬升，求气块抬升至 450hPa 时的温度。
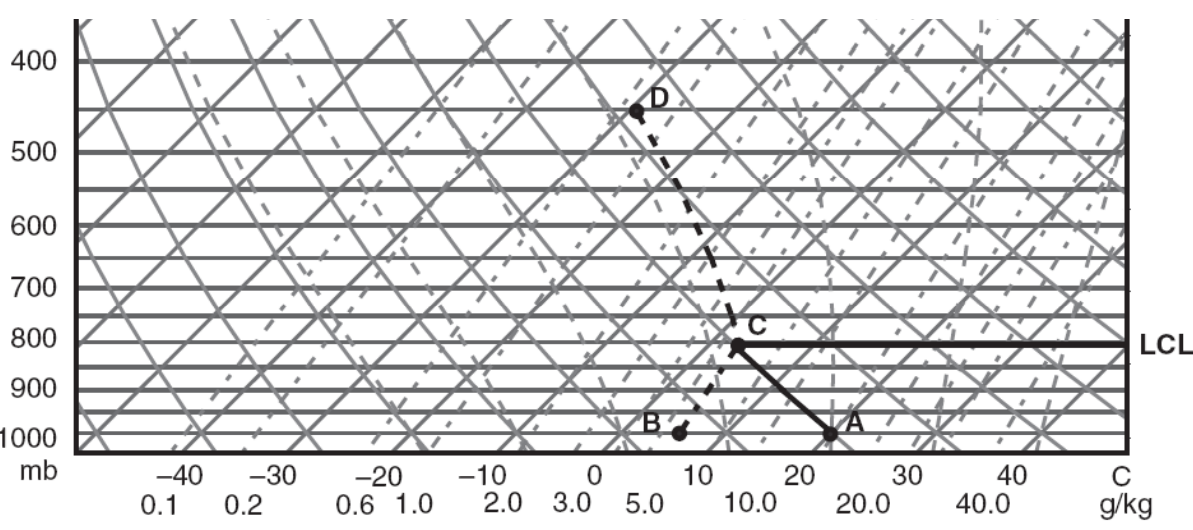
【解】本题就是 8.2.1 节中的题目修改而来。先找到横坐标上露点温度 \(T_d\) 为 6℃ 的点，注意要沿着等饱和比湿线 BC 上升；再找到气压为 1000hpa、温度为 20℃ 的点 A，沿着干绝热线 AC 上升。两者交汇处 C 点即为气块的抬升凝结高度，此时气块已经饱和。饱和气团继续上升，则沿着湿绝热线 CD 上升至 D 点（450hpa 处），从 D 点沿着等温线可读出此时气块温度为 -29℃。
8.2.4 求相当位温和凝结水量
【例】800hPa 饱和气块温度为 −10℃。求：（1）相当位温；（2）气块被抬升到 425hPa 过程中凝结的水量。
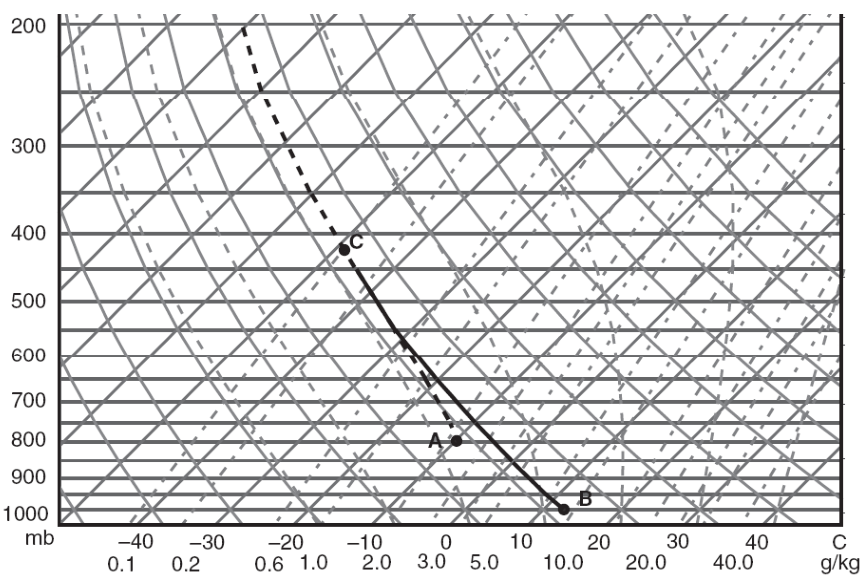
【解】由气压 800hPa 和气块温度 −10℃ 在图中找到 A 点，此点即为气块的初始状态。此处沿着等饱和比湿线可读出比湿为 2.2g/kg。
饱和气块沿着湿绝热线上升到 C 点（此处气压为 425hPa），此处沿着等饱和比湿线可读出比湿为 0.1g/kg。在这个湿绝热过程中，气块凝结的水量为 2.2 - 0.1 = 2.1g/kg。
关于相当位温的求法，其实在 6.3 节中就已经介绍过了，这里再复习一下：湿空气绝热上升至所含水汽全部凝结脱落（假绝热过程），所含潜热全部释放后，再按干绝热过程下降到 1000hPa 时气块所具有的温度，就是相当位温。从 C 点沿着干绝热线下降到 B 点（此处气压为 1000hPa）。沿着等温线读出此时温度为 13℃，即为此气块的相当位温。
8.2.5 求特定高度的湿球温度
这里暂时没有找到相关例题，不过我们可以给出其求解方法：
- 从该气压层的温度出发，让气块从该气压层沿着干绝热曲线上升直到与该气压层露点温度（需从露点曲线读出）对应的等饱和比湿线相交；
- 然后从两线交点处沿着湿绝热线下降到气块的起始气压高度，所对应的温度即为该气压层的湿球温度。
如果我们对不同气压层重复上述过程，则可得到不同气压层的湿球温度，将这些湿球温度点连接起来，则可得到湿球温度曲线（即湿球温度垂直廓线）。
在后面文章中，我们还会提及层结曲线（即温度廓线）和状态曲线。层结曲线是根据实际探空测得的数据而绘制，而状态曲线是根据露点温度、假定气块作绝热上升过程而绘制出来的。
