大气热力学（6）——位温和假相当位温

本篇文章源自我在 2021 年暑假自学大气物理相关知识时手写的笔记，现转化为电子版本以作存档。相较于手写笔记，电子版的部分内容有补充和修改。笔记内容大部分为公式的推导过程。

目录

• 6.1 位温
• 6.2 斜 T-lnP 图（Skew T-lnP）
  • 6.2.1 等温线的绘制
  • 6.2.2 干绝热线的绘制
• 6.3 假相当位温
• 6.4 假相当温度
• 6.5 各种温度的总结

6.1 位温

空气块在干绝热过程中，其温度是变化的，同一气块处于不同的气压（高度）时，其温度值常常是不同的，这就给处在不同高度上的两气块进行热状态的比较带来一定困难。

为此，假设把气块都按干绝热过程移到同一高度（或等压面上），就可以进行比较了。把各层中的气块循着干绝热的程序订正到一个标准高度：1000hPa 处，这时所具有的温度称为位温，以 \(\theta\) 表示。以下是位温表达式的推导。

先写出干绝热方程（泊松方程）得：

\[\frac{T}{T_0} = \bigg(\frac{p}{p_0} \bigg)^{0.286} \]

把 \(T = \theta，p = 1000\) 代入，即可得到位温的表达式：

\[\theta = T_0 \bigg(\frac{1000}{p_0} \bigg)^{0.286} \]

式中，\(T_0\) 和 \(p_0\) 是干绝热过程起始时刻的温度和气压。此式表明，气块沿干绝热线升降时，位温恒定不变（或者说位温守恒），因此干绝热线也称为等位温线。

我们把上式整理成：

\[p_0^{0.286} = \bigg( \frac{1000^{0.286}} {\theta} \bigg) T_0 \]

我们发现，对任一 \(\theta\) 常数值，上式符合一个正比例函数 \(y=kx\)：

• \(y\) 对应 \(p_0^{0.286}\)
• \(k\) 对应 \(( \frac{1000^{0.286}} {\theta} )\)
• \(x\) 对应 \(T_0\)

每个 \(\theta\) 值都可以用一条干绝热线表示，且一定通过点 \(p_0=0，T_0=0\)。若使用前文所述的 T-lnP 图，则不同 \(\theta\) 值对应的干绝热线如下图所示：

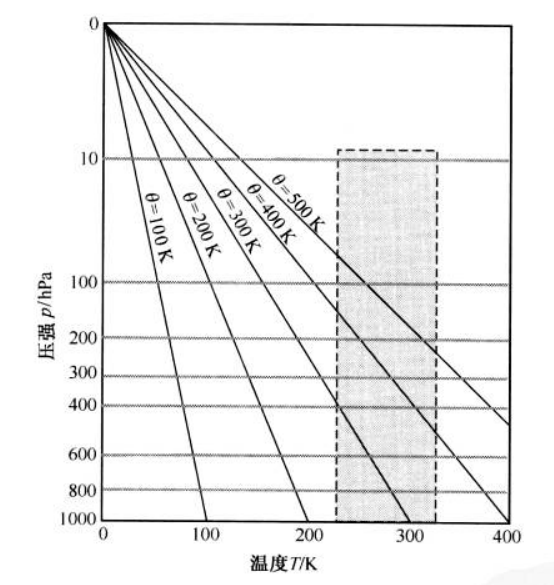
在这张图中，等温线是垂直的（即垂直于 \(x\) 轴），干绝热线相对于等温线成锐角。注意，此处使用的 T-lnP 图并不是常用的 T-lnP 图，因为其纵坐标的尺度是 \(-0.286 \ln p\)。

在国内气象台中，T-lnP 图是比较常用的。但在国外，他们却并不使用这种图，原因是大多数探空数据都集中于上图的灰色狭小区域，不便使用。于是人们对上图进行了改良，将等温线变成倾斜的直线，从而产生了斜 T-lnP（skew T-lnP）图。

6.2 斜 T-lnP 图（Skew T-lnP）

6.2.1 等温线的绘制

在斜 T-lnP 图中，纵坐标依然为 \(y = -\ln p\)，横坐标为：

\[x = T + my = T - m\ln p \]

其中 \(m\) 是一个可人为设定的常数，\(T\) 是等温过程的温度。上式又可写成：

\[y = \frac{x - T}{m} \]

即：

\[ -\ln p = \frac{1}{m} x - \frac{T}{m} \]

注意，这个 \(T\) 是等温过程的温度，是一个常数，所以上式可视为一个一次方程：

\[ -\ln p = c_1x + c_2(T) \]

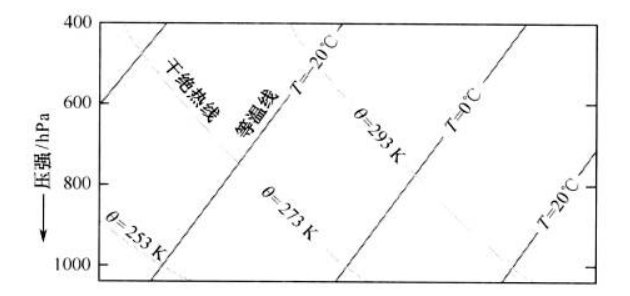
其中，\(c_1\) 是人为设定的常数，无论什么等温过程都不会变化；而 \(c_2(T)\) 为对每个等温过程的不同常数，是关于 \(T\) 的常数。我们一般令 \(c_1=1\)，因此，等温线在斜 T-lnP 图上是一条从左到右的倾斜 45° 的直线，如下图的黑色实线所示：

6.2.2 干绝热线的绘制

为了说明斜 T-lnP 图是怎样表示干绝热线的，我们先写出位温的表达式：

\[p^{0.286} = \bigg( \frac{1000^{0.286}} {\theta} \bigg) T \]

如果对上式两边取对数：

\[0.286 \ln p = (0.286 \ln 1000 - \ln \theta) + \ln T \\ 整理得：-\ln p = -\frac{1}{0.286} \ln T - \frac{0.286 \ln 1000 - \ln \theta}{0.286} \]

把上式视为一次函数，自变量为 \(\ln T\)，因变量为 \(-\ln p\)，则变成：

\[-\ln p = c_1 \ln T - c_2(\theta) \]

其中，\(c_1\) 是常数，\(c_2(\theta)\) 是关于 \(\theta\) 的常数。如果在一个以 \(\ln T\) 为横坐标、以 \(-\ln p\) 为纵坐标的图上绘制这条曲线，则干绝热线就是直线。

但是，在斜 T-lnP 图中，纵坐标依然为 \(-\ln p\)，但横坐标不是 \(\ln T\)，而是 \(T\)。所以在斜 T-lnP 图上，干绝热线起始于图的右下方，终止于图的左上方，是稍有向下弯曲的一组线，在下图中淡淡的虚线即为一组干绝热线（可能很难看得清）：

干空气团的上升过程，在图中可以表现为：沿着某条干绝热线从底部一直往上，随着高度的上升而降温，直到其相对湿度变为 100%（即空气变得饱和）后不再适用该线，而是使用湿绝热线。比如，若某团干空气的位温为 \(\theta = 273 \mathrm{K}\)，则该气团的上升相当于沿着位温为 \(273 \mathrm{K}\) 的干绝热线向上画。

6.3 假相当位温

在气块的假绝热过程中，当气块中含有的水汽全部凝结降落时，所释放的潜热，就使原气块的位温提高到了极值（提升的大小即为 \(\frac{L q_s}{C_{p,m}}\)），这个数值称为假相当位温，用 \(\theta_{se}\) 表示，定义如下：

\[\begin{aligned} \theta_{se} &= \theta \cdot \exp \bigg(\frac{L q_s}{C_{p,m} T_c} \bigg) \\ &\approx \theta \bigg(1 + \frac{L q_s}{C_{p,m} T_c} \bigg) \\ &\approx \theta + \frac{L q_s}{C_{p,m}} \\ &= T_0 \bigg(\frac{1000}{p_0} \bigg)^{0.286} + \frac{L q_s}{C_{p,m}} \end{aligned} \]

式中，\(q_s\) 是气块在 1000hPa 处，1g 湿空气所含水汽量；\(T_c\) 是抬升凝结高度处的温度。第二步实际上是利用了高阶无穷小的展开，第三步作了假设 \(\theta = T_c\)。由上式可以看出 \(\theta_{se}\) 是气压、温度和湿度的函数。

我们可以从 T-lnP 图中求得某气块的假相当位温。如下图所示，设有一气块，其温、压、湿分别为 \((p, T, q)\)。

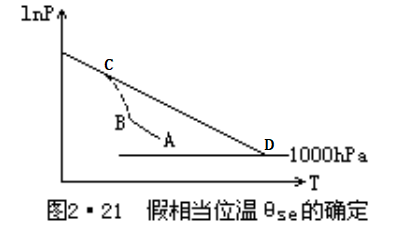
• 在图上温度、压力始于 A 点，这时气块是未饱和的，令其沿干绝热线上升到达抬升凝结高度 B 点，这时气块达到饱和；
• 当气块再继续上升时，就不断地有水汽凝结，这时它将沿湿绝热线上升降温，到达 C 点（这个 C 点如何确定？后面文章将会详细提及）；
• 在 C 点处，气块内水汽已全部凝结降落，再令其沿干绝热线下沉到 1000hPa（D 点），此时气块的温度（需沿着等温线读数）就是假相当位温 \(\theta_{se}\)。

假相当位温不仅考虑了气压对温度的影响，而且也考虑了水汽对温度的影响，实际上是关于温度、压力、湿度的综合特征量，对于干绝热、假绝热和湿绝热过程都具有保守性。

6.4 假相当温度

类似于位温与温度的关系：

\[\theta = T \bigg(\frac{1000}{p} \bigg)^{0.286} \]

假相当位温 \(\theta_{se}\) 与假相当温度 \(T_{se}\) 也有类似的关系：

\[\theta_{se} = T_{se} \bigg(\frac{1000}{p} \bigg)^{0.286} \]

因此，假相当温度可定义为：令气块干绝热上升（干绝热线），到达凝结高度后又按假绝热过程上升（湿绝热线），直到所有水汽耗尽，再沿干绝热线过程下降到原来的气压处所应有的温度。

6.5 各种温度的总结

温湿参量	符号表示	物理意义	干绝热是否守恒	湿绝热是否守恒
温度	\(T\)	（略）	-	-
位温	\(\theta\)	把气块按干绝热过程移到 1000hPa 处，此时气块所具有的温度	是	否
相当温度	\(T_e\)	等压过程中湿空气中水汽全部凝结，并释放的潜热使空气达到的温度	否	否
相当位温	\(\theta_e\)	（比较少用的物理量，在国外文献一般都是指假相当位温）	否	否
假相当温度	\(T_{se}\)	气块干绝热上升，到达凝结高度后湿绝热上升，直到所有水汽耗尽，再干绝热线下降到原来的气压处所应有的温度	否	否
假相当位温	\(\theta_{se}\)	气块干绝热上升，到达凝结高度后湿绝热上升，直到所有水汽耗尽，再干绝热线下降到 1000hPa 处所应有的温度	是	是