【深度学习】神经网络的建立与推理

目录

• 神经网络（neural network）的结构
• 神经元中常用的激活函数（activation function）
• 神经网络的表示
• 神经网络的代码实现
• 使用已学习完毕的神经网络进行推理（inference）

源代码文件请点击此处！

神经网络（neural network）的结构

• 输入层（input layer）：第 0 层（layer 0）
• 隐藏层（hidden layer）：第 1 层（layer 1）、第 2 层（layer 2）、······、第 \(l-1\) 层（layer \(l-1\)）
• 输出层（output layer）：第 \(l\) 层（layer \(l\)）

神经元中常用的激活函数（activation function）

• 线性激活函数（linear activation function）（用于线性回归）：输出可正可负，相当于没有使用激活函数，所以不能使用该函数作为激活函数！

\[g(z) = z \]

• ReLU（rectified linear unit）函数（用于线性回归）：输出为非负，常用于神经网络的隐藏层

\[g(z) = \max (0, z) = \begin{cases} 0, z < 0 \\ z, z \geq 0 \end{cases} \]

• sigmoid 函数（用于二元分类/逻辑回归）：输出只能为正，常用于神经网络的输出层

\[g(z) = \frac{1}{1+e^{-z}} = P(\hat{y} = 1 | \vec{x}) \]

• softmax 函数（用于多元分类）：常用于神经网络的输出层

\[g(z_{i}) = \frac{e^{z_i}}{\sum_{j=1}^{N}e^{z_j}} = P(\hat{y} = i | \vec{x}) \]

• 改良的 softmax 函数：指数运算的结果容易过大而导致溢出，因此可进行如下改进：

\[\begin{aligned} g(z_{i}) &= \frac{e^{z_i}}{\sum_{j=1}^{N}e^{z_j}} \\ &= \frac{Ce^{z_i}}{C\sum_{j=1}^{N}e^{z_j}} \\ &= \frac{e^{z_i + \ln C}}{\sum_{j=1}^{N}e^{z_j + \ln C}} \\ &= \frac{e^{z_i + C'}}{\sum_{j=1}^{N}e^{z_j + C'}} \\ \end{aligned} \]

为防止溢出，一般 \(C'\) 取输入信号的最大值。

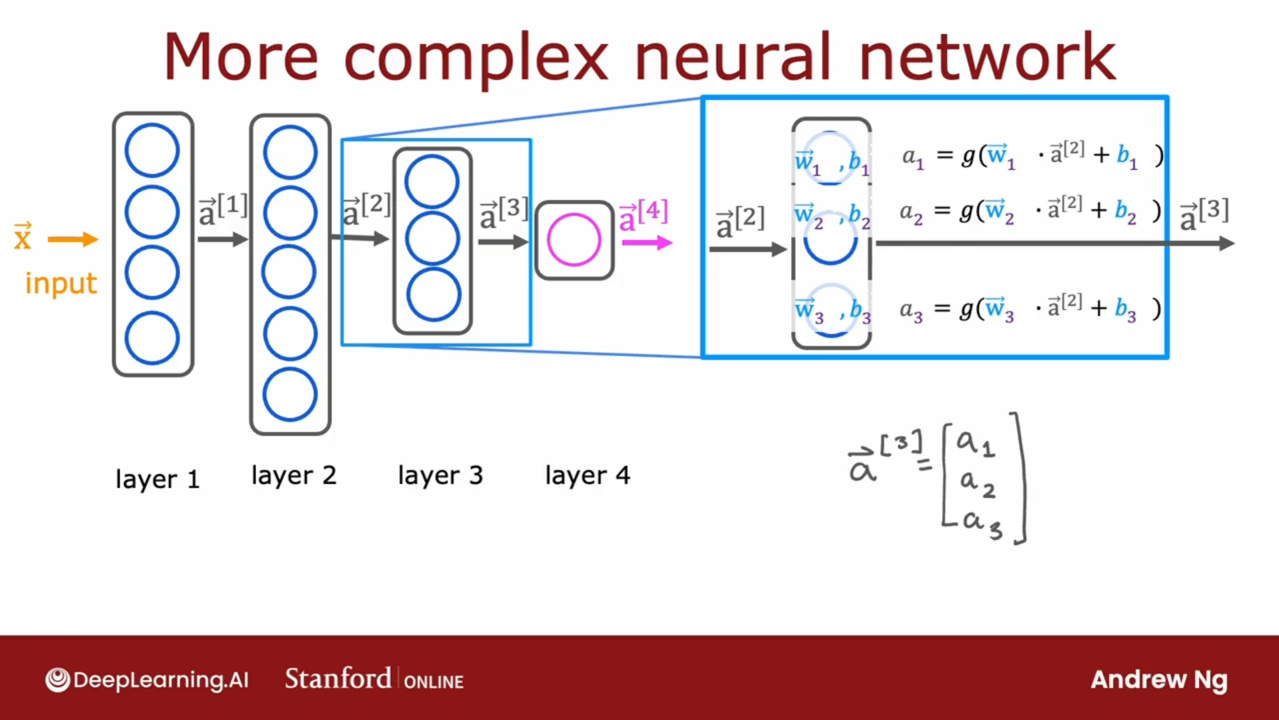
神经网络的表示

继续以上图为例（设神经元的激活函数为 \(g(z)\)）：

• 输入层：\(\vec{x} = \vec{a}^{[0]} = (a^{[0]}_1, a^{[0]}_2)\)
• 第 1 层：输入 \(\vec{a}^{[0]} = (a^{[0]}_1, a^{[0]}_2)\)，输出 \(\vec{a}^{[1]} = (a^{[1]}_1, a^{[1]}_2, a^{[1]}_3, a^{[1]}_4)\)
  • \(a^{[1]}_1 = g(\vec{w}^{[1]}_1 \cdot \vec{a}^{[0]} + b^{[1]}_1)\)
  • \(a^{[1]}_2 = g(\vec{w}^{[1]}_2 \cdot \vec{a}^{[0]} + b^{[1]}_2)\)
  • \(a^{[1]}_3 = g(\vec{w}^{[1]}_3 \cdot \vec{a}^{[0]} + b^{[1]}_3)\)
  • \(a^{[1]}_4 = g(\vec{w}^{[1]}_4 \cdot \vec{a}^{[0]} + b^{[1]}_4)\)
  • 矩阵形式：令 \(W^{[1]} = (\vec{w}^{[1]}_1, \vec{w}^{[1]}_2, \vec{w}^{[1]}_3, \vec{w}^{[1]}_4)_{2 \times 4}\)，\(B^{[1]} = (b^{[1]}_1, b^{[1]}_2, b^{[1]}_3, b^{[1]}_4)_{1 \times 4}\)，则 \(\vec{a}^{[1]} = g(\vec{a}^{[0]} W^{[1]} + B^{[1]})\)
• 第 2 层：输入 \(\vec{a}^{[1]} = (a^{[1]}_1, a^{[1]}_2, a^{[1]}_3, a^{[1]}_4)\)，输出 \(\vec{a}^{[2]} = (a^{[2]}_1, a^{[2]}_2, a^{[2]}_3, a^{[2]}_4, a^{[2]}_5)\)
  • \(a^{[2]}_1 = g(\vec{w}^{[2]}_1 \cdot \vec{a}^{[1]} + b^{[2]}_1)\)
  • \(a^{[2]}_2 = g(\vec{w}^{[2]}_2 \cdot \vec{a}^{[1]} + b^{[2]}_2)\)
  • \(a^{[2]}_3 = g(\vec{w}^{[2]}_3 \cdot \vec{a}^{[1]} + b^{[2]}_3)\)
  • \(a^{[2]}_4 = g(\vec{w}^{[2]}_4 \cdot \vec{a}^{[1]} + b^{[2]}_4)\)
  • \(a^{[2]}_5 = g(\vec{w}^{[2]}_5 \cdot \vec{a}^{[1]} + b^{[2]}_5)\)
  • 矩阵形式：令 \(W^{[2]} = (\vec{w}^{[2]}_1, \vec{w}^{[2]}_2, \vec{w}^{[2]}_3, \vec{w}^{[2]}_4, \vec{w}^{[2]}_5)_{4 \times 5}\)，\(B^{[2]} = (b^{[1]}_1, b^{[1]}_2, b^{[1]}_3, b^{[1]}_4, b^{[1]}_5)_{1 \times 5}\)，则 \(\vec{a}^{[2]} = g(\vec{a}^{[1]} W^{[2]} + B^{[2]})\)
• 第 3 层：输入 \(\vec{a}^{[2]} = (a^{[2]}_1, a^{[2]}_2, a^{[2]}_3, a^{[2]}_4, a^{[2]}_5)\)，输出 \(\vec{a}^{[3]} = (a^{[3]}_1, a^{[3]}_2, a^{[3]}_3)\)
  • \(a^{[3]}_1 = g(\vec{w}^{[3]}_1 \cdot \vec{a}^{[2]} + b^{[3]}_1)\)
  • \(a^{[3]}_2 = g(\vec{w}^{[3]}_2 \cdot \vec{a}^{[2]} + b^{[3]}_2)\)
  • \(a^{[3]}_3 = g(\vec{w}^{[3]}_3 \cdot \vec{a}^{[2]} + b^{[3]}_3)\)
  • 矩阵形式：令 \(W^{[3]} = (\vec{w}^{[3]}_1, \vec{w}^{[3]}_2, \vec{w}^{[3]}_3)_{5 \times 3}\)，\(B^{[3]} = (b^{[3]}_1, b^{[3]}_2, b^{[3]}_3)_{1 \times 3}\)，则 \(\vec{a}^{[3]} = g(\vec{a}^{[2]} W^{[3]} + B^{[3]})\)
• 第 4 层：输入 \(\vec{a}^{[3]} = (a^{[3]}_1, a^{[3]}_2, a^{[3]}_3)\)，输出 \(\vec{a}^{[4]} = (a^{[4]}_1)\)
  • \(a^{[4]}_1 = g(\vec{w}^{[4]}_1 \cdot \vec{a}^{[3]} + b^{[4]}_1)\)
  • 矩阵形式：令 \(W^{[4]} = (\vec{w}^{[4]}_1)_{3 \times 1}\)，\(B^{[4]} = (b^{[3]}_1,)_{1 \times 1}\)，则 \(\vec{a}^{[4]} = g(\vec{a}^{[3]} W^{[4]} + B^{[4]})\)
• 第 \(l\) 层：输入 \(\vec{a}^{[l-1]} = (..., a^{[l-1]}_j, ...)\)，输出 \(\vec{a}^{[l]} = (..., a^{[l]}_j, ...)\)
  • \(a^{[l]}_j = g(\vec{w}^{[l]}_j \cdot \vec{a}^{[l-1]} + b^{[l]}_j)\)

神经网络的代码实现

以上图为例：

import numpy as np

# sigmoid 函数
def sigmoid_function(x):
    return 1 / (1 + np.exp(-x))

# softmax 函数
def softmax_function(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

# 改良的 softmax 函数（防止在指数运算时发生溢出）
def softmax_function_trick(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

# ReLU 函数
def relu_function(x):
    return np.maximum(0, x)

# 线性激活函数（恒等函数）
def linear_activation_function(x):
    return x

# 初始化配置各个神经元的参数
def init_network():
    network = {} # 字典类型

    # 隐藏层第 1 层（layer 1）：一共 4 个神经元
    network['W1'] = np.array([[0.1, 0.2, 0.3, 0.4],
                              [0.5, 0.6, 0.7, 0.8]])
    network['B1'] = np.array([[0.1, 0.2, 0.3, 0.4]])

    # 隐藏层第 2 层（layer 2）：一共 5 个神经元
    network['W2'] = np.array([[0.1, 0.2, 0.3, 0.4, 0.5],
                              [0.6, 0.7, 0.8, 0.9, 1.0],
                              [0.1, 0.2, 0.3, 0.4, 0.5],
                              [0.6, 0.7, 0.8, 0.9, 1.0]])
    network['B2'] = np.array([[0.1, 0.2, 0.3, 0.4, 0.5]])

    # 隐藏层第 3 层（layer 3）：一共 3 个神经元
    network['W3'] = np.array([[0.1, 0.2, 0.3],
                              [0.4, 0.5, 0.6],
                              [0.7, 0.8, 0.9],
                              [0.6, 0.7, 0.8],
                              [0.1, 0.2, 0.3]])
    network['B3'] = np.array([[0.1, 0.2, 0.3]])

    # 隐藏层第 4 层（layer 4）：一共 1 个神经元
    network['W4'] = np.array([[0.1],
                              [0.2],
                              [0.3]])
    network['B4'] = np.array([[0.1]])

    return network

# 神经元的内部实现：输入A，权重W，偏置B，激活函数g()，输出A_out
def dense(A, W, B, g):
	Z = np.matmul(A, W) + B # 这里是矩阵乘法，而非点乘
	A_out = g(Z)
	return A_out

# 神经网络的搭建
def predict(network, X):
    W1, W2, W3, W4 = network['W1'], network['W2'], network['W3'], network['W4']
    B1, B2, B3, B4 = network['B1'], network['B2'], network['B3'], network['B4']

    A1 = dense(X, W1, B1, sigmoid_function) # layer 1
    A2 = dense(A1, W2, B2, sigmoid_function) # layer 2
    A3 = dense(A2, W3, B3, sigmoid_function) # layer 3
    A4 = dense(A3, W4, B4, linear_activation_function) # layer 4

    return A4

# 从这里开始执行
if __name__ == '__main__':
    network = init_network() # 配置神经网络的参数
    X = np.array([[1.0, 0.5]]) # 输入层（layer 0）
    Y = predict(network, X) # 输出层（layer 4）
    print(Y)

使用已学习完毕的神经网络进行推理（inference）

• 测试集：源自 MNIST 数据集（研究手写数字识别的数据集），数据集的下载脚本位于代码仓库的 /dataset/mnist.py
• one-hot 表示：将正确解标签表示为 1，其他错误解标签表示为 0 的表示方法，例如：

# y: 图像数据经过神经网络计算后的输出结果，对应数字 0~9 的概率，即“0”的概率为 0.1，“2”的概率最高，为 0.6
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
# t: 监督数据，将正确解标签表示为 1，其他错误解标签表示为 0，这里正确解对应数字“2”
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]

• 代码执行流程：

  • 第一次调用函数 load_mnist 时，会自动下载 MNIST 数据集并转换为字典类型的数据，并创建文件 mnist.pkl；以后再调用时，会直接读入该文件，节省时间
  • 调用函数 init_network，这里读入文件 sample_weight.pkl，内容为已学习好的神经网络参数（至于如何学习到这些参数会在下一篇介绍）
  • 对 MNIST 中的每个图像数据，调用函数 predict，用上述参数构建神经网络，对该图像进行推理（具体是对 0 到 9 依次给出一个概率，概率最高的数字 x 说明图像最有可能是数字 x）
  • 与正确解标签进行对比，统计正确分类的个数，并得出精度结果

• 代码实现：

# coding: utf-8

import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import pickle
from dataset.mnist import load_mnist

# ============================= activation functions ===================================

# sigmoid 函数
def sigmoid_function(x):
    return 1 / (1 + np.exp(-x))

# softmax 函数
def softmax_function(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

# 改良的 softmax 函数（防止在指数运算时发生溢出）
def softmax_function_trick(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

# ReLU 函数
def relu_function(x):
    return np.maximum(0, x)

# 线性激活函数（恒等函数）
def linear_activation_function(x):
    return x

# ============================= neural network ===================================

# 神经元的内部实现：输入A，权重W，偏置B，激活函数g()，输出A_out
def dense(A, W, B, g):
	Z = np.matmul(A, W) + B # 这里是矩阵乘法，而非点乘
	A_out = g(Z)
	return A_out

# 初始化配置各个神经元的参数，可直接导入记录了神经网络参数的pickle文件
def init_network(filename):
    with open(filename, 'rb') as f:
        network = pickle.load(f)
    return network

# 神经网络的搭建
def predict(network, X):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    B1, B2, B3 = network['b1'], network['b2'], network['b3']
    A1 = dense(X, W1, B1, sigmoid_function) # layer 1
    A2 = dense(A1, W2, B2, sigmoid_function) # layer 2
    A3 = dense(A2, W3, B3, softmax_function_trick) # layer 3
    return A3

# 获取训练集和测试集
def get_data():
    # 训练集数据和结果，测试集数据和结果
    # 参数说明：展开为一维数组，不使用归一化，不使用 one-hot 标签（直接使用 7，2 这样简单保存正确解标签）
    # 详细参数说明见代码仓库内的 dataset/mnist.py
    (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=True, one_hot_label=False)
    return x_train, t_train, x_test, t_test

# 模型评估
def assessment():
    pass

# ============================= main ===================================

if __name__ == '__main__':
    network = init_network('sample_weight.pkl') # 配置神经网络的参数
    _, _, X, T = get_data() # X：测试集数据，T：测试集正确结果
    accuracy_cnt = 0 # 记录推理正确的个数

    for i in range(X.shape[0]): # X.shape[0] 即为测试集数据个数
        Y = predict(network, X[i])  # 对测试集每个数据进行推理，得到 10 个概率数值的一维数组
        # print(Y)
        # axis=0：返回每一列最大值的索引；axis=1：返回每一行最大值的索引
        # axis=None：降为一维数组后，返回最大值的索引
        p = np.argmax(Y, axis=None) # 返回概率最大的索引
        if p == T[i]: # 如果推理结果与测试集结果相同，说明推理正确
            accuracy_cnt += 1

    print(f"accuracy: {float(accuracy_cnt) / X.shape[0]}") # 精度结果：93.52%