【机器学习】多元线性回归

目录

• 多元线性回归模型（multiple regression model）
• 损失/代价函数（cost function）——均方误差（mean squared error）
• 批量梯度下降算法（batch gradient descent algorithm）
• 特征工程（feature engineering）
• 特征缩放（feature scaling）
• 正则化线性回归（regularization linear regression）

源代码文件请点击此处！

多元线性回归模型（multiple regression model）

• 多元线性回归模型：

\[\begin{aligned} f_{\vec{w}, b}(\vec{x}) &= \vec{w} \cdot \vec{x} + b \\ &= w_1x_1 + w_2x_2 + ... + w_nx_n + b \\ &= \sum_{j=1}^{n} w_jx_j + b \end{aligned} \]

其中：

• \(\vec{w}\) 为权重（weight）= \((w_1, w_2, ..., w_n)\)，\(n\) 为向量维数
• \(b\) 为偏置（bias）
• \(\vec{x} = (x_1, x_2, ..., x_n)\)，\(n\) 为向量维数

损失/代价函数（cost function）——均方误差（mean squared error）

• 一个训练样本：\(\vec{x}^{(i)} = (x_1^{(i)}, x_2^{(i)}, ..., x_n^{(i)})\) 和 \(y^{(i)}\)
• 训练样本总数 = \(m\)
• 损失/代价函数：

\[\begin{aligned} J(\vec{w}, b) &= \frac{1}{2m} \sum^{m}_{i=1} [f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}]^2 \\ &= \frac{1}{2m} \sum^{m}_{i=1} [\vec{w} \cdot \vec{x}^{(i)} + b - y^{(i)}]^2 \end{aligned} \]

批量梯度下降算法（batch gradient descent algorithm）

• \(\alpha\)：学习率（learning rate），用于控制梯度下降时的步长，以抵达损失函数的最小值处。若 \(\alpha\) 太小，梯度下降太慢；若 \(\alpha\) 太大，下降过程可能无法收敛。
• 批量梯度下降算法：

\[\begin{aligned} repeat \{ \\ & tmp\_w_1 = w_1 - \alpha \frac{1}{m} \sum^{m}_{i=1} [f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}] x_1^{(i)} \\ & tmp\_w_2 = w_2 - \alpha \frac{1}{m} \sum^{m}_{i=1} [f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}] x_2^{(i)} \\ & ... \\ & tmp\_w_n = w_n - \alpha \frac{1}{m} \sum^{m}_{i=1} [f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}] x_n^{(i)} \\ & tmp\_b = b - \alpha \frac{1}{m} \sum^{m}_{i=1} [f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}] \\ & simultaneous \ update \ every \ parameters \\ \} until \ & converge \end{aligned} \]

• 检查梯度下降是否收敛（converge）：函数 \(J(\vec{w}, b)\) 随迭代次数的增加应逐渐减小。令 \(\epsilon = 0.001\)，若在某一次迭代中发现函数 \(J(\vec{w}, b)\) 的增长值 \(\leq \epsilon\)，则说明收敛。
• 实现代码：

import numpy as np
import matplotlib.pyplot as plt

# 计算误差均方函数 J(w,b)
def cost_function(X, y, w, b):
    m = X.shape[0] # 训练集的数据样本数
    cost_sum = 0.0
    for i in range(m):
        f_wb_i = np.dot(w, X[i]) + b
        cost = (f_wb_i - y[i]) ** 2
        cost_sum += cost
    return cost_sum / (2 * m)

# 计算梯度值 dJ/dw, dJ/db
def compute_gradient(X, y, w, b):
    m = X.shape[0] # 训练集的数据样本数（矩阵行数）
    n = X.shape[1] # 每个数据样本的维度（矩阵列数）
    dj_dw = np.zeros((n,))
    dj_db = 0.0
    for i in range(m): # 每个数据样本
        f_wb_i = np.dot(w, X[i]) + b
        for j in range(n): # 每个数据样本的维度
            dj_dw[j] += (f_wb_i - y[i]) * X[i, j]
        dj_db += (f_wb_i - y[i])
    dj_dw = dj_dw / m
    dj_db = dj_db / m
    return dj_dw, dj_db

# 梯度下降算法
def linear_regression(X, y, w, b, learning_rate=0.01, epochs=1000):
    J_history = [] # 记录每次迭代产生的误差值
    for epoch in range(epochs):
        dj_dw, dj_db = compute_gradient(X, y, w, b)
        # w 和 b 需同步更新
        w = w - learning_rate * dj_dw
        b = b - learning_rate * dj_db
        J_history.append(cost_function(X, y, w, b)) # 记录每次迭代产生的误差值
    return w, b, J_history

# 绘制散点图
def draw_scatter(x, y, title):
    plt.xlabel("X-axis", size=15)
    plt.ylabel("Y-axis", size=15)
    plt.title(title, size=20)
    plt.scatter(x, y)

# 打印训练集数据和预测值数据以便对比
def print_contrast(train, prediction, n):
    print("train  prediction")
    for i in range(n):
        print(np.round(train[i], 4), np.round(prediction[i], 4))

# 从这里开始执行
if __name__ == '__main__':
    # 训练集样本
    data = np.loadtxt("./data.txt", delimiter=',', skiprows=1)
    X_train = data[:, :4] # 训练集的第 0-3 列为 X = (x0, x1, x2, x3)
    y_train = data[:, 4] # 训练集的第 4 列为 y
    w = np.zeros((X_train.shape[1],)) # 权重
    b = 0.0 # 偏置
    epochs = 1000  # 迭代次数
    learning_rate = 1e-7  # 学习率
    J_history = []  # 记录每次迭代产生的误差值

    # 线性回归模型的建立
    w, b, J_history = linear_regression(X_train, y_train, w, b, learning_rate, epochs)
    print(f"result: w = {np.round(w, 4)}, b = {b:0.4f}")  # 打印结果

    # 训练集 y_train 与预测值 y_hat 的对比（这里其实我偷了个懒，训练集当测试集用，以后不要这样做！）
    y_hat = np.zeros(X_train.shape[0])
    for i in range(X_train.shape[0]):
        y_hat[i] = np.dot(w, X_train[i]) + b
    print_contrast(y_train, y_hat, y_train.shape[0])

    # 绘制误差值的散点图
    x_axis = list(range(0, epochs))
    draw_scatter(x_axis, J_history, "Cost Function in Every Epoch")
    plt.show()

特征工程（feature engineering）

将原有特征值通过组合或转化等方式变成新特征值。

特征缩放（feature scaling）

• 特征缩放的作用：

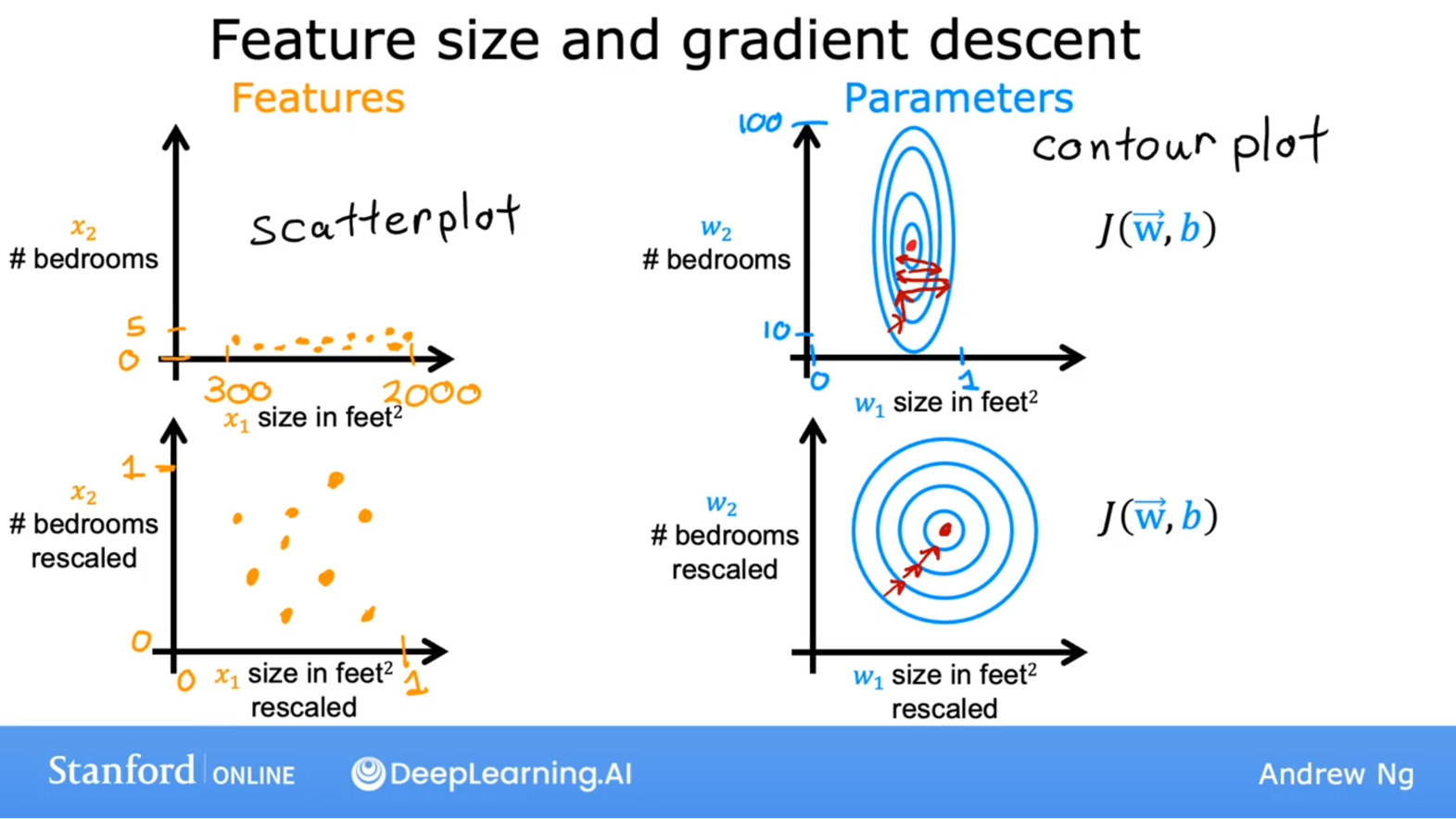
• 均值归一化（mean normalization）：

\[x_j^{(i)} := \frac{x_j^{(i)} - \mu_j}{\max (x_j) - \min (x_j)} \]

其中：\(\vec{x}^{(i)} = (x_1^{(i)}, x_2^{(i)}, ..., x_j^{(i)}, ..., x_n^{(i)})\)， \(\mu_j\) 为所有 \(x_j\) 的平均值（mean），即

\[\mu_j = \frac{1}{n} \sum_{i=1}^{n} x_j^{(i)} \]

• z-score 归一化（z-score normalization）：

\[x_j^{(i)} := \frac{x_j^{(i)} - \mu_j}{\sigma_j} \]

其中：\(\vec{x}^{(i)} = (x_1^{(i)}, x_2^{(i)}, ..., x_j^{(i)}, ..., x_n^{(i)})\)， \(\sigma_j\) 为所有 \(x_j\) 的标准差（Standard Deviation，std），即

\[\mu_j = \sqrt {\frac{1}{n} \sum_{i=1}^{n} [x_j^{(i)} - \mu_j]^2} \]

• 【归一化的问题】训练出的结果 W 和 B，在使用测试集推理时有两种使用方式：
  • 直接使用，此时必须把预测时输入的 X 也做相同规则的归一化。
  • 反归一化为 W，B 的本来值 W_real 和 B_real，推理时输入的 X 不需要改动。
  • 另外，Y 也可以归一化，好处是迭代次数少。如果结果收敛，也可以不归一化，如果不收敛（数值过大），就必须归一化。如果 Y 归一化，对得出来的结果做关于 Y 的反归一化。
• 实现代码：

import numpy as np
import matplotlib.pyplot as plt

# 均值归一化
def mean_normalize_features(X):
    mu = np.mean(X, axis=0) # 计算平均值，矩阵可指定计算行(axis=1)或列(axis=0，此处即特征值)
    X_mean = (X - mu) / (np.max(X, axis=0) - np.min(X, axis=0))
    return X_mean

# z-score 归一化
def zscore_normalize_features(X):
    mu = np.mean(X, axis=0) # 计算平均值，矩阵可指定计算行(axis=1)或列(axis=0，此处即特征值)
    sigma = np.std(X, axis=0) # 计算标准差，矩阵可指定计算行(axis=1)或列(axis=0，此处即特征值)
    X_zscore = (X - sigma) / mu
    return X_zscore

# 计算误差均方函数 J(w,b)
def cost_function(X, y, w, b):
    m = X.shape[0] # 训练集的数据样本数
    cost_sum = 0.0
    for i in range(m):
        f_wb_i = np.dot(w, X[i]) + b
        cost = (f_wb_i - y[i]) ** 2
        cost_sum += cost
    return cost_sum / (2 * m)

# 计算梯度值 dJ/dw, dJ/db
def compute_gradient(X, y, w, b):
    m = X.shape[0] # 训练集的数据样本数（矩阵行数）
    n = X.shape[1] # 每个数据样本的维度（矩阵列数）
    dj_dw = np.zeros((n,))
    dj_db = 0.0
    for i in range(m): # 每个数据样本
        f_wb_i = np.dot(w, X[i]) + b
        for j in range(n): # 每个数据样本的维度
            dj_dw[j] += (f_wb_i - y[i]) * X[i, j]
        dj_db += (f_wb_i - y[i])
    dj_dw = dj_dw / m
    dj_db = dj_db / m
    return dj_dw, dj_db

# 梯度下降算法
def linear_regression(X, y, w, b, learning_rate=0.01, epochs=1000):
    J_history = [] # 记录每次迭代产生的误差值
    for epoch in range(epochs):
        dj_dw, dj_db = compute_gradient(X, y, w, b)
        # w 和 b 需同步更新
        w = w - learning_rate * dj_dw
        b = b - learning_rate * dj_db
        J_history.append(cost_function(X, y, w, b)) # 记录每次迭代产生的误差值
    return w, b, J_history

# 绘制散点图
def draw_scatter(x, y, title):
    plt.xlabel("X-axis", size=15)
    plt.ylabel("Y-axis", size=15)
    plt.title(title, size=20)
    plt.scatter(x, y)

# 打印训练集数据和预测值数据以便对比
def print_contrast(train, prediction, n):
    print("train  prediction")
    for i in range(n):
        print(np.round(train[i], 4), np.round(prediction[i], 4))

# 从这里开始执行
if __name__ == '__main__':
    # 训练集样本
    data = np.loadtxt("./data.txt", delimiter=',', skiprows=1)
    X_train = data[:, :4]  # 训练集的第 0-3 列为 X = (x0, x1, x2, x3)
    y_train = data[:, 4]  # 训练集的第 4 列为 y
    w = np.zeros((X_train.shape[1],))  # 权重
    b = 0.0  # 偏置
    epochs = 1000  # 迭代次数
    learning_rate = 0.01  # 学习率
    J_history = []  # 记录每次迭代产生的误差值

    # Z-score 归一化
    X_norm = zscore_normalize_features(X_train)
    #y_norm = zscore_normalize_features(y_train)
    print(f"X_norm = {np.round(X_norm, 4)}")
    #print(f"y_norm = {np.round(y_norm, 4)}")

    # 线性回归模型的建立
    w, b, J_history = linear_regression(X_norm, y_train, w, b, learning_rate, epochs)
    print(f"result: w = {np.round(w, 4)}, b = {b:0.4f}")  # 打印结果

    # 训练集 y_train 与预测值 y_hat 的对比（这里其实我偷了个懒，训练集当测试集用，以后不要这样做！）
    y_hat = np.zeros(X_train.shape[0])
    for i in range(X_train.shape[0]):
        # 注意，测试集的输入也需要进行归一化！
        y_hat[i] = np.dot(w, X_norm[i]) + b
    print_contrast(y_train, y_hat, y_train.shape[0])

    # 绘制误差值的散点图
    x_axis = list(range(0, epochs))
    draw_scatter(x_axis, J_history, "Cost Function in Every Epoch")
    plt.show()

正则化线性回归（regularization linear regression）

• 正则化的作用：解决过拟合（overfitting）问题（也可通过增加训练样本数据解决）。
• 损失/代价函数（仅需正则化 \(w\)，无需正则化 \(b\)）：

\[\begin{aligned} J(\vec{w}, b) &= \frac{1}{2m} \sum^{m}_{i=1} [f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}]^2 + \frac{\lambda}{2m} \sum^{n}_{j=1} w_j^2 \end{aligned} \]

其中，第一项称为均方误差（mean squared error），第二项称为正则化项（regularization term），使 \(w_j\) 变小。初始设置的 \(\lambda\) 越大，最终得到的 \(w_j\) 越小。

• 梯度下降算法：

\[\begin{aligned} repeat \{ \\ & tmp\_w_1 = w_1 - \alpha \frac{1}{m} \sum^{m}_{i=1} [f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}] x_1^{(i)} + \frac{\lambda}{m} w_1 \\ & tmp\_w_2 = w_2 - \alpha \frac{1}{m} \sum^{m}_{i=1} [f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}] x_2^{(i)} + \frac{\lambda}{m} w_2 \\ & ... \\ & tmp\_w_n = w_n - \alpha \frac{1}{m} \sum^{m}_{i=1} [f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}] x_n^{(i)} + \frac{\lambda}{m} w_n \\ & tmp\_b = b - \alpha \frac{1}{m} \sum^{m}_{i=1} [f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}] \\ & simultaneous \ update \ every \ parameters \\ \} until \ & converge \end{aligned} \]