【算法设计-搜索】回溯法应用举例(3)——排列组合问题
9. 全排列问题(不考虑重复数字)
【描述】什么是全排列?例如,给定一串数字 1,2,3,那么它们的全排列就是:
- 1,2,3
- 1,3,2
- 2,1,3
- 2,3,1
- 3,1,2
- 3,2,1
注意,该问题不考虑有重复数字的情况。
【算法分析】运用回溯的思想。
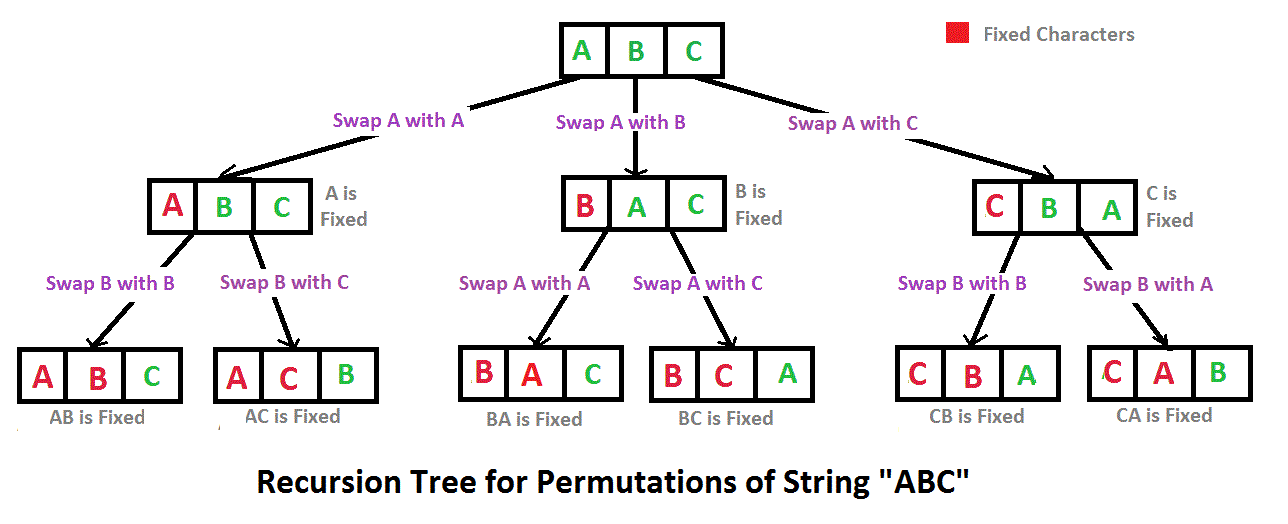
假设有三个元素,初始情况为:
| i=0 | i=1 | i=2 |
|---|---|---|
| 0 | 1 | 2 |
注意:括号内的是元素,i=X 为下标!
- 以 i=0 为基准,分别与后面其他元素交换,先与 i=0 交换(0 1 2)。
- 以 i=1 为基准,分别与后面其他元素交换,先与 i=1 交换(0 1 2)。
- 以 i=2 为基准,分别与后面其他元素交换,先与 i=2 交换(0 1 2)。
- 此时 i=2 已经没有其他元素可以交换了,所以输出序列(0 1 2),然后把 i=2 与 i=2 换回来(0 1 2)。
- 以 i=1 为基准,先把 i=1 与 i=1 换回来(0 1 2),然后继续与后面其他元素交换,与 i=2 交换(0 2 1)。
- 以 i=2 为基准,分别与后面其他元素交换,先与 i=2 交换(0 2 1)。
- 此时 i=2 已经没有其他元素可以交换了,所以输出序列(0 2 1),然后把 i=2 与 i=2 换回来(0 2 1)。
- 此时 i=1 已经没有其他元素可以交换了,把 i=1 与 i=2 换回来(0 1 2)。
- 以 i=1 为基准,分别与后面其他元素交换,先与 i=1 交换(0 1 2)。
- 以 i=0 为基准,先把 i=0 与 i=0 换回来(0 1 2),继续与后面其他元素交换,与 i=1 交换(1 0 2)。
- 以 i=1 为基准,分别与后面其他元素交换,先与 i=1 交换(1 0 2)。
- 以 i=2 为基准,分别与后面其他元素交换,先与 i=2 交换(1 0 2)。
- 此时 i=2 已经没有其他元素可以交换了,所以输出序列(1 0 2),然后把 i=2 与 i=2 换回来(1 0 2)。
- 以 i=1 为基准,先把 i=1 与 i=1 换回来(1 0 2),继续与后面其他元素交换,与 i=2 交换(1 2 0)。
- 以 i=2 为基准,分别与后面其他元素交换,先与 i=2 交换(1 2 0)。
- 此时 i=2 已经没有其他元素可以交换了,所以输出序列(1 2 0),然后把 i=2 与 i=2 换回来(1 2 0)。
- 此时 i=1 已经没有其他元素可以交换了,把 i=1 与 i=2 换回来(1 0 2)。
- 以 i=1 为基准,分别与后面其他元素交换,先与 i=1 交换(1 0 2)。
- 以 i=0 为基准,先把 i=0 与 i=1 换回来(0 1 2),继续与后面其他元素交换,与 i=2 交换(2 1 0)。
- 以 i=1 为基准,分别与后面其他元素交换,先与 i=1 交换(2 1 0)。
- 以 i=2 为基准,分别与后面其他元素交换,先与 i=2 交换(2 1 0)。
- 此时 i=2 已经没有其他元素可以交换了,所以输出序列(2 1 0),然后把 i=2 与 i=2 换回来(2 1 0)。
- 以 i=1 为基准,先把 i=1 与 i=1 换回来(2 1 0),继续与后面其他元素交换,与 i=2 交换(2 0 1)。
- 以 i=2 为基准,分别与后面其他元素交换,先与 i=2 交换(2 0 1)。
- 此时 i=2 已经没有其他元素可以交换了,所以输出序列(2 0 1),然后把 i=2 与 i=2 换回来(2 0 1)。
- 此时 i=1 已经没有其他元素可以交换了,把 i=1 与 i=2 换回来(2 1 0)。
- 以 i=1 为基准,分别与后面其他元素交换,先与 i=1 交换(2 1 0)。
- 此时 i=0 已经没有其他元素可以交换了,执行结束。
假设有 1,2,3,4,则:
- 首先保持 1 不变,对 2,3,4 全排列;
- 保持 2 不变,对 3,4 全排列;
- 保持 3 不变,对 4 全排列,4 的全排列只有一种。得到 1,2,3,4;
- 保持 2 不变,3,4 互换得到 1,2,4,3;
- 以 1,2 打头的排列完成,接下来把 3 换到 2 的位置,继续上面两步的操作。
【算法描述】
void trace (int init){
如果下标 init 超出了数组最大下标
输出方案
否则
循环下标 i: init~数组最大下标
交换 A[init], A[i]
trace(init+1)
交换 A[init], A[i] // 回溯,为下一次交换做准备
}
【题解】
#include <cstdio>
using namespace std;
void swap (int &x, int &y){
int tmp = x;
x = y;
y = tmp;
}
void trace (int A[], int size, int init){
if (init == size){
for (int j = 0; j < size; j++)
printf("%d ", A[j]);
printf("\n");
}
else
for (int i = init; i < size; i++){
swap(A[init], A[i]);
trace(A, size, init+1);
swap(A[init], A[i]);
}
}
int main(){
int n;
int A[10] = {0};
while (scanf("%d", &n) != EOF){
for (int i = 0; i < n; i++)
scanf("%d", &A[i]);
printf("全排列:\n");
trace(A, n, 0);
}
return 0;
}
10. 全排列问题(考虑重复数字)
【描述】什么是考虑重复数字的全排列?例如,给定一串数字 1,2,2,那么它们的全排列就是:
- 1,2,2
- 2,1,2
- 2,2,1
可以看到,我们把重复的情况给剔除了。
【分析】假设有四个元素,初始情况为:
| i=0 | i=1 | i=2 | i=3 |
|---|---|---|---|
| 0 | 1 | 2 | 2 |
i=0 与 i=1、i=2 交换没有问题,当与 i=3 交换时出现了重复。
i=1 与 i=2 交换没有问题,当与 i=3 交换时出现了重复。
再举个例子,假设有五个元素,初始情况为:
| i=0 | i=1 | i=2 | i=3 | i=4 |
|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 2 |
i=0 与 i=1、i=2、i=3 交换没有问题,当与 i=4 交换时出现了重复。
i=1 与 i=2、i=3 交换没有问题,当与 i=4 交换时出现了重复。
i=2 与 i=4 交换时发生了重复。
请观察以上两个例子,为什么会出现重复?因为当与 i=X 交换出现重复的时候,在 i=X 前面一定存在已经换过相同的元素!所以,只需要判断要交换的元素在前面有无重复出现过就够了!
我们以第二个例子说明,i=0 与 i=1、i=2、i=3 交换没有问题,而 i=4 跟之前换过的 i=2 已经重复了。说明区间 i=0~4 有重复元素。
i=1 与 i=2、i=3 交换没有问题,而 i=4 跟之前换过的 i=2 已经重复了。说明区间 i=1~4 有重复元素。
【题解】
bool isSwap (int A[], int init, int end){
for (int i = init; i < end; i++) // 判断基准元素init到要交换元素end的区间内,有没有跟要交换元素end重复的元素
if (A[i] == A[end])
return false;
return true;
}
void trace (int A[], int size, int init){
if (init == size){
for (int j = 0; j < size; j++)
printf("%d ", A[j]);
printf("\n");
}
else
for (int i = init; i < size; i++){
if (isSwap(A, init, i)){ // 判断基准元素init到要交换元素i的区间内,有没有跟要交换元素i重复的元素
swap(A[init], A[i]);
trace(A, size, init+1);
swap(A[init], A[i]);
}
}
}
11. 组合问题(取出数字相同但顺序不同,视为不同组合)
【描述】什么是组合?比如,从 4 个数字(1,2,3,4)中取出 3 个数字,有以下取法:
- 1,2,3
- 1,2,4
- 1,3,2
- 1,3,4
- 1,4,2
- 1,4,3
- 2,1,3
- 2,1,4
- 2,3,1
- 2,3,4
- 2,4,1
- 2,4,3
- 3,1,2
- 3,1,4
- 3,2,1
- 3,2,4
- 3,4,1
- 3,4,2
- 4,1,2
- 4,1,3
- 4,2,1
- 4,2,3
- 4,3,1
- 4,3,2
注意:
- 有些组合取出数字相同但顺序不同,均视为不同组合。
- 不考虑重复数字。
【输入和输出样例】
4 2
1 2 3 4
取出2个的组合:
1 2
1 3
1 4
2 1
2 3
2 4
3 1
3 2
3 4
4 1
4 2
4 3
【分析】运用回溯的思想,每次取出一个数字后就标记该数字已使用过,然后尝试取下一个数字。若该数字已被使用过,则继续尝试下一个数字。
- 使用
result数组记录已取得的数字; - 使用
used数组记录下标对应的元素是否已取出。
【回溯算法描述】
// 取第 cnt 个数字
void trace (int cnt){
如果 cnt == 取出的个数
输出方案
否则
尝试数组 A 的每一个数字
如果该数字没被取出过
取出数字
标记该数字已被取出
trace(cnt+1); // 取第 cnt+1 个数字
放回数字
标记该数字没有被取出
}
【题解】
#include <cstdio>
using namespace std;
#define MAX 10
// A: 原数组, used: 记录下标对应的元素是否已取出, size: 数组A的长度
// num: 取出多少个数字, cnt: 当前取出第几个数字
void trace_dict (int A[], bool used[], int size, int num, int cnt){
static int result[MAX] = {0};
// 若已经取出 num 个数字,则说明已经完成要求,输出方案
if (cnt == num+1){
for (int i = 1; i <= num; i++)
printf("%d ", result[i]);
printf("\n");
return;
}
// 尝试从数组 A 取出每一个数字
for (int i = 0; i < size; i++){
if (!used[i]){ // 如果没有取出该数字
result[cnt] = A[i]; // 取出数字
used[i] = true; // 下标对应的元素已取出
trace_dict(A, used, size, num, cnt+1); // 开始取出第 cnt+1 个数字
result[cnt] = 0; // 放回数字
used[i] = false; // 下标对应的元素未取出
}
}
}
int main(){
int A[MAX] = {0};
bool used[MAX] = {false};
int size, num;
while (scanf("%d%d", &size, &num) != EOF){
for (int i = 0; i < size; i++)
scanf("%d", &A[i]);
printf("取出%d个的组合:\n", num);
trace_dict(A, used, size, num, 1); // 初始为取出第 1 个数字
printf("\n");
}
return 0;
}
12. 组合问题(取出数字相同但顺序不同,视为相同组合)
【描述】什么是组合?比如,从 4 个数字(1,2,3,4)中取出 3 个数字,有以下取法:
- 1,2,3
- 1,2,4
- 1,3,4
- 2,3,4
注意:
- 有些组合取出数字相同但顺序不同,均视为同一组合,因此就这么少了。
- 不考虑重复数字。
【分析】取出下标为第 i 个数字后,在取下一个数字时,只能取区间 [i+1, size-1] 里的数(size 为数组大小),每取一次数都这样操作,就可以避免重复组合了。
【题解】
#include <cstdio>
using namespace std;
#define MAX 10
// A: 原数组, used: 记录下标对应的元素是否已取出, size: 数组A的长度
// num: 取出多少个数字, cnt: 当前取出第几个数字, pos: 取出的位置
void trace(int A[], bool used[], int size, int num, int cnt, int pos){
static int result[MAX] = {0};
// 若已经取出 num 个数字,则说明已经完成要求,输出方案
if (cnt == num+1){
for (int i = 1; i <= num; i++)
printf("%d ", result[i]);
printf("\n");
return;
}
// 尝试从数组 A 的 pos 位置开始取出每一个数字
for (int i = pos; i < size; i++){
if (!used[i]){ // 如果没有取出该数字
result[cnt] = A[i]; // 取出数字
used[i] = true; // 下标对应的元素已取出
trace(A, used, size, num, cnt+1, i+1); // 开始取出第 cnt+1 个数字,从下标为 i+1 开始取数
result[cnt] = 0; // 放回数字
used[i] = false; // 下标对应的元素未取出
}
}
}
int main(){
int A[MAX] = {0};
bool used[MAX] = {false};
int size, num;
while (scanf("%d%d", &size, &num) != EOF){
for (int i = 0; i < size; i++)
scanf("%d", &A[i]);
printf("取出%d个的组合:\n", num);
trace(A, used, size, num, 1, 0); // 初始为取出第 1 个数字,从下标为 0 开始取数
printf("\n");
}
return 0;
}
13. 子集问题(集合代数中的子集定义)
【描述】什么是子集?假设有一集合 {1,2,3,4},求出其子集有:
注意:
- 按照集合定义,有些取出数字相同但顺序不同,均视为同一子集。
- 按照集合定义,子集并不等同于真子集,所以 1,2,3,4 也算子集。
- 不考虑重复数字。
- 空集不用输出。
【分析】一种最简单的想法是将组合问题的程序直接拿过来用,分别输出取出 1 个数、取出 2 个数、取出 3 个数、···的方案。
【题解】
#include <cstdio>
using namespace std;
#define MAX 10
// A: 原数组, used: 记录下标对应的元素是否已取出, size: 数组A的长度
// num: 取出多少个数字, cnt: 当前取出第几个数字, pos: 取出的位置
void trace(int A[], bool used[], int size, int num, int cnt, int pos){
static int result[MAX] = {0};
// 若已经取出 num 个数字,则说明已经完成要求,输出方案
if (cnt == num+1){
printf("{");
for (int i = 1; i <= num; i++){
if (i != num)
printf("%d,", result[i]);
else
printf("%d}", result[i]);
}
printf("\n");
return;
}
// 尝试从数组 A 的 pos 位置开始取出每一个数字
for (int i = pos; i < size; i++){
if (!used[i]){ // 如果没有取出该数字
result[cnt] = A[i]; // 取出数字
used[i] = true; // 下标对应的元素已取出
trace(A, used, size, num, cnt+1, i+1); // 开始取出第 cnt+1 个数字,从下标为 i+1 开始取数
result[cnt] = 0; // 放回数字
used[i] = false; // 下标对应的元素未取出
}
}
}
int main(){
int A[MAX] = {0};
bool used[MAX] = {false};
int size;
while (scanf("%d", &size) != EOF){
for (int i = 0; i < size; i++)
scanf("%d", &A[i]);
for (int i = 1; i <= size; i++){
printf("取出%d个的子集:\n", i);
trace(A, used, size, i, 1, 0); // 目标是取出 i 个数字,初始为取出第 1 个数字,从下标为 0 开始取数
}
printf("\n");
}
return 0;
}
【输入和输出】
4
1 2 3 4
取出1个的子集:
{1}
{2}
{3}
{4}
取出2个的子集:
{1,2}
{1,3}
{1,4}
{2,3}
{2,4}
{3,4}
取出3个的子集:
{1,2,3}
{1,2,4}
{1,3,4}
{2,3,4}
取出4个的子集:
{1,2,3,4}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号