【数据结构-树】哈夫曼树及其应用

目录

• 1 哈夫曼树的构造
• 2 哈夫曼树的应用——哈夫曼编码
• 3 相关例子
• 4 求哈夫曼树的 WPL 代码

1 哈夫曼树的构造

• 将 n 个结点作为 n 棵仅含一个节点的二叉树，构成森林 F
• 在 F 中选取两棵权值最小的二叉树，作为新结点的左右子树，并将新结点的权值置为左、右子树的根结点的权值之和
• 将新结点的二叉树加入 F 中，同时删去原来两棵选取出来的二叉树
• 重复以上步骤，直到 F 中只剩一棵二叉树

【哈夫曼树的性质】

• 构造过程中一共新建了 n-1 个结点
• 总结点数为 2n-1
• 不存在度为 1 的结点
• 哈夫曼树并不唯一
• 哈夫曼树的 WPL 一定相同且最优

2 哈夫曼树的应用——哈夫曼编码

哈夫曼编码的译码过程（从编码到字符）：

• 从左至右依次扫描字符串的各位
• 从哈夫曼树根开始，根据串中当前字符，沿当前结点的左指针或右指针，一直移动到叶结点为止，输出叶结点中保存的字符
• 一直重复这个过程，直到扫描到字符串结束为止

3 相关例子

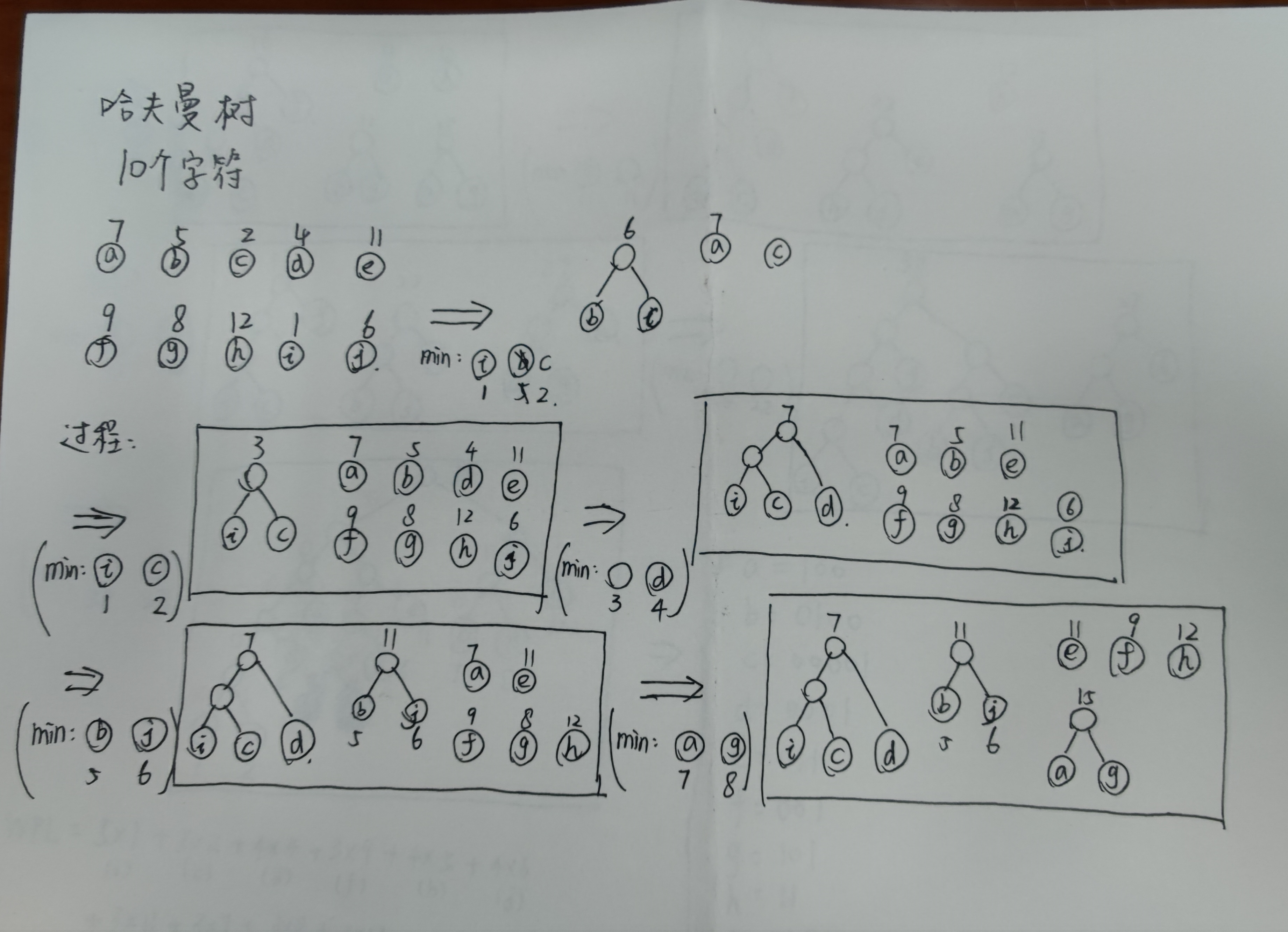
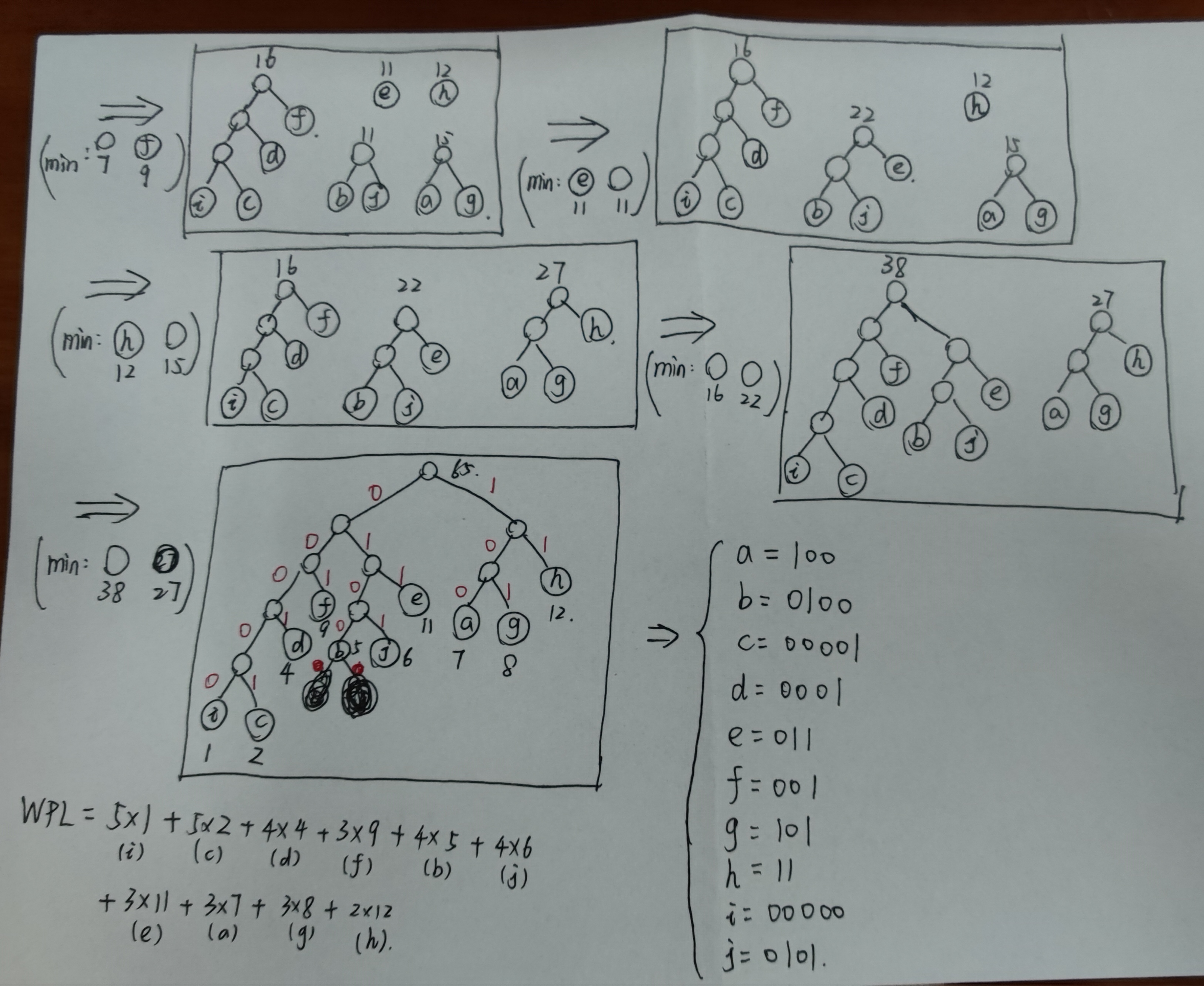
• WPL：树的所有叶结点的带权路径长度之和
• WPL = (W1L1 + W2L2 + W3L3 + ... + WnLn)，N 个权值W_i (i=1,2,...n) 构成一棵有 N 个叶结点的二叉树，相应的叶结点的路径长度为 L_i (i=1,2,...n)

4 求哈夫曼树的 WPL 代码

使用优先队列（总是最大或最小元素出队，其原理为堆排序），每次取出队列中两个最小元素的结点，它们加起来为新结点的权值，又将新结点放回优先队列中，如此反复，直到队列中仅剩一个结点，即一棵哈夫曼树构建完毕。

#include <string>
#include <queue>
using namespace std;

int main(){
	int n, x, weight;
	
	while (scanf("%d", &n) != EOF){
		weight = 0;
		priority_queue <int, vector<int>, greater<int> > q;
		
		for (int i = 0; i < n; i++){
			scanf("%d", &x);
			q.push(x);
		}
		
		while (q.size() > 1){
			int tmp_a = q.top();
			q.pop();
			int tmp_b = q.top();
			q.pop();
			weight += tmp_a + tmp_b;
			q.push(tmp_a + tmp_b);
		}
		
		printf("%d\n", weight);
	}
	
	return 0;
}