【数据结构-树】并查集的基本操作

目录

• 1 数据结构定义
• 2 初始化
• 3 查找操作
• 4 并操作

1 数据结构定义

#define MAX 50
int UFSets[MAX]; // 并查集

2 初始化

// 参数：并查集 S
void Init (int S[]){
    int i;
    for (i = 0; i < MAX; i++)
        S[i] = -1;
}

【注】根结点可用来保存该子集合的元素个数（负数表示）。

3 查找操作

• 寻找包含 x 的树根：

// 参数：并查集 S，索引/下标 x
int Find (int S[], int x){
    while (S[x] >= 0)
        x = S[x];
    return x;
}

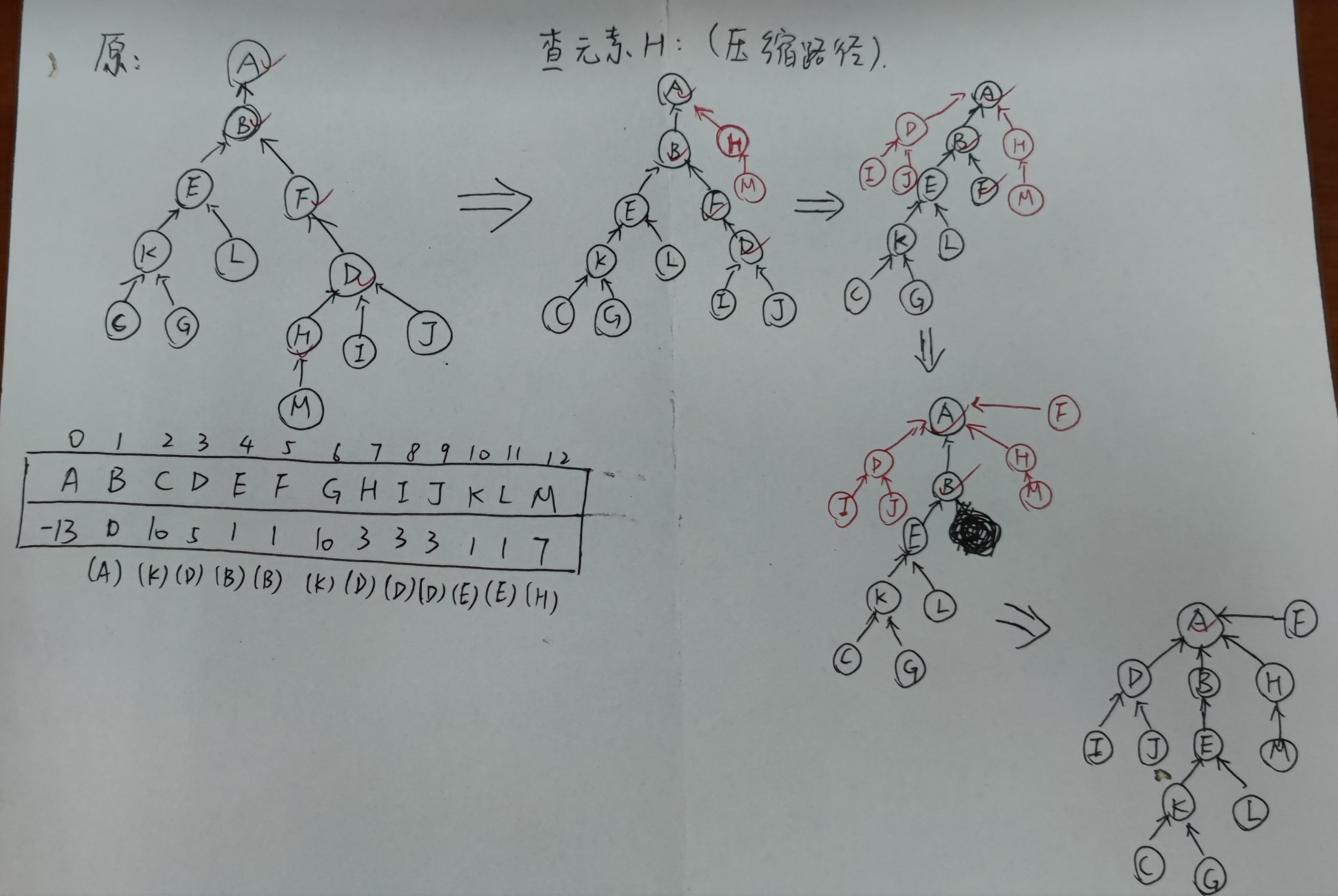
• 压缩路径：先找到根结点，再将查找路径上所有结点都挂在根结点上

// 参数：并查集 S，索引/下标 x
int Find (int S[], int x){
    int root = x;
    
    // 寻根
    while (S[root] >= 0)
        root = S[root];
        
    // 压缩路径
    while (x != root){ 
        int t = S[x]; // t 暂时保存 x 的双亲结点（不一定是根结点！）
        S[x] = root; // x 直接挂在根结点下
        x = t; // x 更新为双亲结点
    }
    
    return root;
}

• 压缩路径：一边查找一边压缩路径，将查找路径上所有结点都挂在根结点上（递归写法）

// 参数：并查集 S，索引/下标 x
int Find (int S[], int x){
    if (S[x] < 0) // 如果就是根结点
        return x;
    else{ // 如果不是根结点，一边查找一边压缩路径
        S[x] = Find(S[x]); // 找到其根结点，将双亲结点更新为其根结点
        return S[x];
    }
}

4 并操作

• 把集合 S 中的子集合 Root2 并入子集合 Root1：

void Union (int S[], int Root1, int Root2){
    if (Root2 != Root1) // Root2 和 Root1 必须是不同的两个集合
        S[Root2] = Root1;
}

• 把集合 S 中，包含元素 y 的子集合 Root2 并入包含元素 x 的子集合 Root1：

void Union (int S[], int x, int y){
    S[Find(y)] = Find(x);
}