【数据结构-图】有向无环图的应用
目录
1 拓扑序列——AOV 网
1.1 手工运算拓扑序列
对 AOV 网进行拓扑排序的步骤：
- 从 AOV 网中选择一个没有前驱（即入度为 0）的顶点输出；
- 从网中删除该顶点和所有以它为起点的有向边；
- 重复前面两个步骤，直到当前 AOV 网为空；
- 若 AOV 网中不存在无前驱的顶点，则说明有向图中必然存在环。
1.2 手工运算逆拓扑序列
对 AOV 网进行拓扑排序的步骤：
- 从 AOV 网中选择一个没有后继（即出度为 0）的顶点输出；
- 从网中删除该顶点和所有以它为终点的有向边；
- 重复前面两个步骤，直到当前 AOV 网为空；
1.3 代码实现拓扑序列
/* 存储结构：邻接表 */
Stack S; // 存储入度为 0 的顶点编号
int indegree[MAX_VERTEX_NUM]; // 当前每个顶点的入度
bool TopoSort (Graph G){
int count = 0; // 记录当前已经输出的顶点个数
InitStack(S);
for (int i = 0; i < G.vexnum; i++){
if (inDegree[i] == 0) // 将所有入度为 0 的顶点，进栈
Push(S, i);
}
while (!IsEmpty(S)){ // 若栈非空，则说明存在入度为 0 的顶点
Pop(S, i); // 栈顶元素顶点 i 出栈
print[count] = i; // 输出顶点 i
count++;
// 遍历顶点 i 的边表，即遍历顶点 i 的所有出度顶点
for (Arcnode *p = G.vertices[i].firstarc; p != NULL; p = p->nextarc){
v = p->adjvex; // 获取出度顶点编号
indegree[v]--; // 出度顶点的入度减 1
if (inDegree[i] == 0) // 若出度顶点的入度为 0，进栈
Push(S, i);
}
}
if (count < G.vexnum) // 排序失败，说明有回路
return false;
else // 排序成功
return true;
}
1.4 代码实现逆拓扑序列（DFS 算法）
bool visited[MAX_VERTEX_NUM]; // 标记顶点的访问情况
void DFSTraverse (Graph G){
for (v = 0; v < G.vexnum; v++){
visited[v] = FALSE; // 初始化各顶点的访问情况为未访问
}
for (v = 0; v < G.vexnum; v++){
if (visited[v] == FALSE)
DFS(G, v);
}
}
void DFS (Graph G, int v){
visited[v] = TRUE; // 设置该结点为已访问过
// 依次访问 v 的邻接点
for (int w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)){
if (visited[w] == FALSE) // 若顶点 w 尚未访问
DFS(G, w);
}
print(v); // 输出顶点（在顶点退栈前访问顶点）
}
2 关键路径——AOE 网
- 关键路径：从源点到汇点的所有路径中，具有最大长度的路径（因此可以直接手算关键路径）
- 关键活动：关键路径上的所有活动都是关键活动
- 可通过加快关键活动来缩短工期，但不可任意缩短关键活动，因为一旦缩短到一定程度，该关键活动就可能变成非关键活动
- 关键路径可能不唯一，只有加快所有关键路径上的关键活动才能缩短工期
以下面有向图为例：
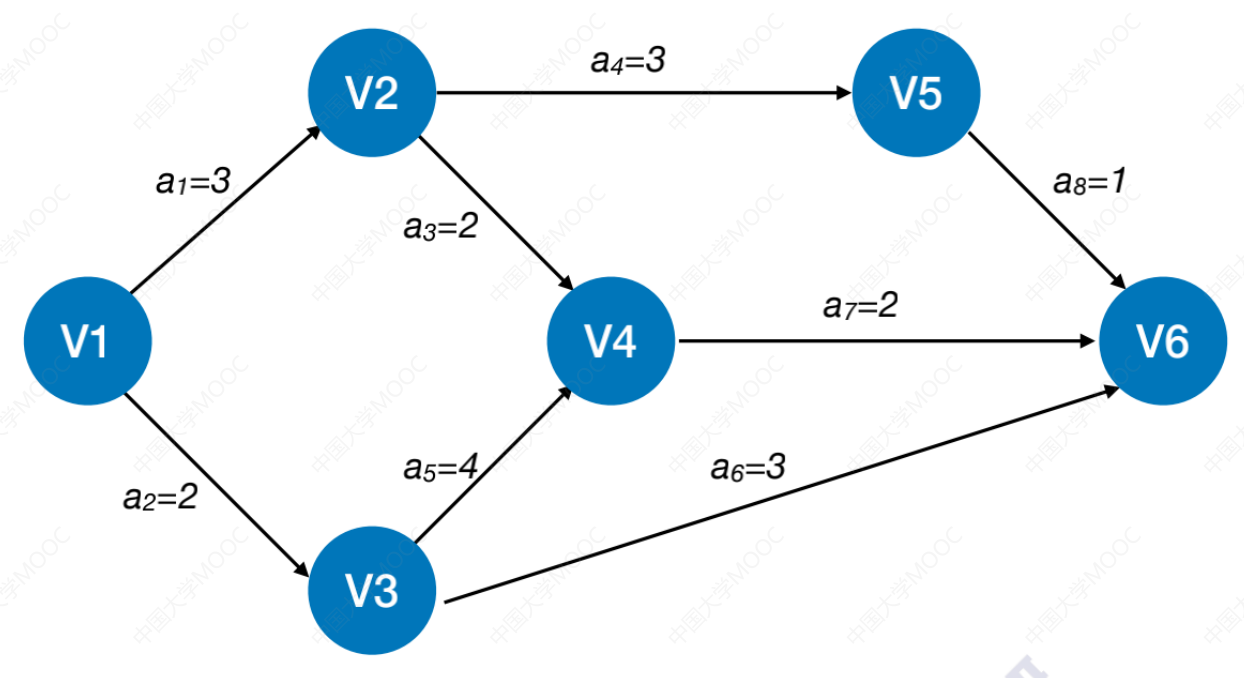
2.1 所有事件的最早发生时间 ve(vk)
【注】“事件”即顶点。
【公式】所有事件的最早发生时间：
ve(起点) = 0ve(顶点) = max{ve(前驱顶点) + 边权值}
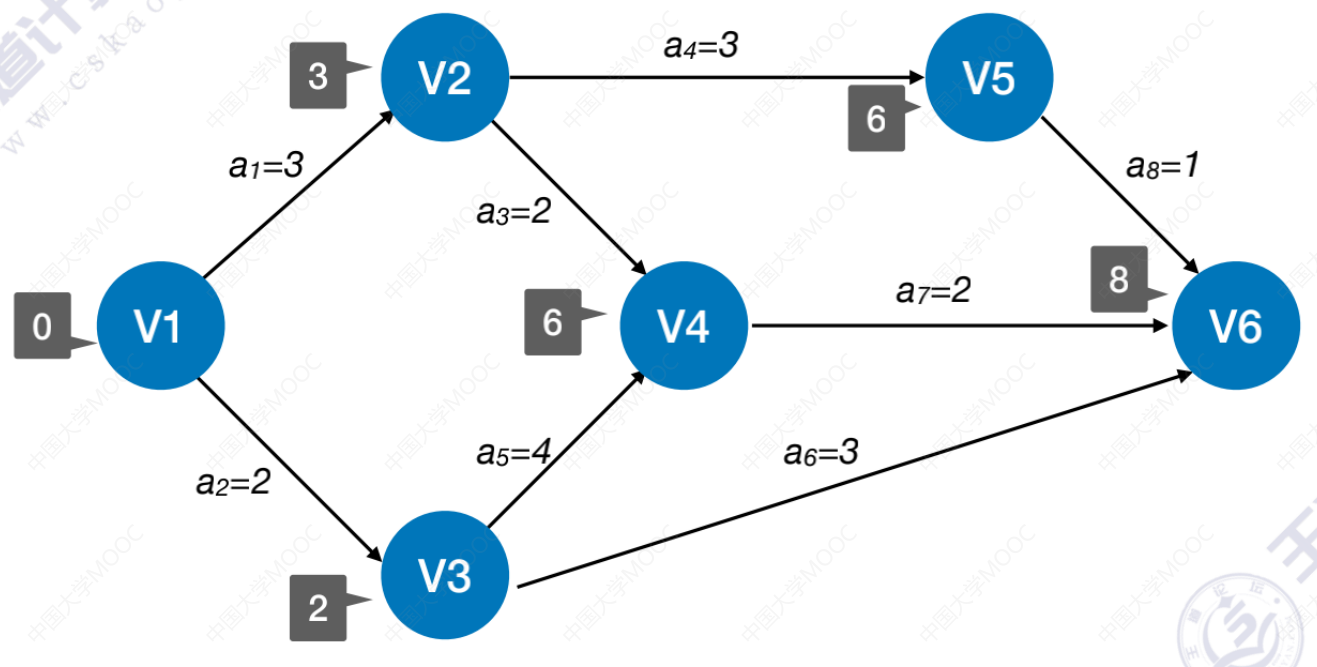
- ve(1) = 0
- ve(2) = 3
- ve(3) = 2
- ve(4) = max {ve(2) + 2, ve(3) + 4} = max {5, 6} = 6
- ve(5) = ve(2) + 3 = 6
- ve(6) = max {ve(3) + 3, ve(4) + 2, ve(5) + 1} = max {5, 8, 7} = 8
2.2 所有事件的最迟发生时间 vl(vk)
【注】“事件”即顶点。
【公式】所有事件的最迟发生时间：
vl(终点) = 关键路径长度vl(顶点) = min{ve(后继顶点) - 边权值}
- vl(6) = 8
- vl(5) = vl(6) - 1 = 7
- vl(4) = vl(6) - 2 = 6
- vl(3) = min {vl(6) - 3, vl(4) - 4} = min {5, 2} = 2
- vl(2) = min {vl(5) - 3, vl(4) - 2} = min {4, 4} = 4
- vl(1) = min {vl(3) - 2, vl(2) - 3} = min {0, 1} = 0
2.3 所有活动的最早发生时间 e(ai)
【注】“活动”即边。
【公式】所有活动的最早发生时间：
e(边) = ve(边起点)
- e(1) = 0
- e(2) = 0
- e(3) = 3
- e(4) = 3
- e(5) = 2
- e(6) = 2
- e(7) = 6
- e(8) = 6
2.4 所有活动的最迟发生时间 l(ai)
【注】“活动”即边。
【公式】所有活动的最早发生时间：
l(边) = vl(边终点) - 该边权值
- l(8) = vl(6) - 1 = 7
- l(7) = vl(6) - 2 = 6
- l(6) = vl(6) - 3 = 5
- l(5) = vl(4) - 4 = 2
- l(4) = vl(5) - 3 = 4
- l(3) = vl(4) - 2 = 4
- l(2) = vl(3) - 2 = 0
- l(1) = vl(2) - 3 = 1
2.5 所有活动的时间余量 d(ai)
【注】“活动”即边。
【公式】所有活动的最早发生时间：
d(边) = l(边) - e(边)
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | |
|---|---|---|---|---|---|---|---|---|
| l(ai) | 1 | 0 | 4 | 4 | 2 | 5 | 6 | 7 |
| e(ai) | 0 | 0 | 3 | 3 | 2 | 2 | 6 | 6 |
| d(ai) | 1 | 0 | 1 | 1 | 0 | 3 | 0 | 1 |
- d(ai)=0 的活动即是关键活动，由关键活动即可得关键路径
3 有向无环图（DAG）描述表达式
将一个表达式转换为 DAG 的步骤：
- 把各个操作数不重复地排成一排；
- 标出表达式中各个运算符的运算顺序；
- 按顺序往图中加入运算符，注意“分层”；
- 从 DAG 的最底层开始，向上逐层检查同层的运算符是否可以合并。只要发现某几个运算符的出边指向的目标都相同，那么这几个运算符就可以合并。
