算法提高课
第一章动态规划
数字三角形模型
摘花生
分析:数字三角形这一类问题比较号列出状态方程,因此常规题难度并不大。本题是要求出最大值,所以f[N][N]可以初始化为0。
f[i][j]可以由两种状态转化而来:
- 由左边而来。
f[i-1][j] - 由上边而来。
f[i][j-1]
因此取二者最大值(本题不是求方案数)。
状态方程为:
代码:
/*
qwq!
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <map>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <cmath>
#include <unordered_map>
using namespace std;
#define pb push_back
#define pu push
#define fi first
#define se second
#define LL long long
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 110;
int w[N][N];
int f[N][N];
int main() {
ios::sync_with_stdio(false);
int t; cin >> t;
while(t--) {
int n, m; cin >> n >> m;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cin >> w[i][j];
memset(f, 0, sizeof f);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++) {
w[i][j] += max(w[i-1][j], w[i][j-1]);
}
cout << w[n][m] << endl;
}
return 0;
}
最低通行费用
分析:本题与上一题摘花生有所不同,本题是求最小值。因此我们在初始化f[N][N]时需要初始化为正无穷。另外题目本身说了时间不超过(2*N-1)这提示我们只能按右下方向行走。
那么状态方程也和摘花生一样,不过本题是求最小值,不能和上题一样直接加。
代码:
/*
qwq!
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <map>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <cmath>
#include <unordered_map>
using namespace std;
#define pb push_back
#define pu push
#define fi first
#define se second
#define LL long long
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 110;
int w[N][N];
int f[N][N];
int main() {
ios::sync_with_stdio(false);
int n; cin >> n;
memset(f, 0x3f, sizeof f);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
cin >> w[i][j];
f[1][1] = w[1][1];
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(i > 1) f[i][j] = min(f[i][j], f[i-1][j] + w[i][j]);
if(j > 1) f[i][j] = min(f[i][j], f[i][j-1] + w[i][j]);
}
}
cout << f[n][n] << endl;
return 0;
}
方格取数
分析:跟摘花生不一样,这题是要走两遍,并且一个方格只能取一次数。当两次走到同一个格子时,会有他们的起点相同,终点也相同,所以说曼哈顿距离也就相同了。
不妨设曼哈顿距离为k,这样的话,我们只需要知道k和i1、i2就可知j1、j2。设状态方程为:f[k][i1][i2]。
两个小朋友有四种情况:
首先 设一个变量t 如果两次没有走到同一个点 t 就等两次走到方格的数字之和,否则就是相同方格的数字。
- 下右:
f[k][i1][i2] = max(f[k][i1][i2],f[k-1][i1-1][i2]+t) - 下下:
f[k][i1][i2] = max(f[k][i1][i2],f[k-1][i1-1][i2-1]+t) - 右下:
f[k][i1][i2] = max(f[k][i1][i2],f[k-1][i1][i2-1]+t) - 右右:
f[k][i1][i2] = max(f[k][i1][i2],f[k-1][i1][i2]+t)
因此得出f[k][i1][i2]的状态方程;
代码:
/*
qwq!
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <map>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <cmath>
#include <unordered_map>
using namespace std;
#define pb push_back
#define pu push
#define fi first
#define se second
#define LL long long
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 20;
int w[N][N];
int f[2 * N][N][N];
int main() {
ios::sync_with_stdio(false);
int n; cin >> n;
int a, b, c;
while(cin >> a >> b >> c, a || b || c) w[a][b] = c;
for(int k = 2; k <= n + n; k++)
for(int i1 = 1; i1 <= n; i1++)
for(int i2 = 1; i2 <= n; i2++) {
int t = w[i1][k-i1];
if(i1 != i2) t += w[i2][k-i2];
// 下下
f[k][i1][i2] = max(f[k][i1][i2], f[k-1][i1-1][i2-1] + t);
// 下右
f[k][i1][i2] = max(f[k][i1][i2], f[k-1][i1-1][i2] + t);
// 右下
f[k][i1][i2] = max(f[k][i1][i2], f[k-1][i1][i2-1] + t);
// 右右
f[k][i1][i2] = max(f[k][i1][i2], f[k-1][i1][i2] + t);
}
cout << f[2 * n][n][n] << endl;
return 0;
}
传纸条
分析:这题和方格取数是一样的。
代码:
/*
qwq!
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <map>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <cmath>
#include <unordered_map>
using namespace std;
#define pb push_back
#define pu push
#define fi first
#define se second
#define LL long long
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 60;
int w[N][N];
int f[N*2][N][N];
int main() {
ios::sync_with_stdio(false);
int n, m; cin >> n >> m;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cin >> w[i][j];
for(int k = 2; k <= n + m; k++)
for(int i1 = max(1, k - m); i1 <= min(k - 1, n); i1++)
for(int i2 = max(1, k - m); i2 <= min(k - 1, n); i2++) {
int t = w[i1][k-i1];
if(i1 != i2) t += w[i2][k-i2];
for(int i = 0; i < 2; i++)
for(int j = 0; j < 2; j++)
f[k][i1][i2] = max(f[k][i1][i2], f[k-1][i1-i][i2-j] + t);
}
cout << f[n + m][n][n] << endl;
return 0;
}
最长上升子序列模型(LIS模型)
怪盗基德的滑翔翼
分析: 分别向左、向右看最长下降子序列。取最大值。
代码:
#include <iostream>
using namespace std;
const int N = 110;
int h[N];
int L[N], R[N];
int main() {
int t; cin >> t;
while(t--) {
int n; cin >> n;
for(int i = 0; i < n; i++) {
cin >> h[i];
L[i] = R[i] = 1;
for(int j = 0; j < i; j++) {
if(h[i] > h[j]) L[i] = max(L[i], L[j] + 1);
else R[i] = max(R[i], R[j] + 1);
}
}
int ans = 0;
for(int i = 0; i < n; i++) ans = max(ans, max(R[i], L[i]));
cout << ans << endl;
}
return 0;
}
登山
分析:题目刚开始没读明白。实质上就是求一个先严格上升后严格下降的子序列的最大长度。可以先顺着求一边最长上升子序列,再倒着求一边最长上升子序列。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int h[N];
int L[N], R[N];
int main() {
int n; cin >> n;
for(int i = 0; i < n; i++) cin >> h[i];
for(int i = 0; i < n; i++) {
L[i] = 1;
for(int j = 0; j < i; j++)
if(h[i] > h[j]) L[i] = max(L[i], L[j] + 1);
}
for(int i = n - 1; i >= 0; i--) {
R[i] = 1;
for(int j = n - 1; j > i; j--)
if(h[i] > h[j]) R[i] = max(R[i], R[j] + 1);
}
int ans = 0;
for(int i = 0; i < n; i++) ans = max(ans, L[i] + R[i] - 1);
cout << ans << endl;
return 0;
}
合唱队形
分析: 跟上题一模一样。 还更明显!
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int h[N];
int R[N], L[N];
int main() {
int n; cin >> n;
for(int i = 0; i < n; i++) cin >> h[i];
for(int i = 0; i < n; i++) {
L[i] = 1;
for(int j = 0; j < i; j++)
if(h[i] > h[j]) L[i] = max(L[i], L[j] + 1);
}
for(int i = n - 1; i >= 0; i--) {
R[i] = 1;
for(int j = n - 1; j > i; j--)
if(h[i] > h[j]) R[i] = max(R[i], R[j] + 1);
}
int ans = 0;
for(int i = 0; i < n; i++) ans = max(ans, R[i] + L[i] - 1);
cout << n - ans << endl;
return 0;
}
友好城市
分析:对于任意一边来说,固定一边,如果要求不相交,那么另外一边所连的点一定是单调递增的。因为固定的点一定是从1走到n,如果要求与另外一边相连的线不相交,肯定是另外一边也是递增的。所以说只要先按一边排序, 然后求另外一边的单调上升子序列就行了。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5010;
pair<int,int> w[N];
int f[N];
int main() {
int n; cin >> n;
for(int i = 0; i < n; i++) cin >> w[i].first >> w[i].second;
sort(w, w + n);
for(int i = 0; i < n; i++) {
f[i] = 1;
for(int j = 0; j < i; j++) {
if(w[i].second > w[j].second) f[i] = max(f[i], f[j] + 1);
}
}
int ans = 0;
for(int i = 0; i < n; i++) ans = max(ans, f[i]);
cout << ans << endl;
return 0;
}
最大上升子序列和
分析:定义f[i]为以w[i]结尾的最大上升子序列和。则可以得出f[i]的状态转移方程:
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N];
int w[N];
int main() {
int n; cin >> n;
for(int i = 0; i < n; i++) cin >> w[i];
for(int i = 0; i < n; i++) {
f[i] = w[i];
for(int j = 0; j < i; j++) {
if(w[i] > w[j]) f[i] = max(f[i], f[j] + w[i]);
}
}
int ans = 0;
for(int i = 0; i < n; i++) ans = max(ans, f[i]);
cout << ans << endl;
return 0;
}
拦截导弹
分析:先求最长上升子序列,然后用一个数组来存储以w[i]结尾的子序列,可以得到该数组一定是单调递增的。根据贪心的思想,末尾一定是越大越好,这样才可以接更多的数。所以找第一个小于等于w[i]的数,替换即可。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 30010;
int f[N], w[N], cnt[N];
int main() {
int n = 0;
while(cin >> w[n]) n++;
for(int i = 0; i < n; i++) {
f[i] = 1;
for(int j = 0; j < i; j++) {
if(w[i] <= w[j]) f[i] = max(f[i], f[j] + 1);
}
}
int ans = 0;
for(int i = 0; i < n; i++) ans = max(ans, f[i]);
cout << ans << endl;
int k = 0;
for(int i = 0; i < n; i++) {
int t = 0;
while(t < k && w[i] > cnt[t]) t++;
if(t >= k) k++;
cnt[t] = w[i];
}
cout << k << endl;
return 0;
}
还可以对其进行二分优化,因为数组具有单调性:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 30010;
int w[N];
int f[N];
int cnt[N];
int main() {
int n = 0;
while(cin >> w[n]) n++;
int len = 0, k = 0;
for(int i = 0; i < n; i++) {
int l = 0, r = len;
while(l < r) {
int mid = l + r + 1 >> 1;
if(f[mid] >= w[i]) l = mid;
else r = mid - 1;
}
len = max(len, r + 1);
f[r + 1] = w[i];
l = 0, r = k;
while(l < r) {
int mid = l + r + 1 >> 1;
if(cnt[mid] < w[i]) l = mid;
else r = mid - 1;
}
k = max(k, r + 1);
cnt[r + 1] = w[i];
}
cout << len << endl << k << endl;
return 0;
}
导弹防御系统
分析:(DFS,迭代加深,剪枝,贪心)
为了能遍历所有情况,我们首先考虑搜索顺序是什么。
搜索顺序分为两个阶段:
- 从前往后枚举每颗导弹属于某个上升子序列,还是下降子序列;
- 如果属于上升子序列,则枚举属于哪个上升子序列(包括新开一个上升子序列);如果属于下降子序列,可以类似处理。
因此可以仿照AcWing 896. 最长上升子序列 II,分别记录当前每个上升子序列的末尾数up[],和下降子序列的末尾数down[]。这样在枚举时可以快速判断当前数是否可以接在某个序列的后面。
注意这里的记录方式和上一题稍有不同: - 这里是记录每个子序列末尾的数;
- 上一题是记录每种长度的子序列的末尾最小值。
此时搜索空间仍然很大,因此该如何剪枝呢?
对于第二阶段的枚举,我们可以仿照上一题的贪心方式,对于上升子序列而言,我们将当前数接在最大的数后面,一定不会比接在其他数列后面更差。
这是因为处理完当前数后,一定出现一个以当前数结尾的子序列,这是固定不变的,那么此时其他子序列的末尾数越小越好。
注意到按照这种贪心思路,up[]数组和down[]数组一定是单调的,因此在遍历时找到第一个满足的序列后就可以直接break了。
最后还需要考虑如何求最小值。因为DFS和BFS不同,第一次搜索到的节点,不一定是步数最短的节点,所以需要进行额外处理。
一般有两种处理方式:
- 记录全局最小值,不断更新;
- 迭代加深。一般平均答案深度较低时可以采用这种方式。
时间复杂度
每个数在第一搜索阶段有两种选择,在第二搜索阶段只有一种选择,但遍历up[]和down[]数组需要 O(n) 的计算量,因此总时间复杂度是 。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 60;
int up[N], down[N], w[N];
int n;
int ans;
void dfs(int u, int su, int sd) {
if(su + sd >= ans) {
return;
}
if(u == n) {
ans = min(ans, su + sd);
}
int k = 0;
while(k < su && w[u] <= up[k]) k++;
if(k < su) {
int t = up[k];
up[k] = w[u];
dfs(u + 1, su, sd);
up[k] = t;
}else {
up[k] = w[u];
dfs(u + 1, su + 1, sd);
}
k = 0;
while(k < sd && w[u] >= down[k]) k++;
if(k < sd) {
int t = down[k];
down[k] = w[u];
dfs(u + 1, su, sd);
down[k] = t;
}else {
down[k] = w[u];
dfs(u + 1, su, sd + 1);
}
}
int main() {
while(cin >> n, n) {
for(int i = 0; i < n; i++) cin >> w[i];
ans = n;
dfs(0, 0, 0);
cout << ans << endl;
}
}
最长公共上升子序列
分析:(DP,线性DP,前缀和)
这道题目是AcWing 895. 最长上升子序列和AcWing 897. 最长公共子序列的结合版,在状态表示和状态计算上都是融合了这两道题目的方法。
状态表示:
f[i][j]代表所有a[1 ~ i]和b[1 ~ j]中以b[j]结尾的公共上升子序列的集合;f[i][j]的值等于该集合的子序列中长度的最大值;
状态计算(对应集合划分):
首先依据公共子序列中是否包含a[i],将f[i][j]所代表的集合划分成两个不重不漏的子集:- 不包含
a[i]的子集,最大值是f[i - 1][j]; - 包含
a[i]的子集,将这个子集继续划分,依据是子序列的倒数第二个元素在b[]中是哪个数:- 子序列只包含
b[j]一个数,长度是1; - 子序列的倒数第二个数是
b[1]的集合,最大长度是f[i - 1][1] + 1; - ...
- 子序列的倒数第二个数是
b[j - 1]的集合,最大长度是f[i - 1][j - 1] + 1;
如果直接按上述思路实现,需要三重循环:
- 子序列只包含
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= n; j ++ )
{
f[i][j] = f[i - 1][j];
if (a[i] == b[j])
{
int maxv = 1;
for (int k = 1; k < j; k ++ )
if (a[i] > b[k])
maxv = max(maxv, f[i - 1][k] + 1);
f[i][j] = max(f[i][j], maxv);
}
}
}
然后我们发现每次循环求得的maxv是满足a[i] > b[k]的f[i - 1][k] + 1的前缀最大值。
因此可以直接将maxv提到第一层循环外面,减少重复计算,此时只剩下两重循环。
最终答案枚举子序列结尾取最大值即可。
时间复杂度
代码中一共两重循环,因此时间复杂度是 。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 3010;
int f[N][N];
int a[N], b[N];
int main() {
int n; cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i <= n; i++) cin >> b[i];
for(int i = 1; i <= n; i++) {
int maxv = 1;
for(int j = 1; j <= n; j++) {
f[i][j] = f[i-1][j];
if(a[i] > b[j]) maxv = max(maxv, f[i-1][j] + 1);
if(a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
}
}
int ans = 0;
for(int i = 1; i <= n; i++) ans = max(ans, f[n][i]);
cout << ans << endl;
return 0;
}
背包模型
采药
分析: 裸的01背包问题直接写。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int w[N], v[N];
int f[N];
int main() {
int n, m; cin >> m >> n;
for(int i = 0; i < n; i++) cin >> v[i] >> w[i];
for(int i = 0; i < n; i++) {
for(int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
cout << f[m] << endl;
return 0;
}
装箱问题
分析:其实可以理解为价值也为体积大小,这样就又可以套01背包问题的板子了。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20010;
int f[N];
int main() {
int m, n; cin >> m >> n;
for(int i = 0; i < n; i++) {
int v; cin >> v;
for(int j = m; j >= v; j--)
f[j] = max(f[j], f[j-v] + v);
}
cout << m - f[m] << endl;
return 0;
}
宠物小精灵之收服
分析:这题很有意思!我就引用墨染空大佬的题解吧!
体积与价值选择问题效率对比
在背包问题中,体积w与价值v是可以互逆的!
可以将表示为体积为能装的最大价值,
也可以将表示为价值为所需的最小体积。
两者等价,我们只需要选择范围较小的那维作为体积就可以了!
这直接影响到时空复杂度。
这题就是个案例。
- 算法1
(体力、精灵球数为费用、精灵数为价值)
表示为体力为,精灵球数为所收集到的最大精灵。
时间复杂度
差不多是的级别。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N][N];
int main() {
int n, m, k; cin >> n >> m >> k;
int w, v;
for(int i = 0; i < k; i++) {
cin >> w >> v;
for(int j = m; j >= v; j--)
for(int t = n; t >= w; t--) {
f[j][t] = max(f[j][t], f[j-v][t-w] + 1);
}
}
int res = 0, ans = 0;
for(int i = 0; i < m; i++) {
if(ans < f[i][n]) {
ans = f[i][n];
res = i;
}
}
cout << f[m-1][n] << ' ' << m - res << endl;
return 0;
}
- 算法2
发现很小,于是就…
(体力、精灵数为费用,精灵球数为价值)
表示体力为 i, 收集了j个精灵用的最小的精灵球数量
时间复杂度
大概是的级别。
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1005, M = 505, S = 105;
const int INF = 0x3f3f3f3f;
int n, m, K, f[M][S];
/*
f[i][j] 表示体力为 i, 收集了 j 个精灵 用的最小的精灵球数量
*/
int main() {
memset(f, 0x3f, sizeof f);
scanf("%d%d%d", &n, &m, &K);
f[0][0] = 0;
for (int i = 1, c, d; i <= K; i++) {
scanf("%d%d", &c, &d);
for (int j = m; j >= d; j--)
for (int k = K; k >= 1; k--)
if(f[j - d][k - 1] + c <= n)
f[j][k] = min(f[j][k], f[j - d][k - 1] + c);
}
for (int k = K; ~k; k--) {
int p = INF;
for (int j = 0; j < m; j++) {
if(f[j][k] != INF && j < p)
p = j;
}
if(p != INF) { printf("%d %d\n", k, m - p); return 0; }
}
return 0;
}
作者:墨染空
链接:https://www.acwing.com/solution/content/4640/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
数字组合
分析:设f[i][j]表示前i个数和为j的方案数。
则根据01背包问题的思路,可分为:
- 包含第
i个数 - 不包含第
i个数
则f[i][j]的状态转移方程可表示为:
再降维。
对了, 很多求方案的问题中,都会设置f[0] = 1等值,意为当和为0是也是一种情况。
代码:
#include <iostream>
using namespace std;
const int N = 10010;
int w[N], f[N];
int main() {
int n, m; cin >> n >> m;
for(int i = 0; i < n; i++) cin >> w[i];
f[0] = 1;
for(int i = 0; i < n; i++) {
for(int j = m; j >= w[i]; j--)
f[j] += f[j-w[i]];
}
cout << f[m] << endl;
return 0;
}
买书
分析:完全背包问题 设f[i][j]表示:前i件物品总费用为j的方案数。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N];
int w[5] = {0, 10, 20, 50, 100};
int main() {
int n; cin >> n;
f[0] = 1;
for(int i = 1; i <= 4; i++)
for(int j = w[i]; j <= n; j++)
f[j] += f[j-w[i]];
cout << f[n] << endl;
return 0;
}
货币系统1
分析:跟上题类似。也是完全背包问题的裸题。
不过这题要开long long,因为m最大为3000,方案数会很大。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
#define LL long long
const int N = 3010;
LL f[N];
int w[20];
int main() {
int n, m; cin >> n >> m;
f[0] = 1ll;
for(int i = 1; i <= n; i++) cin >> w[i];
for(int i = 1; i <= n; i++)
for(int j = w[i]; j <= m; j++)
f[j] += f[j-w[i]];
cout << f[m] << endl;
return 0;
}
货币系统2
分析:数组b一定有一下性质:
- 数组b中所有元素据来自数组a
- 数组b中的任何一个元素都不能被b中其他元素表示出来
- 数组a中的任何一个元素都可以被表示出来
所以a数组从小到大排序,判断是否有大的数可以被小的数组合,如果有则标记。 结束之后,剩下未标记的必为b数组。
f[j]代表的是:a数组前i个元素中和为j的方案数。 只要方案数不为0,则必有解。
代码:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 110, M = 25010;
int f[M];
int a[N];
int main() {
int t; cin >> t;
while(t--) {
int n; cin >> n;
for(int i = 0; i < n; i++) cin >> a[i];
sort(a, a + n);
int m = a[n-1];
memset(f, 0, sizeof f);
f[0] = 1;
int ans = 0;
for(int i = 0; i < n; i++) {
if(!f[a[i]]) ans++;
for(int j = a[i]; j <= m; j++) {
f[j] += f[j-a[i]];
}
}
cout << ans << endl;
}
return 0;
}
多重背包问题 III
庆功会
分析:这题就是裸的多重背包问题。下面给出朴素版和二进制优化版两种写法。
代码:
朴素版
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 510, M = 6010;
int f[M];
int w[N], v[N], s[N];
int main() {
int n, m; cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> w[i] >> v[i] >> s[i];
for(int i = 1; i <= n; i++) {
for(int j = m; j >= 0; j--) {
for(int k = 0; k <= s[i] && k * w[i] <= j; k++) {
f[j] = max(f[j], f[j-k*w[i]]+k*v[i]);
}
}
}
cout << f[m] << endl;
return 0;
}
二进制优化版
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 50010, M = 6010;
int f[M];
int v[N], w[N];
int main() {
int n, m; cin >> n >> m;
int cnt = 0;
for(int i = 0; i < n; i++) {
int a, b, c; cin >> a >> b >> c;
int k = 1;
while(k < c) {
v[cnt] = a * k;
w[cnt] = b * k;
c -= k;
cnt ++;
k <<= 1;
}
if(c > 0) {
v[cnt] = c * a;
w[cnt] = c * b;
cnt++;
}
}
n = cnt;
for(int i = 0; i < n; i++)
for(int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j-v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
混合背包问题
分析:这题也就是上一题的变形而已。
代码:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 25010, M = 25010;
int f[M];
int w[N], v[N];
int main() {
int n, m;
cin >> n >> m;
int cnt = 0;
for(int i = 0; i < n; i++) {
int a, b, c;
cin >> a >> b >> c;
if(c == -1) c = 1;
else if(c == 0) c = m / a;
int k = 1;
while(k < c) {
w[cnt] = k * a;
v[cnt] = k * b;
c -= k;
k <<= 1;
cnt++;
}
if(c > 0) {
w[cnt] = c * a;
v[cnt] = c * b;
cnt++;
}
}
n = cnt;
for(int i = 0; i < n; i++)
for(int j = m; j >= w[i]; j--)
f[j] = max(f[j], f[j-w[i]] + v[i]);
cout << f[m] << endl;
return 0;
}
二维费用的背包问题
分析:设f[j][k]的含义为:前i前物品,体积不超过j且重量不超过k的最大价值。
则类同于01背包问题,很容易得出状态转移方程。再降维。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N][N];
int W[N], V[N], M[N];
int main() {
int n, v, m; cin >> n >> v >> m;
for(int i = 0; i < n; i++) cin >> V[i] >> M[i] >> W[i];
for(int i = 0; i < n; i++)
for(int j = v; j >= V[i]; j--)
for(int k = m; k >= M[i]; k--)
f[j][k] = max(f[j][k], f[j-V[i]][k-M[i]] + W[i]);
cout << f[v][m] << endl;
return 0;
}
潜水员
分析:
- 状态表示
f[i,j,k]:所有从前i个物品中选,且氧气含量至少是j,氮气含量至少是k的所有选法的气缸重量总和的最小值。 - 状态计算:
- 所有不包含物品i的所有选法:
f[i - 1,j,k] - 所有包含物品i的所有选法:
f[i - 1,j - v1,k - v2]
注意:即使所需要的氧气或者氮气所需的是数量是负数,但其所需数量与0是等价的,因此可以通过所需数量为0来转移
另外附上背包问题中 体积至多是 j ,恰好是 j ,至少是 j 的初始化问题的研究
代码:
- 所有不包含物品i的所有选法:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010, M = 110;
int f[M][M];
int d[N], y[N], w[N];
int main() {
int D, Y, n; cin >> Y >> D >> n;
for(int i = 0; i < n; i++) cin >> y[i] >> d[i] >> w[i];
memset(f, 0x3f, sizeof f);
f[0][0] = 0;
for(int i = 0; i < n; i++)
for(int j = Y; j >= 0; j--)
for(int k = D; k >= 0; k--)
f[j][k] = min(f[j][k], f[max(0, j-y[i])][max(0, k-d[i])] + w[i]);
cout << f[Y][D] << endl;
return 0;
}
机器分配
分析:分组背包问题。难点在于如何求出具体方案数?
在求出最大价值之后,可以通过最后一步推出上一步,进而得到答案。
求具体方案,由于每个公司可以分配不同数量的机器,因此从n遍历到1,假设k为当前公司分配的机器数量,则若满足f[i][j] == f[i - 1][j - k] + w[i][k],其中f[i][j]为当前最优情况,则表示f[i][j]可以从f[i - 1][j - k]状态转移过来,输出当前k值
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20;
int f[N][N];
int w[N][N];
int ans[N];
int main() {
int n, m; cin >> n >> m;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cin >> w[i][j];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++) {
for(int k = 0; k <= j; k++) {
f[i][j] = max(f[i][j], f[i-1][j-k] + w[i][k]);
}
}
cout << f[n][m] << endl;
int t = m;
for(int i = n; i; i--)
for(int j = 0; j <= m; j++) {
if(f[i][t] == f[i-1][t-j] + w[i][j]) {
t -= j;
ans[i] = j;
break;
}
}
for(int i = 1; i <= n; i++) cout << i << ' ' << ans[i] << endl;
return 0;
}
开心的金明
分析:01背包问题的裸题。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 30, M = 30010;
int f[M];
int v[N], w[N];
int main() {
int n, m; cin >> m >> n;
for(int i = 0; i < n; i++) {
int p; cin >> v[i] >> p;
w[i] = v[i] * p;
}
for(int i = 0; i < n; i++) {
for(int j = m; j >= v[i]; j--) {
f[j] = max(f[j], f[j-v[i]] + w[i]);
}
}
cout << f[m] << endl;
return 0;
}
有依赖的背包问题
分析:这题是没有上升的舞会+分组背包问题的结合。每一颗子树都可以看成一组背包。
f[u][j]的含义:以节点u为根节点的子树,体积不超过j的最大价值。由于根节点必选,因此可以先不考虑根节点。
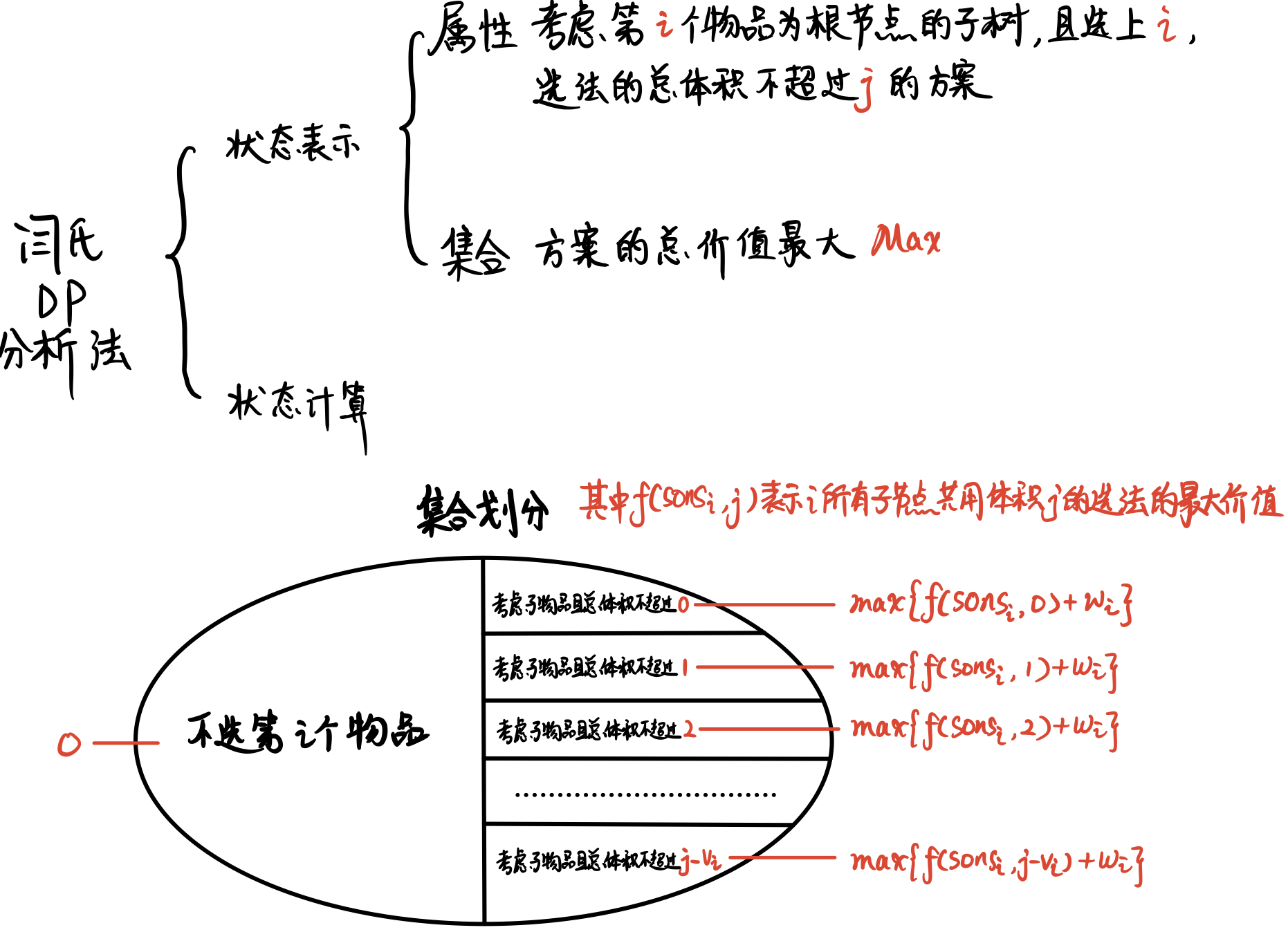
代码:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 110;
int f[N][N];
int h[N], e[N], ne[N], idx;
int v[N], w[N]; // 体积、价值
bool st[N];
int n, m;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u) {
for(int i = h[u]; ~i; i = ne[i]) {
dfs(e[i]);
for(int j = m - v[u]; j >= 0; j--) {
for(int k = 0; k <= j; k++) {
f[u][j] = max(f[u][j], f[u][j-k] + f[e[i]][k]);
}
}
}
for(int i = m; i >= v[u]; i--) f[u][i] = f[u][i-v[u]] + w[u];
for(int i = 0; i < v[u]; i++) f[u][i] = 0;
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
int root = 1;
for(int i = 1; i <= n; i++) {
int f; cin >> v[i] >> w[i] >> f;
if(f == -1) root = i;
else add(f, i);
}
dfs(root);
cout << f[root][m] << endl;
return 0;
}
背包问题求方案数
分析:这题很类似与最短路问题。当遇到更优的方案时,将方案数更新,遇到选法相同的方案时,加上该方案数。
因此需要再开一个数组存方案数。
f[i]用来存储背包容积为 i时的最佳方案的总价值,
cnt[i]为背包容积为 i 时总价值为最佳的方案数
先初始化所有的cnt[i]为1,因为背包里什么也不装也是一种方案
外层循环n次,每次读入新物品的 v,w。
求出装新物品时的总价值,与不装新物品时作对比
如果装新物品的方案总价值更大,那么用f[j−v]+w 来更新f[j],用 cnt[j−v] 更新 cnt[j]
如果总价值相等,那么最大价值的方案数就多了 cnt[j−v] 种
代码:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int f[N];
int cnt[N];
int w[N], v[N];
int main() {
int n, m; cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 0; i <= m; i++) cnt[i] = 1;
for(int i = 1; i <= n; i++) {
for(int j = m; j >= v[i]; j--) {
if(f[j-v[i]] + w[i] > f[j]) {
f[j] = f[j-v[i]] + w[i];
cnt[j] = cnt[j-v[i]];
}else if(f[j-v[i]] + w[i] == f[j]) {
cnt[j] = (cnt[j] + cnt[j-v[i]]) % mod;
}
}
}
cout << cnt[m] << endl;
return 0;
}
背包问题求具体方案
分析:通过本题可以得出一个结论:01背包问题不一定非要从前往后选,也可以从后往前选。
由于要输出字典序最小的最优方案,所以本题从后往前选,然后在输出具体方案的时候,从前往后,这样就可以答案从结论推到过程的目的了。
可以得出本题和机器分配相似。
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N][N];
int w[N], v[N];
int main() {
int n, m; cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = n; i >= 1; i--)
for(int j = 0; j <= m; j++) {
f[i][j] = f[i+1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i+1][j-v[i]] + w[i]);
}
int t = m;
for(int i = 1; i <= n; i++) {
if(f[i][t] == f[i+1][t-v[i]] + w[i] && t >= v[i]) {
cout << i << ' ';
t -= v[i];
}
}
return 0;
}
能量石
分析: 假设先选第i个物品再选第i+1个物品,则能量获得与损失的情况应该是: 。
若先选第i+1个物品再选第i个物品,能力获得与损失的情况为:。
基于贪心的思想,我们可以得出,要使得整体获得最大能量,应该有:
即:
通过这个式子,可以得出应该把单位时间流失多的放到前面。最后再套一个01背包。
其中:f[i][j] 表示:前i个物品中,时间为j所获得的最大能量。
则f[i][j]的状态转移方程为: 如果时间太长,能力最低流失到0,不可能为负数。
代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110, M = 10010;
int f[M];
struct node {
int s, e, l;
}w[M];
bool cmp(node a, node b) {
return a.s * b.l < b.s * a.l;
}
int main() {
int T; cin >> T;
for(int c = 1; c <= T; c++) {
memset(f, 0, sizeof f);
int n; cin >> n;
int m = 0;
for(int i = 0; i < n; i++) cin >> w[i].s >> w[i].e >> w[i].l, m += w[i].s;
sort(w, w + n, cmp);
for(int i = 0; i < n; i++)
for(int j = m; j >= w[i].s; j--) {
int x = w[i].e - w[i].s * w[i+1].l;
f[j] = max(f[j], f[j-w[i].s] + max(0, w[i].e - w[i].l * (j - w[i].s)));
}
int ans = 0;
for(int i = 0; i <= m; i++) ans = max(ans, f[i]);
printf("Case #%d: %d\n", c, ans);
}
return 0;
}
金明的预算方案
分析:本题类似于有依赖关系的背包问题+开心的金明结合。只不过每种附属品有选和不选两张状态。因此可以通过状态压缩的方法,枚举每一种情况。
每一个主件和其附属品都可以看成是一组背包。
代码:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
#define v first
#define w second
#define pb push_back
typedef pair<int,int>PII;
const int N = 60, M = 32010;
PII master[N];
vector<PII>servant[N];
int f[M];
int n, m;
int main() {
cin >> m >> n;
for(int i = 1; i <= n; i++) {
int a, b, c;
cin >> a >> b >> c;
b *= a;
if(c == 0) master[i] = {a,b};
else servant[c].pb({a,b});
}
for(int i = 1; i <= n; i++)
for(int u = m; u >= 0; u--)
for(int j = 0; j < 1 << servant[i].size(); j++) {
int v = master[i].v, w = master[i].w;
for(int k = 0; k < servant[i].size(); k++) {
if(j >> k & 1) {
v += servant[i][k].v;
w += servant[i][k].w;
}
}
if(u >= v) f[u] = max(f[u], f[u-v] + w);
}
cout << f[m] << endl;
return 0;
}
状态机模型
大盗阿福
分析:f[i][1]表示抢第i个店铺的最大收益,f[i][0]表示不抢第i个店铺的最大收益
由于不能抢相邻的,所以抢第i个店铺时一定不能抢第i−1个店铺
抢第i个店铺时的最大收益为f[i−1][0]+w[i],不抢第i个店铺时的最大收益为:max(f[i-1][1],f[i-1][0]) 很类似于没有上司的舞会`
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int w[N];
int f[N][2];
int main() {
int T; cin >> T;
while(T--) {
int n; cin >> n;
for(int i = 1; i <= n; i++) cin >> w[i];
for(int i = 1; i <= n; i++) {
f[i][0] = max(f[i-1][1], f[i-1][0]);
f[i][1] = f[i-1][0] + w[i];
}
cout << max(f[n][0], f[n][1]) << endl;
}
return 0;
}
股票买卖 IV
分析: 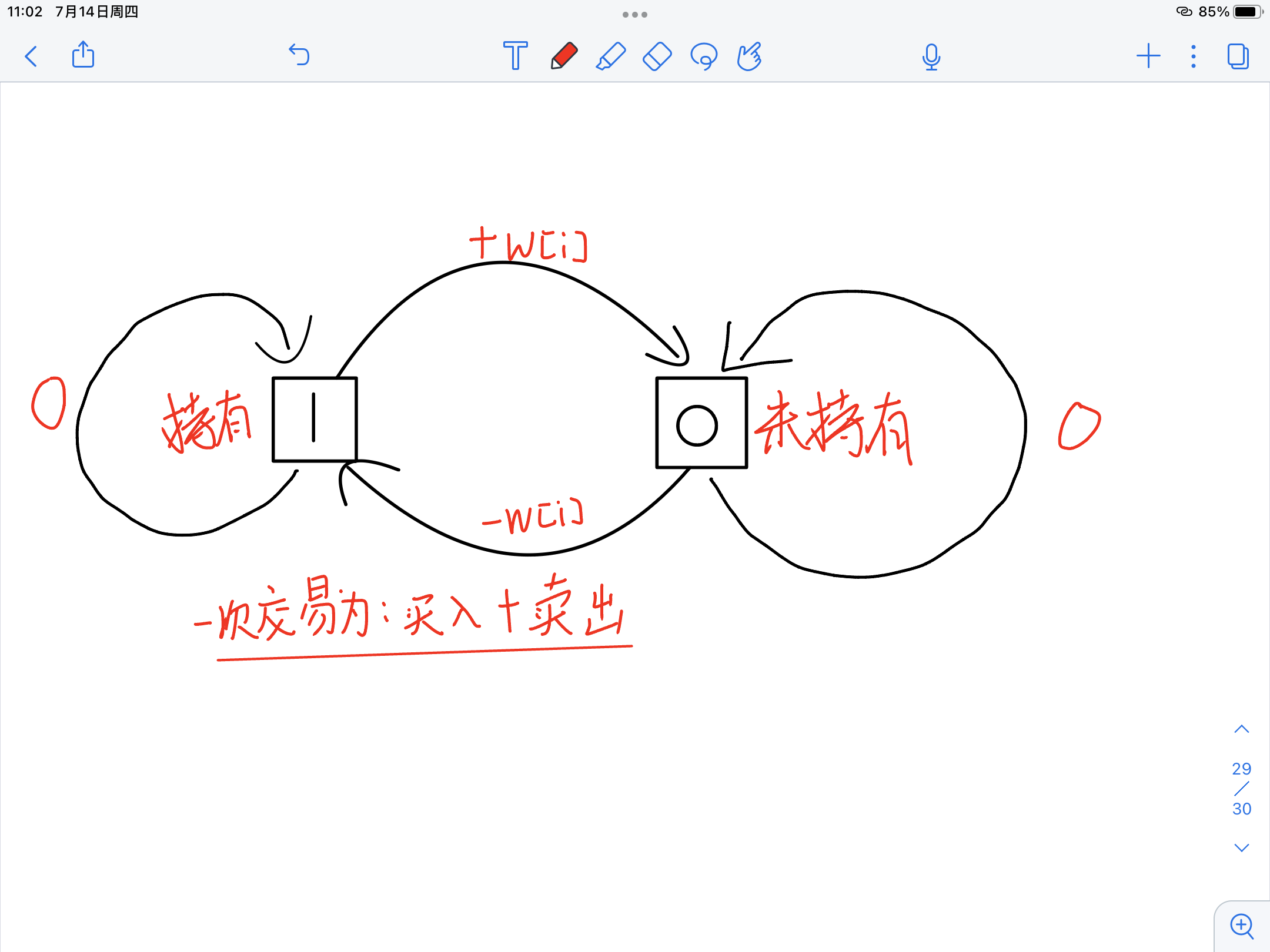
f[i][j][0]表示第i天交易了j次且手中无股票的最大收益,f[i][j][1]表示第i天交易了j次且手中有股票的最大收益。
代码:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 100010;
int w[N];
int f[N][110][2];
int main() {
int n, m; cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> w[i];
memset(f, 0xcf, sizeof f);
for(int i = 0; i <= n; i++) f[i][0][0] = 0;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
f[i][j][0] = max(f[i-1][j][1] + w[i], f[i-1][j][0]);
f[i][j][1] = max(f[i-1][j-1][0] - w[i], f[i-1][j][1]);
}
}
int ans = 0;
for(int i = 0; i <= m; i++) ans = max(ans, f[n][i][0]);
cout << ans << endl;
return 0;
}
用滚动数组优化空间:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 100010;
int w[N];
int f[2][110][2];
int main() {
int n, m; cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> w[i];
memset(f, 0xcf, sizeof f);
for(int i = 0; i < 2; i++) f[i][0][0] = 0;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
f[i&1][j][0] = max(f[(i-1)&1][j][1] + w[i], f[(i-1)&1][j][0]);
f[i&1][j][1] = max(f[(i-1)&1][j-1][0] - w[i], f[(i-1) & 1][j][1]);
}
}
int ans = 0;
for(int i = 0; i <= m; i++) ans = max(ans, f[n & 1][i][0]);
cout << ans << endl;
return 0;
}
股票买卖 V
分析: 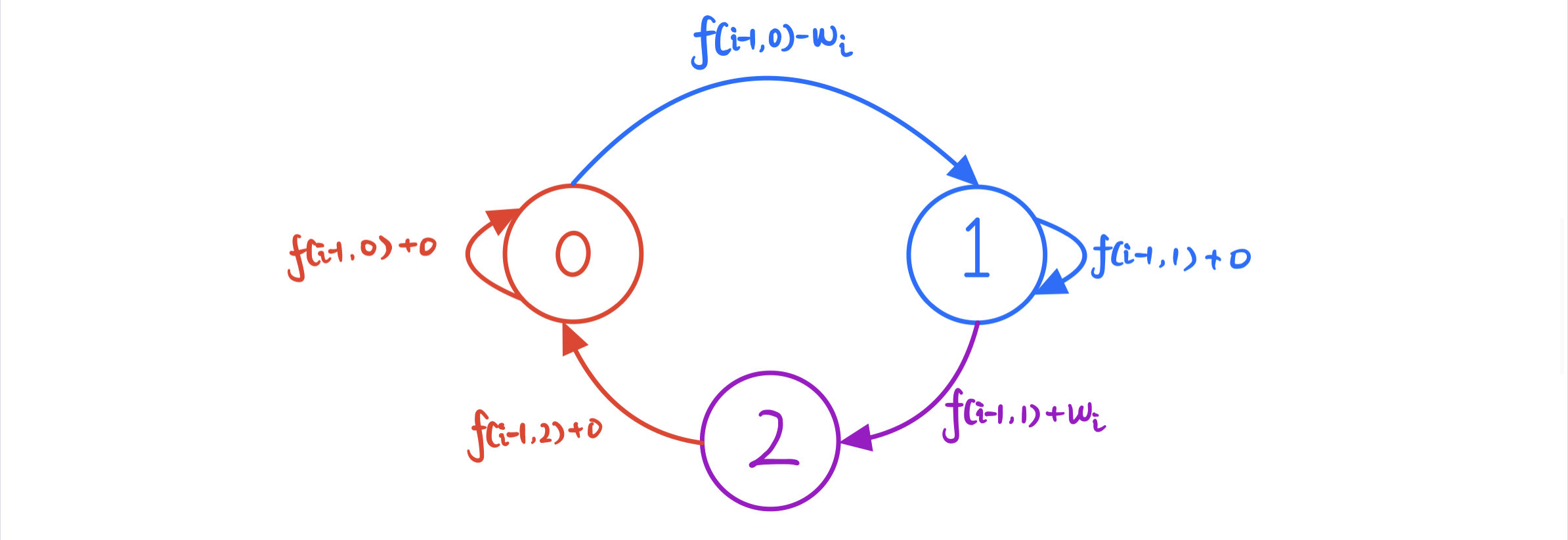
如果第 i 天是 空仓 (j=0) 状态,则 i-1 天可能是 空仓 (j=0) 或 冷冻期 (j=2) 的状态
如果第 i 天是 冷冻期 (j=2) 状态,则 i-1 天只可能是 持仓 (j=1) 状态,在第 i 天选择了 卖出
如果第 i 天是 持仓 (j=1) 状态,则 i-1 天可能是 持仓 (j=1) 状态 或 空仓 (j=0) 的状态 (买入)
代码:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;
int w[N];
int f[N][3];
int main() {
int n; cin >> n;
for(int i = 1; i <= n; i++) cin >> w[i];
memset(f, 0xcf, sizeof f);
f[0][0] = 0;
for(int i = 1; i <= n; i++) {
f[i][0] = max(f[i-1][0], f[i-1][2]);
f[i][1] = max(f[i-1][1], f[i-1][0] - w[i]);
f[i][2] = f[i-1][1] + w[i];
}
cout << max(f[n][2], f[n][0]) << endl;
return 0;
}
设计密码
修复DNA
第二章搜索
Flood Fill
池塘计数
第三章 图论
单源最短路的建图方式
热浪
代码:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int,int>PII;
const int N = 2510, M = 6210 << 1;
int h[M], e[M], ne[M], w[M], idx;
bool st[N];
int dist[N];
int n, m, sta, en;
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void dijstra() {
memset(dist, 0x3f, sizeof dist);
dist[sta] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, sta});
while(heap.size()) {
auto top = heap.top();
heap.pop();
int a = top.first, b = top.second;
if(st[b]) continue;
st[b] = true;
for(int i = h[b]; i != -1; i = ne[i]) {
int j = e[i];
if(dist[j] > a + w[i]) {
dist[j] = a + w[i];
heap.push({dist[j], j});
}
}
}
}
int main() {
cin >> n >> m >> sta >> en;
memset(h, -1, sizeof h);
while(m--) {
int a, b, c; cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
dijstra();
cout << dist[en] << endl;
return 0;
}
信使
分析:找到距离起点最远的点的距离。因为时间是同步的。
代码:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int,int>PII;
const int N = 110, M = 210 << 1;
int h[M], e[M], ne[M], w[M], idx;
bool st[N];
int dist[N];
int n, m;
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void dijstra() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1});
while(heap.size()) {
auto top = heap.top();
heap.pop();
int a = top.first, b = top.second;
if(st[b]) continue;
st[b] = true;
for(int i = h[b]; i != -1; i = ne[i]) {
int j = e[i];
if(dist[j] > a + w[i]) {
dist[j] = a + w[i];
heap.push({dist[j], j});
}
}
}
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
while(m--) {
int a, b, c; cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
dijstra();
int ans = 0;
for(int i = 1; i <= n; i++) {
ans = max(ans, dist[i]);
}
if(ans == 0x3f3f3f3f) cout << -1 << endl;
else cout << ans << endl;
return 0;
}
香甜的黄油
分析:暴力枚举每一个点,取最小值。
代码:
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
typedef pair<int,int>PII;
const int N = 810, M = 1500 << 1;
int h[M], e[M], ne[M], w[M], idx;
int cows[N];
int k, n, m;
bool st[N];
int dist[N];
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int dijstra(int u) {
memset(dist, 0x3f, sizeof dist);
memset(st, false, sizeof st);
dist[u] = 0;
priority_queue<PII, vector<PII>, greater<PII>>heap;
heap.push({0, u});
while(heap.size()) {
auto top = heap.top();
heap.pop();
int x = top.second;
if(st[x]) continue;
st[x] = true;
for(int i = h[x]; i != -1; i = ne[i]) {
int j = e[i];
if(dist[j] > dist[x] + w[i]) {
dist[j] = dist[x] + w[i];
heap.push({dist[j], j});
}
}
}
int ans = 0;
for(int i = 1; i <= k; i++) {
if(dist[cows[i]] == 0x3f3f3f3f) return 0x3f3f3f3f;
ans += dist[cows[i]];
}
return ans;
}
int main() {
cin >> k >> n >> m;
memset(h, -1, sizeof h);
for(int i = 1; i <= k; i++) {
int id; cin >> id;
cows[i] = id;
}
while(m--) {
int a, b, c; cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
int ans = 0x3f3f3f3f;
for(int i = 1; i <= n; i++)
ans = min(ans, dijstra(i));
cout << ans << endl;
return 0;
}
最小花费
分析:这题的边权应该取最大值,因为只有扣除的钱越小,起始的钱才能越小,因此剩下的钱应该越大越好。
代码:
#include <algorithm>
#include <cstring>
#include <queue>
#include <iostream>
using namespace std;
typedef pair<double, int> PII;
const int N = 2010, M = 2e5 + 10;
int h[M], e[M], ne[M], idx;
double dist[N], w[M];
int n, m, A, B;
bool st[N];
void add(int a, int b, double c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void dijstra() {
dist[A] = 1.0;
priority_queue<PII, vector<PII>, less<PII>> heap;
heap.push({1.0, A});
while(heap.size()) {
auto t = heap.top();
heap.pop();
int b = t.second;
if(st[b]) continue;
for(int i = h[b]; i != -1; i = ne[i]) {
int j = e[i];
if(dist[j] < dist[b] * w[i]) {
dist[j] = dist[b] * w[i];
heap.push({dist[j], j});
}
}
}
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
while(m--) {
int a, b;
double c;
cin >> a >> b >> c;
c = (100.0-c)/100.0;
add(a, b, c), add(b, a, c);
}
cin >> A >> B;
dijstra();
printf("%.8f\n", 100.0/dist[B]);
return 0;
}
最优乘车
分析:把每列班车经过的点都连起来,边权为1。建图。
代码:
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#include <sstream>
using namespace std;
typedef pair<int,int>PII;
const int N = 510, M = 1e5 + 10;
int h[M], e[M], ne[M], idx;
int dist[N];
bool st[N];
int stop[N];
int n, m;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dijstra() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>>heap;
heap.push({0,1});
while(heap.size()) {
auto t = heap.top();
heap.pop();
int x = t.second;
if(st[x]) continue;
st[x] = true;
for(int i = h[x]; i != -1; i = ne[i]) {
int j = e[i];
if(dist[j] > dist[x] + 1) {
dist[j] = dist[x] + 1;
heap.push({dist[j], j});
}
}
}
}
int main() {
cin >> m >> n;
memset(h, -1, sizeof h);
getchar();
while(m--) {
string line;
getline(cin, line);
int cnt = 0, p;
stringstream ssin(line);
while(ssin >> p) stop[cnt++] = p;
for(int i = 0; i < cnt; i++)
for(int j = i + 1; j < cnt; j++)
add(stop[i], stop[j]);
}
dijstra();
if(dist[n] == 0x3f3f3f3f) cout << "NO" << endl;
else cout << dist[n] - 1 << endl;
return 0;
}
昂贵的聘礼
分析:
- 建立一个超级源点0,从0建立一条边到每个物品,权值为物品的价值。代表花费多少钱就可以购买这个物品。
- 若某个物品拥有替代品,代表从替代品建立一条边到这个物品,价值为替代的价值。 代表我有了这个替代品,那么还需要花费多少就能买这个物品。
- 最后就是等级制度。我们可以枚举每个等级区间,每次求最短路是只能更新在这个区间里面的物品。枚举所有情况求一个最小值就可以了。 特别注意的是区间必须包含1点。 那么范围就是【L[1] - m, L[1]】
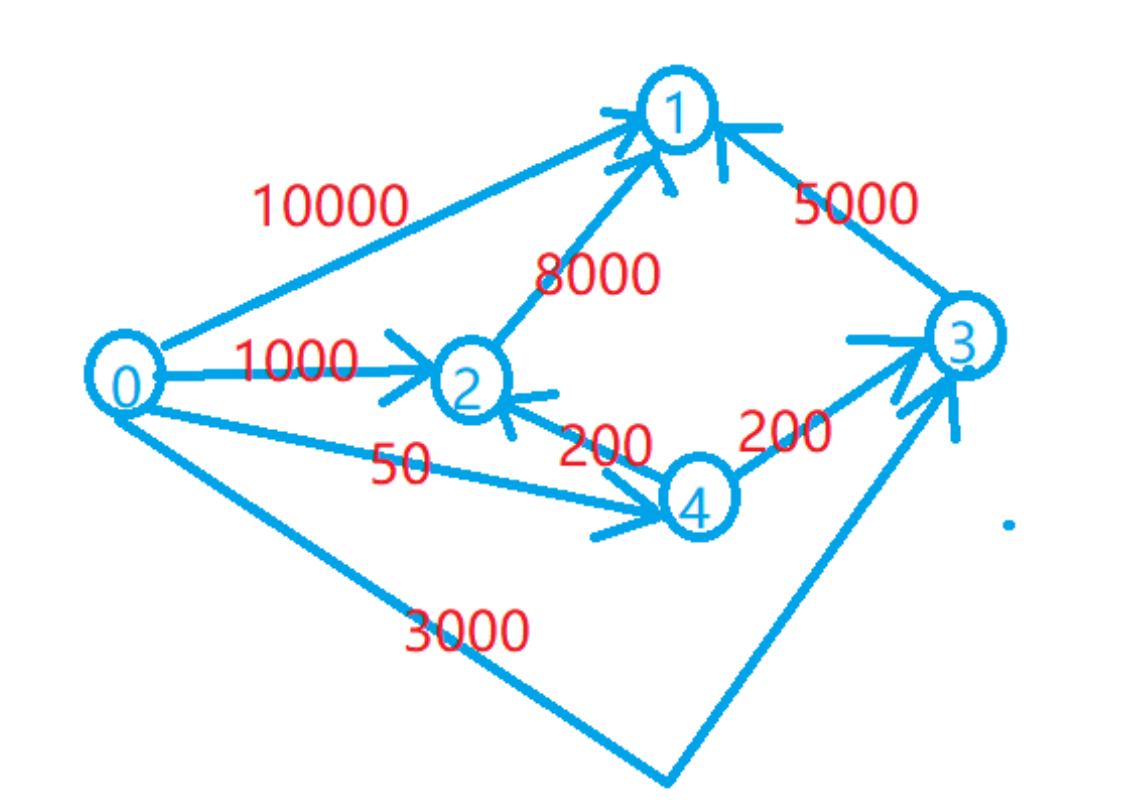
代码:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 110;
int g[N][N], level[N];
int dist[N];
bool st[N];
int n, m;
int dijstra(int down, int up) {
memset(dist, 0x3f, sizeof dist);
memset(st, false, sizeof st);
dist[0] = 0;
for(int i = 0; i <= n; i++) {
int t = -1;
for(int j = 0; j <= n; j++)
if(!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
st[t] = true;
for(int j = 1; j <= n; j++)
if(level[j] >= down && level[j] <= up)
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
return dist[1];
}
int main() {
cin >> m >> n;
memset(g, 0x3f, sizeof g);
for(int i = 1; i <= n; i++) g[i][i] = 0;
for(int i = 1; i <= n; i++) {
int p, cnt; cin >> p >> level[i] >> cnt;
g[0][i] = min(g[0][i], p);
while(cnt--) {
int id, cost;
cin >> id >> cost;
g[id][i] = min(g[id][i], cost);
}
}
int ans = 0x3f3f3f3f;
for(int i = level[1] - m; i <= level[1]; i++) ans = min(ans, dijstra(i, i + m));
cout << ans << endl;
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 如何调用 DeepSeek 的自然语言处理 API 接口并集成到在线客服系统
· 【译】Visual Studio 中新的强大生产力特性
· 2025年我用 Compose 写了一个 Todo App