爬山算法与模拟退火
爬山算法
简介
爬山算法是一种局部择优的方法,该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。更加形象些来讲,就是在迷雾中爬上山峰。
局部搜索算法
所谓局部搜索算法,就是只对局部的状态空间进行搜索,从而得出局部最优解的算法。这种算法的优点在于不用考虑时空间,我们始终是在自己规定的状态空间内进行遍历,得出新的状态后就替换掉旧的状态,保证局部状态空间大小不变。
怎么爬
规定一个起始点,从起始状态开始查询附近的状态,哪里高往哪里爬。即对于每个当前最优方案 x,在与之相邻的状态中选择一个新方案 x',如果这个新的解 x' 更优,则转移过去,否则不变。
不可忽视的致命短处——迷雾
之前提到,爬山是在迷雾中攀爬。也就是说,尽管你爬到了某个小山的山顶,但是因为大雾漫天,挡住了你的视线,所以你并不知道远处是否还有更高的山峰,只知道你目前所处位置相较于前后一个短区间内是最高的(例如下图)。这是爬山算法的致命性短处,如果题目非单峰函数,爬山算法在大几率上会陷入局部最优解。
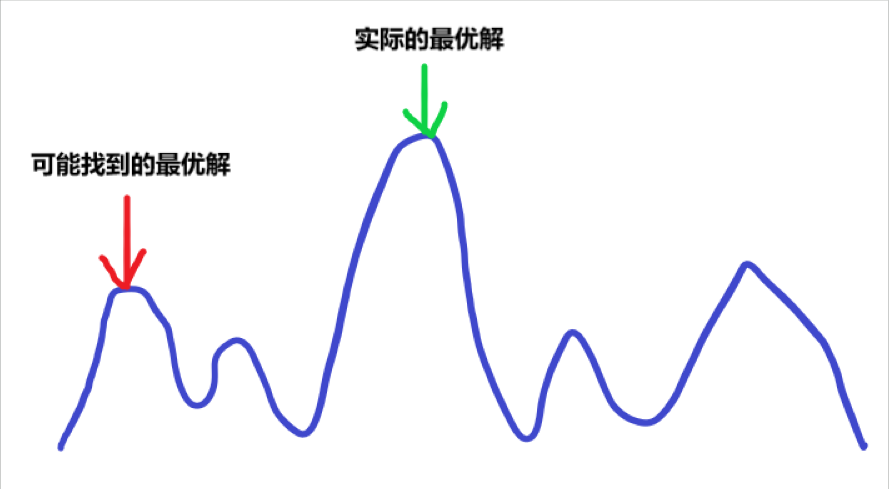
优化
为了尽可能获取优秀的答案,我们可以多次爬山。方法有修改初始状态/修改降温参数/修改初始温度等,然后开一个全局最优解记录答案。每次爬山结束之后,更新全局最优解。然而这样处理可能会存在的问题是超时。
具体实现
爬山算法一般会引入温度参数(类似模拟退火)。类比地说,爬山算法就像是一只兔子喝醉了在山上跳,它每次都会朝着它所认为的更高的地方(这往往只是个不准确的趋势)跳,显然它有可能一次跳到山顶,也可能跳过头翻到对面去。不过没关系,兔子翻过去之后还会跳回来。显然这个过程很没有用,兔子永远都找不到出路,所以在这个过程中兔子冷静下来并在每次跳的时候更加谨慎,少跳一点,以到达合适的最优点。
兔子逐渐变得清醒的过程就是降温过程,即温度参数在爬山的时候会不断减小。
关于降温:降温参数是略小于 1 的常数,一般在 [0.985, 0.999] 中选取。
例1:[JSOI2008]球形空间产生器
-
初始化球心为各个给定点的重心(即其各维坐标均为所有给定点对应维度坐标的平均值)
-
对于当前的球心,求出每个已知点到这个球心欧氏距离的平均值
-
遍历所有点,记录一个改变值 cans(分开每一维度记录),对于每一个点的欧氏距离,如果大于平均值,就把改变值加上差值,否则减去。实际上并不用判断这个大小问题,只要不考虑绝对值,直接用坐标计算即可。这个过程可以形象地转化成一个新的球心,在空间里推来推去,碰到太远的点就往点的方向拉一点,碰到太近的点就往点的反方向推一点
-
将我们记录的 cans 乘上温度,更新球心,回到步骤 2
-
在温度小于某个给定阈值的时候结束
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4 + 10;
int n;
double tot;
double ans[maxn], cans[maxn], dis[maxn], f[maxn][maxn];
inline double check() {
tot = 0;
for (int i = 1; i <= n + 1; i++) {
dis[i] = 0;
cans[i] = 0;
for (int j = 1; j <= n; j++)
dis[i] += (f[i][j] - ans[j]) * (f[i][j] - ans[j]);
dis[i] = sqrt(dis[i]);
tot += dis[i];
}
tot /= (n + 1);
for (int i = 1; i <= n + 1; i++)
for (int j = 1; j <= n; j++) //对于每个维度把修改值更新掉,欧氏距离差*差值贡献
cans[j] += (dis[i] - tot) * (f[i][j] - ans[j]) / tot;
}
int main() {
cin >> n;
for (int i = 1; i <= n + 1; i++)
for (int j = 1; j <= n; j++) {
cin >> f[i][j];
ans[j] += f[i][j];
}
for (int i = 1; i <= n; i++) ans[i] = ans[i] / (n + 1);
//不断降温,参数需要手动调,实测 0.9999 会 wa 一个点,0.99999 超时 3 个点
for (double t = 10001; t >= 0.0001; t *= 0.99995) {
check();
for (int i = 1; i <= n; i++) ans[i] += cans[i] * t;
}
for (int i = 1; i <= n; i++) printf("%.3f ", ans[i]);
return 0;
}
例2:[JSOI2004]平衡点 / 吊打XXX
同上题大差不离
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4 + 10;
int n;
int x[maxn], y[maxn], w[maxn];
double ansx, ansy, totx, toty;
inline double check() {
totx = 0; toty = 0;
for (int i = 1; i <= n; i++) {
double numx = (x[i] - ansx) * (x[i] - ansx);
double numy = (y[i] - ansy) * (y[i] - ansy);
double dis = sqrt(numx + numy);
if (dis == 0.0) continue;
totx += w[i] * (x[i] - ansx) / dis;
toty += w[i] * (y[i] - ansy) / dis;
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> x[i] >> y[i] >> w[i];
ansx += x[i]; ansy += y[i];
}
ansx /= n; ansy /= n;
for (double t = 10001; t >= 0.0001; t *= 0.999) {
check();
ansx += totx * t; ansy += toty * t;
}
printf("%.3f %.3f\n", ansx, ansy);
return 0;
}
模拟退火
简介
模拟退火是一种随机化算法。当一个问题的方案数量极大(甚至是无穷的)而且不是一个单峰函数时,我们常使用模拟退火求解。
实现
根据爬山算法的过程,我们发现:对于一个当前最优解附近的非最优解,爬山算法直接舍去了这个解。而很多情况下,我们需要去接受这个非最优解从而跳出这个局部最优解,即为模拟退火算法。模拟退火其实也是一种贪心算法,但是它的搜索过程引入了随机因素,它以一定的概率来接受一个比当前解要差的解,因此有可能会跳出这个局部的最优解,达到全局的最优解。
模拟退火算法描述
先用一句话概括:如果新状态的解更优则修改答案,否则以一定概率接受新状态。
我们定义当前温度为 T,新状态与已知状态(由已知状态通过随机的方式得到)之间的能量(值)差为 ∆E(∆E ≥ 0),则发生状态转移(修改最优解)的概率为
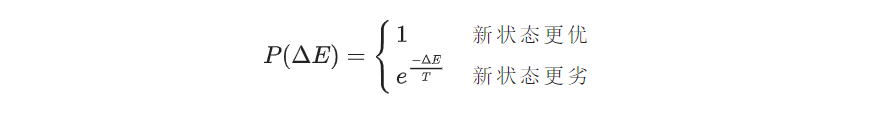
注意:我们有时为了使得到的解更有质量,会在模拟退火结束后,以当前温度在得到的解附近多次随机状态,尝试得到更优的解(其过程与模拟退火相似)。
如何退火
模拟退火时我们有三个参数:初始温度 T0,降温系数 d,终止温度 Tk。其中 T0 是一个比较大的数,d 是一个非常接近 1 但是小于 1 的数,Tk 是一个接近 0 的正数。
首先让温度 T = T0,然后按照上述步骤进行一次转移尝试,再让 T = d * T。当 T < Tk 时模拟退火过程结束,当前最优解即为最终的最优解。
注意为了使得解更为精确,我们通常不直接取当前解作为答案,而是在退火过程中维护遇到的所有解的最优值。
引用一张 Wiki - Simulated annealing 的图片(随着温度的降低,跳跃越来越不随机,最优解也越来越稳定)。
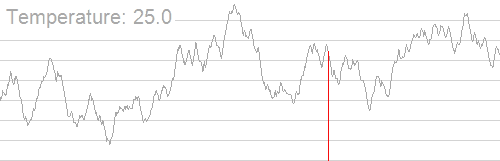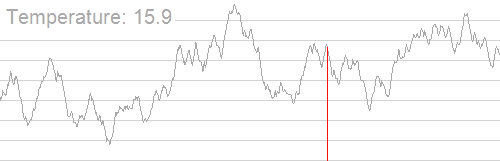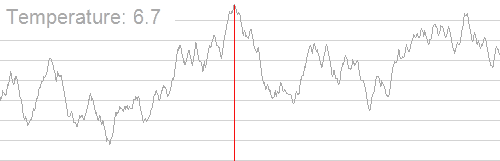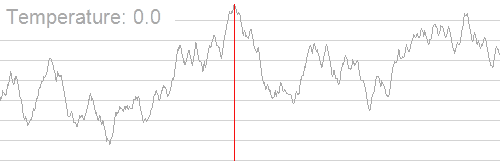
例题
例1:[JSOI2004]平衡点 / 吊打XXX
参数真的太难调了,OI wiki 给出的代码只有 66 分,自己调了一会 wa 了十几次,借用了题解区第一篇题解的参数才 A 了,难绷
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e4 + 10;
int n;
int x[maxn], y[maxn], w[maxn];
double ansx, ansy, dis;
inline double calc(double xx, double yy) {
double res = 0;
for (int i = 1; i <= n; i++) {
double dx = x[i] - xx, dy = y[i] - yy;
res += sqrt(dx * dx + dy * dy) * w[i];
}
return res;
}
inline void simulateAnneal() {
double t = 3000;
while (t > 1e-15) {
double nxtx = ansx + t * (rand() * 2 - RAND_MAX); //随机产生新的答案
double nxty = ansy + t * (rand() * 2 - RAND_MAX);
double nxtw = calc(nxtx, nxty);
double delta = nxtw - dis;
if (delta < 0) { //如果此答案更优,就接受
ansx = nxtx; ansy = nxty; dis = nxtw;
}
else if (exp(-delta / t) * RAND_MAX > rand()) ansx = nxtx, ansy = nxty; //否则根据多项式概率接受
t *= 0.996;
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> x[i] >> y[i] >> w[i];
ansx += x[i]; ansy += y[i];
}
ansx /= n; ansy /= n;
dis = calc(ansx, ansy);
simulateAnneal(); //多跑几遍退火,增加得到最优解的概率
simulateAnneal();
simulateAnneal();
simulateAnneal();
printf("%.3f %.3f\n", ansx, ansy);
return 0;
}
内容参考:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号