树链剖分
参考博客:树链剖分详解
树链剖分的引入
先回顾两个问题:
1、将树从x到y结点最短路径上所有节点的值都加上z
我们很容易想到,树上差分可以以 O(n+m) 的优秀复杂度解决这个问题
2、求树从x到y结点最短路径上所有节点的值之和
lca大水题,我们又很容易地想到,dfs O(n)预处理每个节点的 dis(即到根节点的最短路径长度)
然后对于每个询问,求出 x,y 两点的 lca,利用lca的性质 distance(x,y) = dis (x) + dis (y) - 2 * dis (lca)求出结果
时间复杂度 O(mlogn+n)
现在来思考一个问题:
如果刚才的两个问题结合起来,成为一道题的两种操作呢?刚才的方法显然就不够优秀了(每次询问之前要跑dfs更新dis)
此时树链剖分华丽登场,树剖是通过轻重边将树分割成多条链,然后利用数据结构来维护这些链(本质上是一种优化暴力)
树链剖分详解
首先明确以下几个概念:
-
重儿子:父亲节点的所有儿子中子树结点数目最多(size最大)的结点
-
轻儿子:父亲节点中除了重儿子以外的儿子
-
重边:父亲结点和重儿子连成的边
-
轻边:父亲节点和轻儿子连成的边
-
重链:由多条重边连接而成的路径
-
轻链:由多条轻边连接而成的路径

比如上图中,用黑线连接的结点都是重结点,其余均是轻结点
2-11 就是重链,2-5 就是轻链,用红点标记的就是该结点所在的重链的起点,也就是下文提到的 top 结点
还有每条边的值其实是进行 dfs 时的执行序号
然后通过观察可以发现:并不是轻儿子之后全是轻儿子,非叶节点有且只有1个重儿子。所以当一个节点选了他的重儿子之后,我们并不能保证它的轻儿子就是叶节点,所以我们就以这个轻儿子为根,再去选这个轻儿子的轻重儿子,也就是一个 dfs 的过程,这样我们就会得到很多重链
变量声明
struct node{
int to, nxt;
}e[maxn * 2];
struct Node{
int sum, num;
}ed[maxn * 4];
int head[maxn], cnt, tot, son[maxn], a[maxn], fa[maxn];
int size[maxn], dep[maxn], top[maxn], id[maxn], ran[maxn];
其中:
- fa[u]:保存结点 u 的父亲节点
- dep[u]:保存结点 u 的深度值
- size[u]:保存以 u 为根的子树节点个数
- son[u]:保存重儿子
- ran[u]:保存当前 dfs 标号在树中所对应的节点
- top[u]:保存当前节点所在链的顶端节点
- id[u]:保存树中每个节点剖分以后的新编号(dfs 的执行顺序)
树链剖分的实现
Step1
对于一个点我们首先求出它所在的子树大小,找到它的重儿子(即处理出 size,son 数组)
Step2
在 dfs 过程中顺便记录其父亲以及深度(即处理出 f,d 数组)
操作 1,2 可以通过一遍 dfs 完成
inline void dfs1(int x, int fat) {
size[x] = 1; //这个点本身 size=1
for (int i = head[x]; i; i = e[i].nxt) {
int v = e[i].to;
if (v == fat) continue;
fa[v] = x;
dep[v] = dep[x] + 1; //层次深度+1
dfs1(v, x);
size[x] += size[v]; //子节点的 size 已被处理,用它来更新父节点的 size
if (size[v] > size[son[x]]) son[x] = v; //选取size最大的作为重儿子
}
}
//进入
dfs1(root,0);
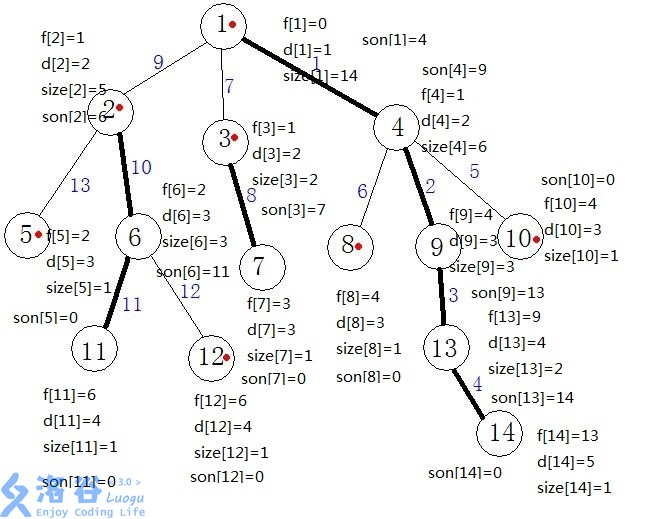
dfs 跑完如图所示
Step3
跑第二遍 dfs,然后连接重链,同时标记每一个节点的 dfs 序,并且为了用数据结构来维护重链,我们在 dfs 时保证一条重链上各个节点 dfs 序连续(即处理出数组 top,id,rk)
inline void dfs2(int u, int t) { //当前节点、重链顶端
top[u] = t;
id[u] = ++tot; //标记 dfs 序
ran[tot] = u; //序号 cnt 对应节点 u
if (!son[u]) return;
dfs2(son[u], t);
/*我们选择优先进入重儿子来保证一条重链上各个节点dfs序连续,
一个点和它的重儿子处于同一条重链,所以重儿子所在重链的顶端还是t*/
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (v != son[u] && v != fa[u]) dfs2(v, v); //一个点位于轻链底端,那么它的top必然是它本身
}
return;
}
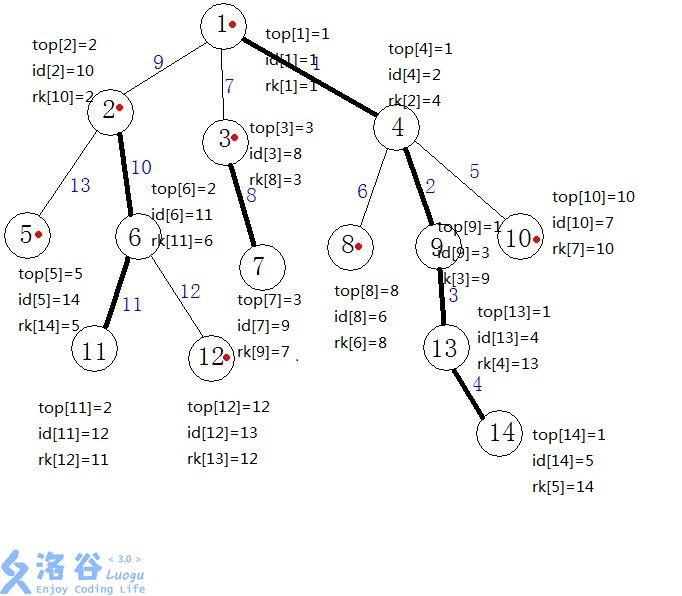
跑完是这样
Step4
两遍 dfs 就是树链剖分的主要处理,通过 dfs 我们已经保证一条重链上各个节点dfs序连续,那么可以想到通过数据结构(以线段树为例)来维护一条重链的信息
回顾上文的那个题目,修改和查询操作原理是类似的,以查询操作为例,其实就是个 LCA,不过这里使用了 top 来进行加速,因为 top 可以直接跳转到该重链的起始结点(轻链没有起始结点之说,他们的top 就是自己)。需要注意的是,每次循环只能跳一次,并且让结点深的那个来跳到 top 的位置,避免两个一起跳从而擦肩而过
inline int sum(int x, int y) {
int ans = 0;
int fax = top[x], fay = top[y];
while (fax != fay) { //两点不在同一条重链
if (dep[fax] < dep[fay]) {
swap(x, y); swap(fax, fay);
}
ans += query(1, 1, tot, id[fax], id[x]); //线段树区间求和,处理这条重链的贡献
x = fa[fax]; fax = top[x]; //将x设置成原链头的父亲结点,走轻边,继续循环
}
//循环结束,两点位于同一重链上,但两点不一定为同一点,所以我们还要统计这两点之间的贡献
if (id[x] > id[y]) swap(x, y);
ans += query(1, 1, tot, id[x], id[y]);
return ans;
}
模板及例题
题目描述
一棵树上有 n 个节点,编号分别为 1 到 n,每个节点都有一个权值 w。
我们将以下面的形式来要求你对这棵树完成一些操作:
I. CHANGE u t : 把结点 u 的权值改为 t。
II. QMAX u v: 询问从点 u 到点 v 的路径上的节点的最大权值。
III. QSUM u v: 询问从点 u 到点 v 的路径上的节点的权值和。
注意:从点 u 到点 v 的路径上的节点包括 u 和 v 本身。
输入格式
输入文件的第一行为一个整数 n,表示节点的个数。
接下来 n-1 行,每行 2 个整数 a 和 b,表示节点 a 和节点 b 之间有一条边相连。
接下来一行 n 个整数,第 i 个整数 w_i 表示节点 i 的权值。
接下来 1 行,为一个整数 q,表示操作的总数。
接下来 q 行,每行一个操作,以 CHANGE u t 或者 QMAX u v 或者 QSUM u v 的形式给出。
输出格式
对于每个 QMAX 或者 QSUM 的操作,每行输出一个整数表示要求输出的结果。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 2e5 + 10;
#define INF 0x7fffffff
int n, q;
struct node{
int to, nxt;
}e[maxn * 2];
struct Node{
int sum, num;
}ed[maxn * 4];
int head[maxn], cnt, tot, son[maxn], a[maxn], fa[maxn];
int size[maxn], dep[maxn], top[maxn], id[maxn], ran[maxn];
inline void add(int u, int v) {
e[++cnt].nxt = head[u];
e[cnt].to = v;
head[u] = cnt;
}
inline void dfs1(int x, int fat) {
size[x] = 1;
for (int i = head[x]; i; i = e[i].nxt) {
int v = e[i].to;
if (v == fat) continue;
fa[v] = x;
dep[v] = dep[x] + 1;
dfs1(v, x);
size[x] += size[v];
if (size[v] > size[son[x]]) son[x] = v;
}
}
inline void dfs2(int u, int t) {
top[u] = t; id[u] = ++tot; ran[tot] = u;
if (!son[u]) return;
dfs2(son[u], t);
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (v != son[u] && v != fa[u]) dfs2(v, v);
}
return;
}
inline void push_up(int x) {
ed[x].sum = ed[x << 1].sum + ed[x << 1 | 1].sum;
ed[x].num = max(ed[x << 1].num, ed[x << 1 | 1].num);
}
inline void build(int now, int l, int r) {
if (l == r) {
ed[now].sum = a[ran[l]];
ed[now].num = a[ran[l]];
return;
}
int mid = (l + r) >> 1;
build(now << 1, l, mid);
build(now << 1 | 1, mid + 1, r);
push_up(now);
}
inline void update(int now, int l, int r, int x, int y) {
int mid = (l + r) >> 1;
if (l == r) {
ed[now].sum = y;
ed[now].num = y;
return;
}
if (x <= mid) update(now << 1, l, mid, x, y);
else update(now << 1 | 1, mid + 1, r, x, y);
push_up(now);
}
inline int querymax(int now, int left, int right, int l, int r) {
if (l <= left && r >= right) return ed[now].num;
int mid = (left + right) >> 1;
int ans = -INF;
if (mid >= l) ans = max(ans, querymax(now << 1, left, mid, l, r));
if (mid < r) ans = max(ans, querymax(now << 1 | 1, mid + 1, right, l, r));
return ans;
}
inline int querysum(int now, int left, int right, int l, int r) {
if (l <= left && r >= right) return ed[now].sum;
int mid = (left + right) >> 1;
int ans = 0;
if (mid >= l) ans += querysum(now << 1, left, mid, l, r);
if (mid < r) ans += querysum(now << 1 | 1, mid + 1, right, l, r);
return ans;
}
inline int query1(int x, int y) {
int ans = -INF;
int fax = top[x], fay = top[y];
while (fax != fay) {
if (dep[fax] < dep[fay]) {
swap(x, y); swap(fax, fay);
}
ans = max(ans, querymax(1, 1, tot, id[fax], id[x]));
x = fa[fax]; fax = top[x];
}
if (id[x] > id[y]) swap(x, y);
ans = max(ans, querymax(1, 1, tot, id[x], id[y]));
return ans;
}
inline int query2(int x, int y) {
int ans = 0;
int fax = top[x], fay = top[y];
while (fax != fay) {
if (dep[fax] < dep[fay]) {
swap(x, y); swap(fax, fay);
}
ans += querysum(1, 1, tot, id[fax], id[x]);
x = fa[fax]; fax = top[x];
}
if (id[x] > id[y]) swap(x, y);
ans += querysum(1, 1, tot, id[x], id[y]);
return ans;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n;
for (int i = 1; i < n; i++) {
register int u, v;
cin >> u >> v;
add(u, v); add(v, u);
}
for (int i = 1; i <= n; i++) cin >> a[i];
dfs1(1, 0); dfs2(1, 1);
//cout << "step1 over" << endl;
build(1, 1, n);
cin >> q;
while (q--) {
char s[10]; register int x, y;
cin >> s >> x >> y;
if (s[0] == 'C') update(1, 1, n, id[x], y);
else if (s[1] == 'M') cout << query1(x, y) << endl;
else cout << query2(x, y) << endl;
}
return 0;
}
题目描述
如题,已知一棵包含 NN 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
1 x y z,表示将树从 x 到 y 结点最短路径上所有节点的值都加上 z。
2 x y,表示求树从 x 到 y 结点最短路径上所有节点的值之和。
3 x z,表示将以 x 为根节点的子树内所有节点值都加上 z。
4 x 表示求以 x 为根节点的子树内所有节点值之和
输入格式
第一行包含 44 个正整数 N,M,R,P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含 N 个非负整数,分别依次表示各个节点上初始的数值。
接下来 N-1 行每行包含两个整数 x,y,表示点 x 和点 y 之间连有一条边(保证无环且连通)。
接下来 M 行每行包含若干个正整数,每行表示一个操作。
输出格式
输出包含若干行,分别依次表示每个操作 2 或操作 4 所得的结果(对 P 取模)。
代码是几个月前写的了,忘了当时跟着哪篇博客写的,有些地方不太一样,不过套路是一样的
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 1e7 + 10;
const int maxm = 1e4 + 10;
struct node{
int nxt, to;
}e[maxn];
struct edge{
int sum, lazy, l, r;
}ed[maxn];
int n, m, cnt, tot, root, mod, a[maxn], head[maxn];
int fa[maxn], ch[maxn], dep[maxn], size[maxn], son[maxn], rank[maxn], top[maxn], id[maxn];
inline int read() {
int x = 0, k = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') k = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * k;
}
inline void build(int now, int l, int r) {
if (l == r) {
ed[now].sum = a[l];
return;
}
int mid = (l + r) >> 1;
build(now << 1, l, mid);
build(now << 1 | 1, mid + 1, r);
ed[now].sum = (ed[now << 1].sum + ed[now << 1 | 1].sum) % mod;
return;
}
inline void pushdown(int now, int l, int r) {
int mid = (l + r) >> 1;
ed[now << 1].lazy += ed[now].lazy;
ed[now << 1].lazy %= mod;
ed[now << 1 | 1].lazy += ed[now].lazy;
ed[now << 1 | 1].lazy %= mod;
ed[now << 1].sum += ed[now].lazy * (mid - l + 1);
ed[now << 1].sum %= mod;
ed[now << 1 | 1].sum += ed[now].lazy * (r - mid);
ed[now << 1 | 1].sum %= mod;
ed[now].lazy = 0;
return;
}
inline void update(int now, int left, int right, int l, int r, int k) {
if (l <= left && r >= right) {
ed[now].sum += k * (right - left + 1);
ed[now].sum %= mod;
ed[now].lazy += k;
ed[now].lazy %= mod;
return;
}
if (left > r || right < l) return;
int mid = (left + right) >> 1;
if (ed[now].lazy) pushdown(now, left, right);
if (mid >= l) update(now << 1, left, mid, l, r, k);
if (mid < r) update(now << 1 | 1, mid + 1, right, l, r, k);
ed[now].sum = (ed[now << 1].sum + ed[now << 1 | 1].sum) % mod;
return;
}
inline int query(int now, int left, int right, int l, int r) {
if (l <= left && r >= right) return ed[now].sum % mod;
if (left > r || right < l) return 0;
int mid = (left + right) >> 1;
if (ed[now].lazy) pushdown(now, left, right);
int num1 = 0, num2 = 0;
if (mid >= l) num1 = query(now << 1, left, mid, l, r);
if (mid < r) num2 = query(now << 1 | 1, mid + 1, right, l, r);
num1 %= mod; num2 %= mod;
return (num1 + num2) % mod;
}
inline void add(int u, int v) {
e[++cnt].nxt = head[u];
e[cnt].to = v;
head[u] = cnt;
}
inline void dfs1(int x) {
size[x] = 1;
for (int i = head[x]; i; i = e[i].nxt) {
int v = e[i].to;
if (!dep[v]) {
dep[v] = dep[x] + 1;
fa[v] = x;
dfs1(v);
size[x] += size[v];
if (size[v] > size[son[x]]) son[x] = v;
}
}
}
inline void dfs2(int u, int t) {
top[u] = t; id[u] = ++tot; a[tot] = ch[u];
if (!son[u]) return;
dfs2(son[u], t);
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (v != son[u] && v != fa[u]) dfs2(v, v);
}
return;
}
inline int cal1(int x, int y) {
int ans = 0;
int fax = top[x], fay = top[y];
while (fax != fay) {
if (dep[fax] < dep[fay]) {
swap(x, y); swap(fax, fay);
}
ans += query(1, 1, tot, id[fax], id[x]);
x = fa[fax]; fax = top[x];
}
if (id[x] > id[y]) swap(x, y);
ans += query(1, 1, tot, id[x], id[y]);
return ans;
}
inline void cal2(int x, int y, int v) {
int fax = top[x], fay = top[y];
while (fax != fay) {
if (dep[fax] < dep[fay]) {
swap(x, y); swap(fax, fay);
}
update(1, 1, tot, id[fax], id[x], v);
x = fa[fax]; fax = top[x];
}
if (id[x] > id[y]) swap(x, y);
update(1, 1, tot, id[x], id[y], v);
}
int main() {
n = read(); m = read(); root = read(); mod = read();
for (int i = 1; i <= n; i++) {
ch[i] = read(); ch[i] %= mod;
}
for (int i = 1; i < n; i++) {
register int u, v;
u = read(); v = read();
add(u, v); add(v, u);
}
dep[root] = 1; fa[root] = 1;
dfs1(root); dfs2(root, root);
build(1, 1, n);
while (m--) {
register int op; op = read();
if (op == 1) {
register int u, v, w;
u = read(); v = read(); w = read();
cal2(u, v, w % mod);
} else if (op == 2) {
register int u, v;
u = read(); v = read();
printf("%d\n", cal1(u, v) % mod);
} else if (op == 3) {
register int u, v;
u = read(); v = read();
update(1, 1, n, id[u], id[u] + size[u] - 1, v % mod);
} else if (op == 4) {
register int u; u = read();
printf("%d\n", query(1, 1, n, id[u], id[u] + size[u] - 1) % mod);
}
}
return 0;
}
题目背景
Linux 用户和 OSX 用户一定对软件包管理器不会陌生。通过软件包管理器,你可以通过一行命令安装某一个软件包,然后软件包管理器会帮助你从软件源下载软件包,同时自动解决所有的依赖(即下载安装这个软件包的安装所依赖的其它软件包),完成所有的配置。Debian/Ubuntu 使用的 apt-get,Fedora/CentOS 使用的 yum,以及 OSX 下可用的 homebrew 都是优秀的软件包管理器。
题目描述
你决定设计你自己的软件包管理器。不可避免地,你要解决软件包之间的依赖问题。如果软件包 a 依赖软件包 b,那么安装软件包 a 以前,必须先安装软件包 b。同时,如果想要卸载软件包 b,则必须卸载软件包 a。
现在你已经获得了所有的软件包之间的依赖关系。而且,由于你之前的工作,除 0 号软件包以外,在你的管理器当中的软件包都会依赖一个且仅一个软件包,而 0 号软件包不依赖任何一个软件包。且依赖关系不存在环(即不会存在 m 个软件包 a_1, a_2, a_3..., a_m, 对于 i<m,a_i 依赖 a_i+1,而 a_m 依赖 a_1 的情况)。
现在你要为你的软件包管理器写一个依赖解决程序。根据反馈,用户希望在安装和卸载某个软件包时,快速地知道这个操作实际上会改变多少个软件包的安装状态(即安装操作会安装多少个未安装的软件包,或卸载操作会卸载多少个已安装的软件包),你的任务就是实现这个部分。
注意,安装一个已安装的软件包,或卸载一个未安装的软件包,都不会改变任何软件包的安装状态,即在此情况下,改变安装状态的软件包数为 0。
输入格式
第一行一个正整数 n,表示软件包个数,从 0 开始编号。
第二行有 n-1 个整数,第 i 个表示 i 号软件包依赖的软件包编号。
然后一行一个正整数 q,表示操作个数,格式如下:
install x 表示安装 x 号软件包
uninstall x 表示卸载 x 号软件包
一开始所有软件包都是未安装的。
对于每个操作,你需要输出这步操作会改变多少个软件包的安装状态,随后应用这个操作(即改变你维护的安装状态)。
输出格式
输出 q 行,每行一个整数,表示每次询问的答案。
首先,我们可以将所有的软件看作一棵树,初始时都是 -1
对于安装操作,相当于将它到根节点的路径上的点全都变为 1
对于卸载操作,相当于将它的子树全都变为 0
然后只要输出每次操作前后整棵树权值的变化量即可
卸载操作直接在 dfs 序后的线段树上区间覆盖
安装操作在树剖树上向上走,然后不断更新路径即可
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 1e7 + 10;
const int maxm = 1e4 + 10;
struct node{
int nxt, to;
}e[maxn];
struct edge{
int sum, lazy, l, r;
}ed[maxn];
int n, m, cnt, tot, head[maxn];
int fa[maxn], dep[maxn], rank[maxn], size[maxn], son[maxn], top[maxn], id[maxn];
inline int read() {
int x = 0, k = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') k = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * k;
}
inline void build(int now, int l, int r) {
ed[now].l = l; ed[now].r = r;
if (l == r) {
ed[now].sum = 0;
ed[now].lazy = -1;
return;
}
int mid = (l + r) >> 1;
build(now << 1, l, mid);
build(now << 1 | 1, mid + 1, r);
}
inline void pushdown(int now) {
if (~ed[now].lazy) {
int lc = now << 1, rc = (now << 1) + 1;
ed[lc].sum = ed[now].lazy * (ed[lc].r - ed[lc].l + 1), ed[lc].sum;
ed[rc].sum = ed[now].lazy * (ed[rc].r - ed[rc].l + 1), ed[rc].sum;
ed[lc].lazy = ed[now].lazy;
ed[rc].lazy = ed[now].lazy;
ed[now].lazy = -1;
}
}
inline void update(int now, int l, int r, int k) {
if (l <= ed[now].l && ed[now].r <= r) {
ed[now].sum = k * (ed[now].r - ed[now].l + 1);
ed[now].lazy = k;
return;
}
int mid = (ed[now].l + ed[now].r) >> 1;
pushdown(now);
if (l <= mid) update(now << 1, l, r, k);
if (r > mid) update(now << 1 | 1, l, r, k);
ed[now].sum = ed[now << 1].sum + ed[now << 1 | 1].sum;
}
inline void change(int x, int y, int v) {
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) swap(x, y);
update(1, id[top[x]], id[x], v);
x = fa[top[x]];
}
if (dep[x] > dep[y]) swap(x, y);
update(1, id[x], id[y], v);
}
inline void add(int u, int v) {
e[++cnt].nxt = head[u];
e[cnt].to = v;
head[u] = cnt;
}
inline void dfs1(int x) {
size[x] = 1; dep[x] = dep[fa[x]] + 1;
for (int i = head[x]; i; i = e[i].nxt) {
int v = e[i].to;
if (v != fa[x]) {
fa[v] = x;
dfs1(v);
size[x] += size[v];
if (!son[x]||size[v] > size[son[x]]) son[x] = v;
}
}
}
inline void dfs2(int x) {
if (!top[x]) top[x] = x;
id[x] = ++tot; rank[tot] = x;
if (son[x]) top[son[x]] = top[x], dfs2(son[x]);
for (int i = head[x]; i; i = e[i].nxt) {
int v = e[i].to;
if (v != son[x] && v != fa[x]) dfs2(v);
}
}
int main() {
n = read();
for (int i = 2; i <= n; i++) {
register int x;
x = read();
x++;
add(x, i);
}
dfs1(1);
dfs2(1);
build(1, 1, n);
m = read();
while (m--) {
string s;
register int x;
cin >> s >> x;
x++;
int bef = ed[1].sum;
if (s == "install") {
change(1, x ,1);
int aft = ed[1].sum;
cout << abs(bef - aft) << endl;
} else {
update(1, id[x], id[x] + size[x] - 1, 0);
int aft = ed[1].sum;
cout << abs(bef - aft) << endl;
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号