2021牛客寒假算法基础集训营1部分题目题解
题解顺序按照通过人数排序,难度递增
比赛这次是真的参加了,然后就...死了,数学菜狗在线自闭
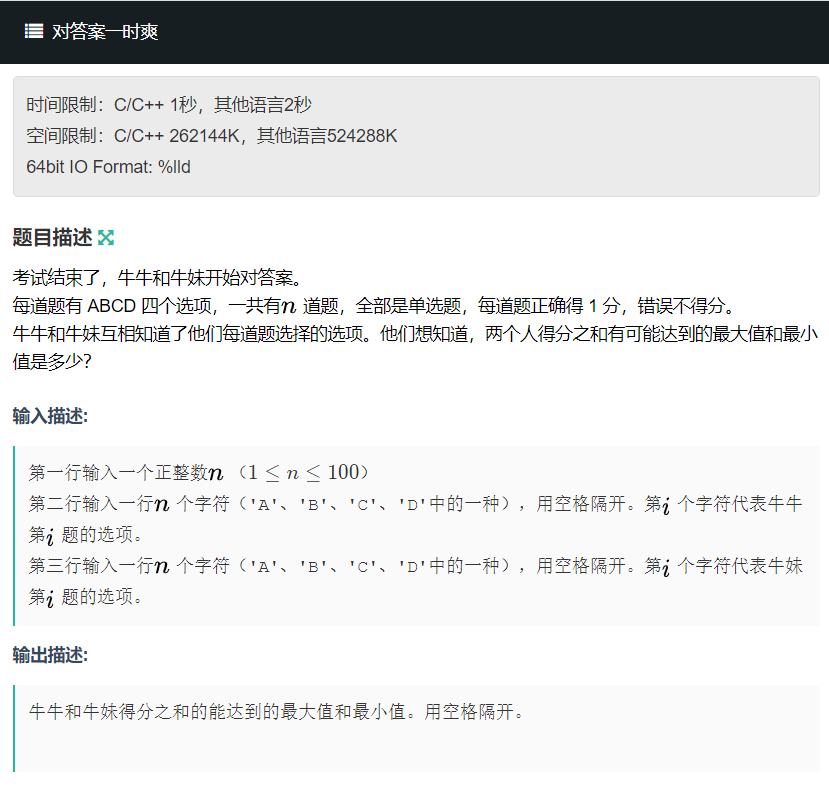
F 对答案一时爽
签到题
示例1
输入
1
B
A
输出
1 0
说明
若正确答案为 A,那么牛牛分数是 0,牛妹分数是 1,得分之和为 0+1=1。
若正确答案为 B,那么牛牛分数是 1,牛妹分数是 0,得分之和为 1+0=1。
若正确答案为 C,那么牛牛分数是 0,牛妹分数是 0,得分之和为 0+0=0。
若正确答案为 D,那么牛牛分数是 0,牛妹分数是 0,得分之和为 0+0=0。
所以他们得分之和的最大值是 1 ,最小值是 0
示例2
输入
3
C A C
B D B
输出
3 0
原谅我身为数学弱智连这题都要反应半天
最小得分的情况其实很好想,无论怎么样最小得分都是0,那么最大得分呢,那就只需要让牛牛(或者牛妹)的答案全对,再统计另一个人的答案有多少是和此人一样的,然后两者加起来就可以
#include <bits/stdc++.h>
#define rep(i, x, y) for (int i = x; i <= y; i++)
#define dep(i, x, y) for (int i = x; i >= y; i--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int INF = 1e9;
const int maxn = 1e7 + 10;
const int maxm = 1e4 + 10;
int n, ans, ans1;
char a[maxn], b[maxn];
inline ll read() {
ll x = 0, k = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') k = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * k;
}
int main() {
n = read();
rep(i, 1, n) cin >> a[i];
getchar();
rep(i, 1, n) cin >> b[i];
rep(i, 1, n) if (a[i] == b[i]) ans++;
ans1 = ans + n;
printf("%d %d", ans1, 0);
return 0;
}
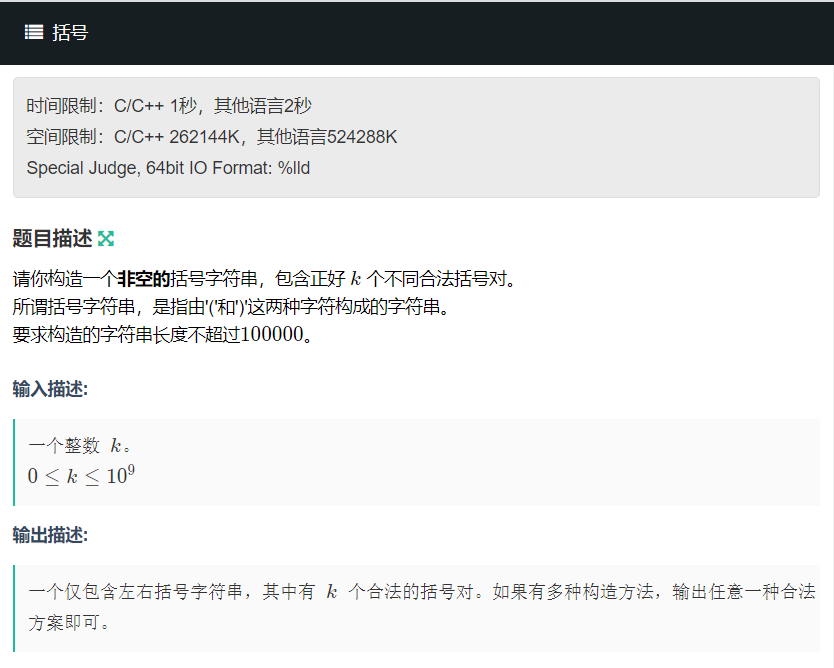
B 括号
构造题
示例1
输入
3
输出
()()
说明
假设字符串数组下标从 1 开始,则 (1,2), (1,4), (3,4) 共计 3 个合法括号对
当然,"()))" 也是一种合法的构造
示例2
输入
4
输出
(())
说明
假设字符串数组下标从 1 开始,则 (1,3), (1,4), (2,3), (2,4) 共计 4 个合法括号对
另外,合法的构造还有"())()"、"()(()(" 等等。。
身为渣渣这题困了我两个小时......后来突然灵机一动才A了这题
首先就是另 num = sqrt(k),然后画出 num 个“(”, num个“)”,k -= num * 2,之后如果 k - num >= 0 的话就不断执行 k -= num,每执行一次就在串的末尾加一个“)”,直到最后 k 剩余的值小于 num 了,这样的话就可以在第 k 个“(”的后面跟一个“)”,那么就可以完成我们的构造了
#include <bits/stdc++.h>
#define rep(i, x, y) for (int i = x; i <= y; i++)
#define dep(i, x, y) for (int i = x; i >= y; i--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int INF = 1e9;
const int maxn = 1e7 + 10;
const int maxm = 1e4 + 10;
int k, cnt, tot;
char a[maxn];
inline ll read() {
ll x = 0, k = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') k = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * k;
}
int main() {
k = read();
if (k == 0) {
cout << "(";
return 0;
}
if (k == 1) {
cout << "()";
return 0;
}
if (k == 2) {
cout << "())";
return 0;
}
if (k == 3) {
cout << "()()";
return 0;
}
int num = sqrt(k);
rep(i, 1, num) a[i] = '(';
rep(i, num + 1, 2 * num) a[i] = ')';
int cnt = 2 * num;
k -= num * num;
while (k - num >= 0) {
a[++cnt] = ')';
k -= num;
}
rep(i, 1, cnt) {
cout << a[i];
if (i == k) cout << ')';
}
return 0;
}
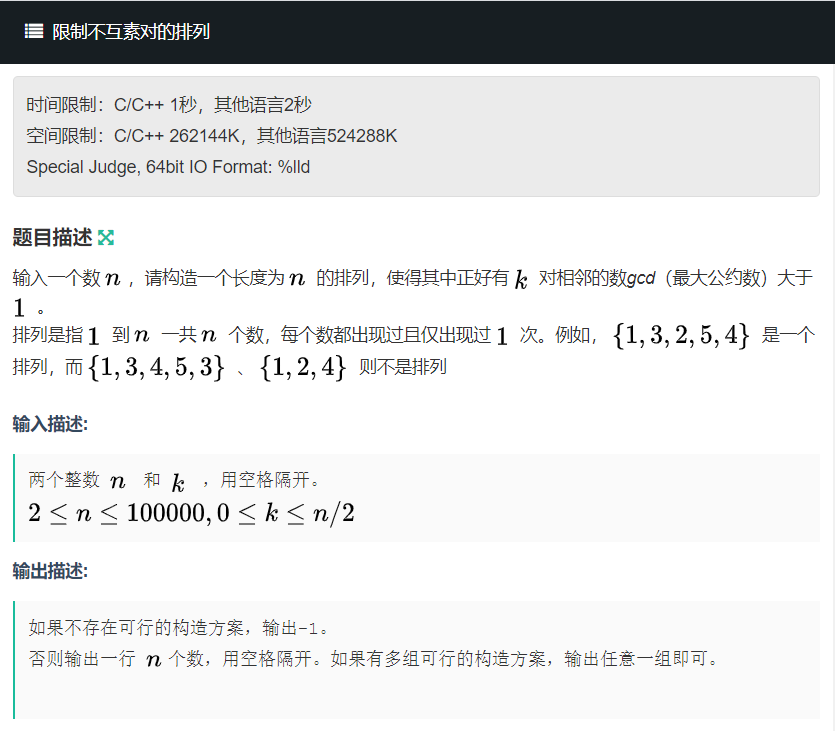
I 限制不互素对的排列
构造
示例1
输入
2 1
输出
-1
说明
长度为2的排列有2个:{1,2}和{2,1},显然都不符合题意
示例2
输入
6 3
输出
5 3 6 2 4 1
说明
共有3对相邻数不互素:{3,6}、{6,2}和{2,4}。
这并不是唯一解,只要构造任意合法解即可。
可以知道,大于等于2的相邻两数都互素,相邻的奇数也互素
如果把所有的偶数都放一起,奇数都放一起(从小到大),偶数们都不互素((n / 2 - 1)对),奇数们都互素
1、如果 k <= n / 2 - 1,前面放 k 对偶数组,即2,4,6,8...,然后接与最后一个偶数相邻的奇数再不断加一,最后把剩下的小的放在最后面就可以了
例:2,4,6,8,10,12,13,14,15,16,17...25,1,3,5,7,9,11
2、如果k = n / 2,那么就代表这堆偶数是不够用的,那么就需要再来一对,很容易想到3、6,即偶数是6结尾,奇数用3开头,其他顺着来
#include <bits/stdc++.h>
#define rep(i, x, y) for (int i = x; i <= y; i++)
#define dep(i, x, y) for (int i = x; i >= y; i--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int INF = 1e9;
const int maxn = 1e7 + 10;
const int maxm = 2e5 + 10;
int n, k, vis[maxn];
inline ll read() {
ll x = 0, k = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') k = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * k;
}
int main() {
n = read(); k = read();
if (k == n / 2) {
if (n >= 6) {
printf("3 6");
for (int i = 1; i * 2 <= n; i++) {
if (i * 2 == 6) continue;
printf(" %d", i * 2);
}
for (int i = 1; i <= n; i += 2) {
if (i == 3) continue;
printf(" %d", i);
}
printf("\n");
}
else printf("-1\n");
}
else {
rep(i, 1, k + 1) {
printf("%d", 2 * i);
vis[2 * i] = 1;
if (i != k + 1) printf(" ");
}
rep(i, 1, n) if (!vis[i]) printf(" %d", i);
}
return 0;
}
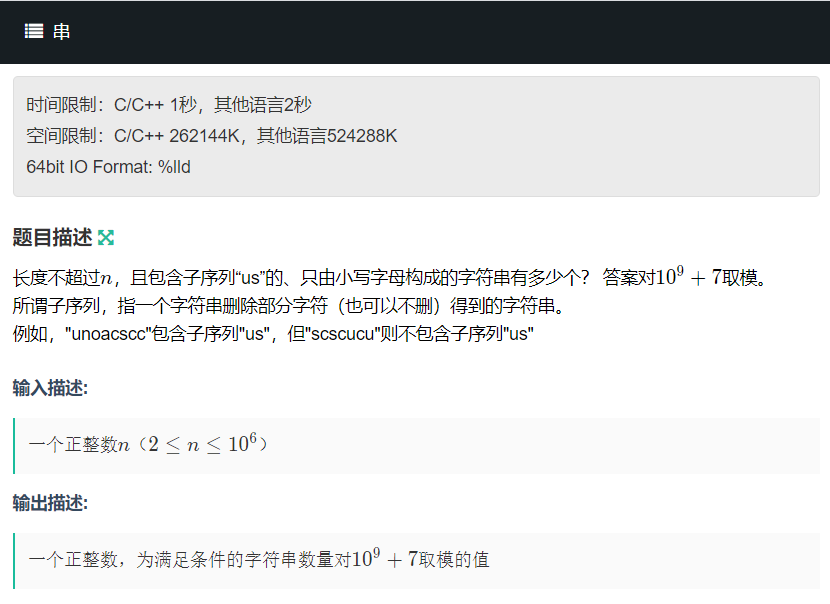
A 串
dp
示例1
输入
2
输出
1
说明
仅有“us”这一个字符串合法
示例2
输入
3
输出
77
说明
长度为3的字符串里,
形状是"u?s"的共有26个
形状是"?us"的共有26个
形状是"us?"的共有26个。
但是,"uss"和"uus"被各多计算了1次,应该减去,
所以共有26*3-2=76个。
再加上长度为2的"us",所以长度不超过3的合法字符串共有77个。
暴力炸了,这题是dp
我们考虑一个字母一个字母地往已有串后面添加,这样的话可以分为两种情况:
1、前面已经有完整的us了,那么第i个位置随便添加
2、前面没有完整的us但是有u,那么第i个位置我们就只能添加s
使用f[i][0]表示长度为i没有u的,f[i][1]表示有u但u后面没有s的,f[i][2]表示有us的
那么动态转移方程即为:
dp[i][0] = dp[i - 1][0] * 25
dp[i][1] = dp[i - 1][1] * 25 + dp[i - 1][0]
dp[i][2] = dp[i - 1][1] + dp[i - 1][2] * 26
#include <bits/stdc++.h>
#define rep(i, x, y) for (int i = x; i <= y; i++)
#define dep(i, x, y) for (int i = x; i >= y; i--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int INF = 1e9;
const int maxn = 1e7 + 10;
const int maxm = 1e4 + 10;
const ll mod = 1e9 + 7;
ll n, dp[maxn][3], ans;
inline ll read() {
ll x = 0, k = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') k = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * k;
}
int main() {
n = read();
dp[0][0] = 1;
rep(i, 1, n) {
dp[i][0] = dp[i - 1][0] * 25 % mod;
dp[i][1] = (dp[i - 1][1] * 25 % mod + dp[i - 1][0]) % mod;
dp[i][2] = (dp[i - 1][1] + dp[i - 1][2] * 26 % mod) % mod;
}
rep(i, 1, n) ans = (ans + dp[i][2]) % mod;
printf("%lld\n", ans);
return 0;
}
J 一群小青蛙呱嘣呱嘣呱

输入
7
输出
6
说明
数字 1 可以被所有青蛙吃掉;
数字 2 可以被第 1 只青蛙吃掉;
数字 3 可以被第 2 只青蛙吃掉;
数字 4 可以被第 1 只青蛙吃掉;
数字 5 可以被第 3 只青蛙吃掉;
数字 6 无法被吃掉;
数字 7 可以被第 4 只青蛙吃掉。
所以剩下的数字只有一个 6 ,所有数的 lcm 为 6
数学公式太难打了,直接把雨巨写的整上来吧

#include <bits/stdc++.h>
#define rep(i, x, y) for (int i = x; i <= y; i++)
#define dep(i, x, y) for (int i = x; i >= y; i--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll mod = 1e9 + 7;
const int maxn = 80000010;
int n, cnt, vis[maxn], a[maxn];
inline ll read() {
ll x = 0, k = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') k = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * k;
}
inline void work(int n) {
rep(i, 2, n) {
if (!a[i]) vis[cnt++] = i;
for (int j = 0; vis[j] <= n / i; j++) {
a[vis[j] * i] = 1;
if (i % vis[j] == 0) break;
}
}
}
int main() {
n = read();
work(n / 2);
if (n < 6) {
printf("empty\n");
return 0;
}
ll ans = 1;
for (int i = 0; i < cnt; i++) {
ll mid = 2, now = 1;
if (i == 0) mid = 3;
while (now * vis[i] <= n / mid) now *= vis[i];
ans *= now;
ans %= mod;
}
printf("%lld\n", ans);
return 0;
}
E 三棱锥之刻

输入
1 1
输出
1.73205
说明
正三棱锥棱长为 1 ,且喷雾的有效射程为 1 ,易知牛牛可以将喷雾喷满整个内表面,即结果为整个内表面的面积。
这是一道数学题,不会数学的我怎么可能会做呢,赛后整的别人的
#include <bits/stdc++.h>
#define rep(i, x, y) for (int i = x; i <= y; i++)
#define dep(i, x, y) for (int i = x; i >= y; i--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define INF 0x7fffffff
const int mod = 1e9 + 7;
const int maxn = 1e7 + 10;
const int maxm = 2e5 + 10;
const double PI = acos(-1.0);
double a, r;
inline ll read() {
ll x = 0, k = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') k = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * k;
}
int main() {
cin >> a >> r;
double h = sqrt(6.0) / 12.0 * a;
if (h >= r) {
printf("0\n");
return 0;
}
double l = sqrt(r * r - h * h);
double co = sqrt(3.0) / 6.0 * a;
double jia;
if (l <= co) {
printf("%.10f\n", 4 * PI * l * l);
return 0;
}
else jia = acos(co / l);
if (jia >= PI / 3.0) printf("%.10f\n", 4 * co * a / 2 * 3);
else printf("%.10f\n", 4 * (l * l * (2 * PI - 6 * jia) / 2 + 3 * (co * l * sin(jia))));
return 0;
}
D 点一成零

示例
输入
3
100
001
000
3
0 1
1 1
1 2
输出
4
4
4
说明
将第0行第1列的数变成1之后,方阵变成了这样:
110
001
000
一共有3个1。假设行号作为x轴坐标,列号作为y轴坐标,设坐标为(0,0)的是1号,坐标为(0,1)的是2号,坐标为(1,2)的是3号。
那么共有以下四种方案:
1->3
2->3
3->1
3->2
所以输出4。
将第1行第1列的数变成1之后,方阵变成了这样:
110
011
000
一共有4个1,显然它们是连通的,只要选择任意一个1,那么就全部变成0了,所以是4种方案。
将第1行第2列的数变成1,方阵不会有任何改变:
110
011
000
所以方案数依然为4。
懒得打字了,直接把官方题解整上来了

#include <bits/stdc++.h>
#define rep(i, x, y) for (int i = x; i <= y; i++)
#define dep(i, x, y) for (int i = x; i >= y; i--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define INF 0x7fffffff
const ll mod = 1000000007;
const int maxn = 1e7 + 10;
const int maxm = 1e4 + 10;
const int dx[4] = {-1, 0, 1, 0};
const int dy[4] = {0, -1, 0, 1};
int f[maxm][maxm], g[maxm][maxm];
int n, num, fa[maxn], s[maxn];
ll ans = 1, inv[maxn], sum;
char str[maxn];
inline void init() {
rep(i, 1, 10000000) fa[i] = i;
}
inline void build() {
inv[1] = 1;
rep(i, 2, 300000)
inv[i] = (mod - mod / i) * inv[mod % i] % mod;
}
inline int find(int x) {
if (fa[x] == x) return x;
return fa[x] = find(fa[x]);
}
inline void merge(int x, int y) {
int xx = find(x), yy = find(y);
if (xx == yy) return;
ans = (ans * inv[s[xx]]) % mod;
ans = (ans * inv[s[yy]]) % mod;
ans = (ans * inv[sum]) % mod;
fa[yy] = xx;
s[xx] += s[yy];
s[yy] = 0;
ans = (ans * s[xx]) % mod;
sum--;
}
int main() {
scanf("%d", &n);
build();
rep(i, 1 ,n) {
scanf("%s", str + 1);
rep(j, 1, n) {
g[i][j] = ++num;
if (str[j] == '1') {
f[i][j] = 1;
s[g[i][j]] = 1;
sum++;
ans = ans * sum % mod;
}
}
}
init();
rep(i, 1, n)
rep(j, 1, n) {
if (f[i][j] == 0) continue;
if (i != 1 && f[i - 1][j] == 1)
merge(g[i][j], g[i - 1][j]);
if (j != 1 && f[i][j - 1] == 1)
merge(g[i][j], g[i][j - 1]);
}
int t, a, b;
scanf("%d", &t);
while (t--) {
scanf("%d%d", &a, &b);
a++; b++;
if (f[a][b] == 1) {
printf("%lld\n", ans);
continue;
}
f[a][b] = 1; s[g[a][b]] = 1;
sum++; ans = ans * sum % mod;
for (int k = 0, aa, bb; k < 4; k++) {
aa = a + dx[k];
bb = b + dy[k];
if (aa < 1 || aa > n || bb < 1 || bb > n || f[aa][bb] == 0) continue;
merge(g[a][b], g[aa][bb]);
}
printf("%lld\n", ans);
}
return 0;
}
剩下的暂时先不写了,CTF那边最近有点忙...


 浙公网安备 33010602011771号
浙公网安备 33010602011771号