最小生成树/次小生成树/Kruskal重构树学习笔记
参考博客(侵删):
勿在浮沙筑高台-算法导论--最小生成树(Kruskal和Prim算法)
最近做了一下洛谷最小生成树的题单,把三种问题整理到这里方便今后查看
最小生成树
关于图的几个概念定义:
- 连通图:在无向图中,若任意两个顶点vi与vj都有路径相通,则称该无向图为连通图。
- 强连通图:在有向图中,若任意两个顶点vi与vj都有路径相通,则称该有向图为强连通图。
- 连通网:在连通图中,若图的边具有一定的意义,每一条边都对应着一个数,称为权;权代表着连接连个顶点的代价,称这种连通图叫做连通网。
- 生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
- 最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。
1、Kruskal算法
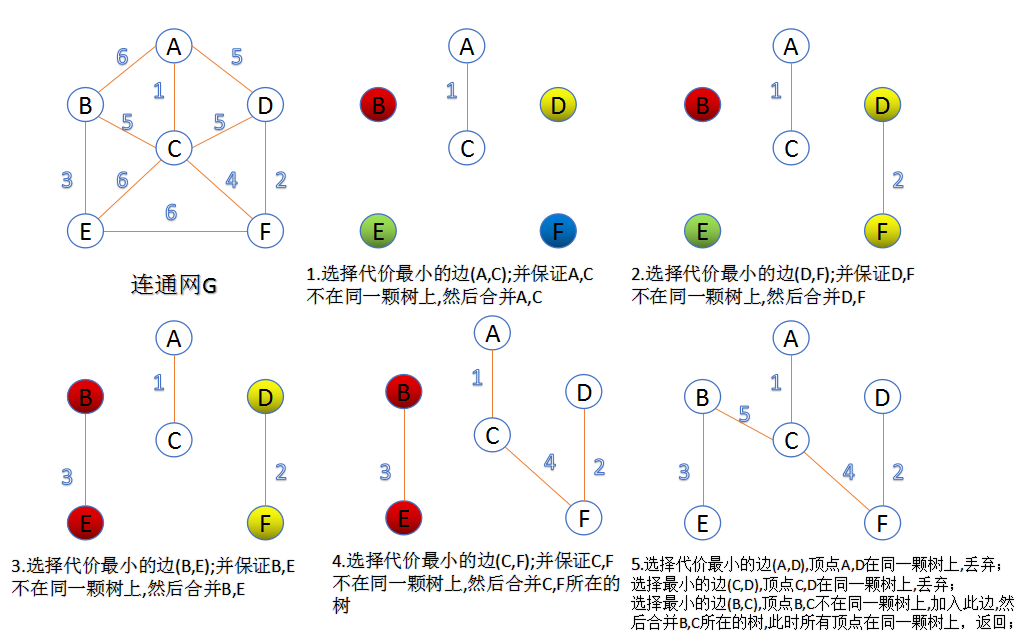
此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。
-
把图中的所有边按代价从小到大排序;
-
把图中的n个顶点看成独立的n棵树组成的森林;
-
按权值从小到大选择边,所选的边连接的两个顶点ui,vi,应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
-
重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <queue>
#define ll long long
#define INF 0x7fffffff
using namespace std;
const int maxn = 1e7 + 10;
int n, m, cnt, ans, fa[maxn];
struct node{
int u, v, len;
}e[maxn];
inline ll read() {
ll x = 0, k = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') k = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * k;
}
inline void add(int x, int y, int z) {
e[++cnt].u = x;
e[cnt].v = y;
if (z != 0) e[cnt].len = z;
else e[cnt].len = INF;
}
inline bool cmp(node x, node y) {
return x.len < y.len;
}
inline void init() {
for (int i = 1; i <= m; i++) fa[i] = i;
}
inline int find(int x) {
if (fa[x] == x) return x;
return fa[x] = find(fa[x]);
}
inline void kruskal() {
int i = 0, sum = 0;
while (i <= cnt && sum <= m) {
if (find(e[i].u) != find(e[i].v)) {
sum++;
ans += e[i].len;
fa[find(e[i].u)] = find(e[i].v);
}
i++;
}
}
int main() {
n = read(); m = read();
init();
for (int i = 1; i <= m; i++)
for (int j = 1; j <= m; j++) {
register int x; x = read();
if (i < j) add(i, j, x);
}
for (int i = 1; i <= m; i++) add(0, i, n);
sort(e + 1, e + 1 + cnt, cmp);
kruskal();
printf("%d\n", ans);
return 0;
}
2、Prim算法
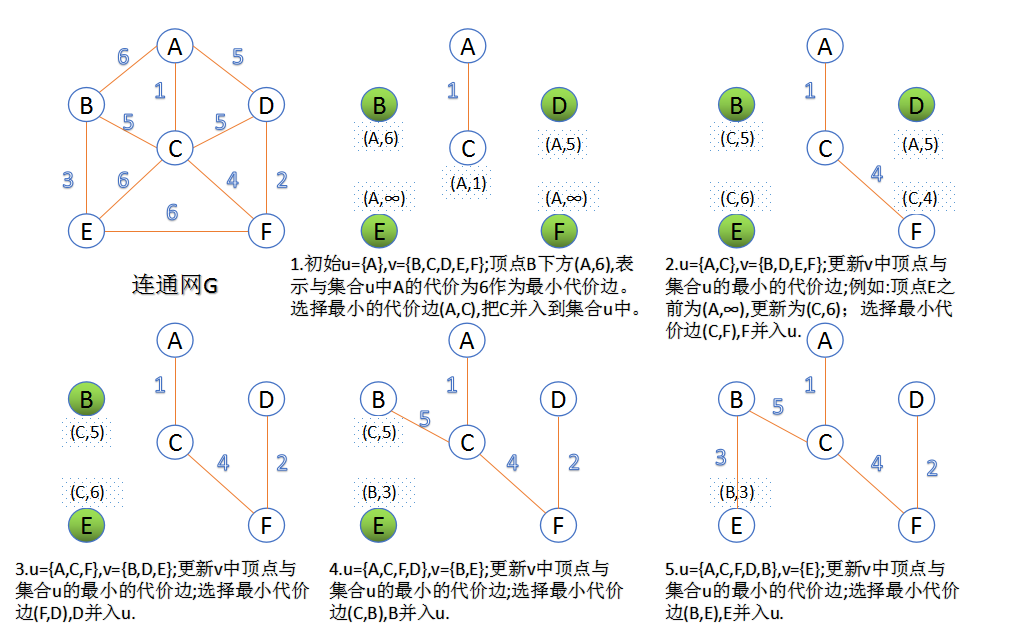
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
1.图的所有顶点集合为V;初始令集合u={s},v=V−u;
2.在两个集合u,v能够组成的边中,选择一条代价最小的边(u0,v0),加入到最小生成树中,并把v0并入到集合u中。
3.重复上述步骤,直到最小生成树有n-1条边或者n个顶点为止。
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <map>
#include <set>
#include <vector>
#include <algorithm>
#define INF 1e7 + 1
using namespace std;
const int maxn = 5001;
int n, m, u, v, w;
int cost[maxn][maxn], mincost[maxn];
bool vis[maxn];
inline void init() {
for (int i = 0; i <= maxn; i++)
for (int j = 0; j <= maxn; j++)
if (i == j) cost[i][j] = 0;
else cost[i][j] = INF;
}
inline int prim() {
for (int i = 0; i < n; ++i) {
mincost[i] = INF;
vis[i] = false;
}
mincost[0] = 0;
int res = 0;
while (1) {
int num = -1;
for (int i = 0; i < n; i++)
if (!vis[i] && (num == -1 || mincost[i] < mincost[num]))
num = i;
if (num == -1) break;
vis[num] = true;
res += mincost[num];
for (int i = 0; i < n; i++)
mincost[i] = min(mincost[i], cost[num][i]);
}
return res;
}
signed main() {
ios::sync_with_stdio(false);
cin >> n >> m;
init();
for (int i = 1; i <= m; i++) {
cin >> u >> v >> w;
cost[u - 1][v - 1] = min(cost[u - 1][v - 1], w);
cost[v - 1][u - 1] = min(cost[u - 1][v - 1], w);
}
cout << prim() << endl;
return 0;
}
次小生成树
次小生成树顾名思义就是次小生成树...
当我们建出了一棵最小生成树,满足使用的边都是最小的,这时候如果我们加入一条非树边,删除最小生成树中的一条边,次小生成树一定是包括在以这种方法建出的树中,注意:一定是删除环中最大的边,这样才保证新生成的树与原来的树相差最小,才可能为次小生成树,所以说问题就转化成了:寻找树上某条路径上的最大边。所以我们就可以使用树上的倍增来实现:num[x][i]=max(num[f[x][i-1]]][i-1],num[x][i-1]),num存的是最大路径值。于是求(x,y)的路径最大值就从x跳到lca,从y跳到lca,两者取个max就行。
题目是严格次小生成树,也就是说,新生成的树一定得比最小生成树大,而不是大于等于。如果加入的红边的长度等于删去的边的长度就不行了,于是针对这种情况,我们还要再考虑考虑怎么办。
于是可以这样处理,对于树上的路径,我们不仅维护一个最大边,还维护一个次大边,这样当最大边等于红边时,不可以删最大边了,我们还可以删去次大边。那么在倍增的时候注意一下维护细节就好。
#include <bits/stdc++.h>
#define rep(i, x, y) for (int i = x; i <= y; i++)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int INF = 1e9;
const int maxn = 1e7 + 10;
const int maxm = 1e4 + 10;
ll n, m, tot, minn = INF, ans, cnt;
ll f[100001][22], num[100001][22], g[100001][22];
ll fa[maxn], head[maxn], dep[maxn];
struct node{
ll x, y, z, flag;
}w[maxn];
struct edge{
ll to, nxt, val;
}e[maxn];
inline ll read() {
ll x = 0, k = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') k = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * k;
}
inline int find(ll x) {
if (fa[x] == x) return x;
return fa[x] = find(fa[x]);
}
inline void add(ll u, ll v, ll z) {
e[++cnt].to = v;
e[cnt].nxt = head[u];
e[cnt].val = z;
head[u] = cnt;
}
inline bool cmp(node a, node b) {
return a.z < b.z;
}
inline void kruskal() {
ll q = 1;
sort(w + 1, w + m + 1, cmp);
rep(i, 1, n) fa[i] = i;
rep(i, 1, m) {
ll xx = find(w[i].x), yy = find(w[i].y);
if (xx != yy) {
ans += w[i].z;
w[i].flag = 1;
q++;
fa[xx] = yy;
add(w[i].x, w[i].y, w[i].z);
add(w[i].y, w[i].x, w[i].z);
}
if (q == n) break;
}
}
inline void dfs(ll x) {
for (int i = head[x]; i; i = e[i].nxt) {
ll v = e[i].to;
if (v == f[x][0]) continue;
f[v][0] = x;
num[v][0] = e[i].val;
dep[v] = dep[x] + 1;
rep(j, 1, 20) {
if (dep[v] < (1 << j)) break;
f[v][j] = f[f[v][j - 1]][j - 1];
num[v][j] = max(num[v][j - 1], num[f[v][j - 1]][j - 1]);
if (num[v][j - 1] == num[f[v][j - 1]][j - 1])
g[v][j] = max(g[v][j - 1], g[f[v][j - 1]][j - 1]);
else {
g[v][j] = min(num[v][j - 1], num[f[v][j - 1]][j - 1]);
g[v][j] = max(g[v][j], g[f[v][j - 1]][j - 1]);
g[v][j] = max(g[v][j - 1], g[v][j]);
}
}
dfs(v);
}
}
inline ll lca(ll u, ll x) {
if (dep[u] < dep[x]) swap(u, x);
for (int i = 20; i >= 0; i--)
if (dep[f[u][i]] >= dep[x]) u = f[u][i];
if (x == u) return x;
for (int i = 20; i >= 0; i--)
if (f[x][i] != f[u][i]) x = f[x][i], u = f[u][i];
return f[x][0];
}
inline void change(ll x, ll y, ll val) {
ll maxx1 = 0, maxx2 = 0;
ll d = dep[x] - dep[y];
rep(i, 0, 20) {
if (d < (1 << i)) break;
if (d & (1 << i)) {
if (num[x][i] > maxx1) {
maxx2 = max(maxx1, g[x][i]);
maxx1 = num[x][i];
}
x = f[x][i];
}
}
if (val != maxx1) minn = min(minn, val - maxx1);
else minn = min(minn, val - maxx2);
}
inline void work() {
rep(i, 1, m)
if (!w[i].flag) {
int xx = w[i].x, yy = w[i].y;
int numm = lca(xx, yy);
change(xx, numm, w[i].z);
change(yy, numm, w[i].z);
}
}
int main() {
n = read(); m = read();
rep(i, 1, m) w[i].x = read(), w[i].y = read(), w[i].z = read();
kruskal();
dfs(1);
work();
printf("%lld\n", ans + minn);
return 0;
}
Kruskal重构树
1、性质
1.是一个小/大根堆(由建树时边权的排序方式决定)
2.LCA(u,v)的权值是 原图 u到v路径上最大/小边权的最小/大值(由建树时边权的排序方式决定)
2、建树
模仿kruskal的过程,先将边权排序 (排序方式决定何种性质接下来说明)
依次遍历每条边
若该边连接的两个节点u和v 不在一个并查集内
就新建一个结点node
该点点权为这条边的边权
找到u,v所在并查集的根ui,vi
连边(node,ui) (node,vi)
并更新并查集fa[ui]=node, fa[vi]=node
遍历完原图所有边后
我们建出来的必定是一棵树
也就是我们要的kruskal重构树
注意这棵树是以最后新建的结点为根的有根树
若原图不连通,即建出的是一个森林
那么就遍历每个节点,找到其并查集的根作为其所在树的根
应用
若我们开始时将边权升序排序
则LCA(u,v)的权值代表 原图 u到v路径上最大边权的最小值
由于边权越大的结点深度越小
所以在这棵树上u到v的路径显然就是原图上u到v尽量沿着边权小的边走
而LCA(u,v)显然就是u到v路径上深度最小的结点
反之若我们一开始将边权降序排序
则LCA(u,v)的权值代表原图u到v路径上最小边权的最大值
#include <bits/stdc++.h>
#define rep(i, x, y) for (int i = x; i <= y; i++)
#define dep(i, x, y) for (int i = x; i >= y; i--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int INF = 1e9;
const int maxn = 1e7 + 10;
const int maxm = 1e4 + 10;
int n, m, q, cnt, tot;
int fa[maxn], val[maxn], size[maxn], vis[maxn];
int top[maxn], dep[maxn], son[maxn], ff[maxn], head[maxn];
struct node{
int u, v, dis;
}e[maxn];
struct edge{
int v, nxt;
}a[maxn];
inline ll read() {
ll x = 0, k = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') k = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * k;
}
inline void add(int u, int v) {
a[++tot].nxt = head[u];
a[tot].v = v;
head[u] = tot;
}
inline int find(int x) {
if (fa[x] == x) return x;
return fa[x] = find(fa[x]);
}
inline bool cmp(node x, node y) {
return x.dis > y.dis;
}
inline void dfs1(int u, int pa) {
size[u] = 1; vis[u] = 1;
for (int i = head[u]; i; i = a[i].nxt) {
int v = a[i].v;
if (v == pa) continue;
dep[v] = dep[u] + 1;
ff[v] = u;
dfs1(v, u);
size[u] += size[v];
if (size[v] > size[son[u]]) son[u] = v;
}
}
inline void dfs2(int u, int tp) {
top[u] = tp;
if (son[u]) dfs2(son[u], tp);
for (int i = head[u]; i; i = a[i].nxt) {
int v = a[i].v;
if (v == son[u] || v == ff[u]) continue;
dfs2(v, v);
}
}
inline void ex_kruskal() {
rep(i, 1, n) fa[i] = i;
sort(e + 1, 1 + e + m, cmp);
rep(i, 1, m) {
int xx = find(e[i].u), yy = find(e[i].v);
if (xx != yy) {
val[++cnt] = e[i].dis;
fa[cnt] = fa[xx] = fa[yy] = cnt;
add(cnt, xx); add(xx, cnt);
add(cnt, yy); add(yy, cnt);
}
}
rep(i, 1, cnt) if (!vis[i]) {
int num = find(i);
dfs1(num, 0); dfs2(num, num);
}
}
inline int lca(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] > dep[top[v]]) u = ff[top[u]];
else v = ff[top[v]];
}
if (dep[u] < dep[v]) return u;
return v;
}
int main() {
n = read(); m = read(); cnt = n;
rep(i, 1, m) e[i].u = read(), e[i].v = read(), e[i].dis = read();
ex_kruskal();
q = read();
while (q--) {
register int x, y;
x = read(); y = read();
if (find(x) != find(y)) printf("-1\n");
else printf("%d\n", val[lca(x, y)]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号