HDU100题简要题解(2050~2059)
HDU2050 折线分割平面
Problem Description
我们看到过很多直线分割平面的题目,今天的这个题目稍微有些变化,我们要求的是n条折线分割平面的最大数目。比如,一条折线可以将平面分成两部分,两条折线最多可以将平面分成7部分,具体如下所示。
Input
输入数据的第一行是一个整数C,表示测试实例的个数,然后是C 行数据,每行包含一个整数n(0<n<=10000),表示折线的数量。
Output
对于每个测试实例,请输出平面的最大分割数,每个实例的输出占一行。
Sample Input
2
1
2
Sample Output
2
7
阿巴阿巴阿巴,是数学题啊
看了大佬的题解才知道该怎么做,接下来详细说一下

根据直线分平面可知,由交点决定了射线和线段的条数,进而决定了新增的区域数。假设第n-1条折线把空间划分为了f[n-1]个部分,那么新增的折线为了使新增空间最多,需要与现有的2 * (n-1)条边都相交。那么新增的线段数为4 * (n-1)[图中黄紫的线],射线数为2[图中绿色的线。每条线段或射线(绿)产生一个新区域,但是折线的头(黄色)的两线段一共只能产生一个区域,所以新增区域的数量为4 * (n-1)-1+2,即 4 * (n-1)+1
故:
f(n)=f(n-1)+4(n-1)+2-1
=f(n-1)+4(n-1)+1
=f(n-2)+4(n-2)+4(n-1)+2
……
=f(1)+4+4*2+……+4(n-1)+(n-1)
=2n^2-n+1
这里附上一篇大佬总结的 各种分平面问题 ,供拓展学习使用
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int n, c;
long long f[10001];
int main() {
while (scanf("%d", &c) != EOF) {
while (c--) {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
f[i] = 2 * n * n - n + 1;
printf("%lld\n", f[n]);
}
}
return 0;
}
HDU2051 Bitset
Problem Description
Give you a number on base ten,you should output it on base two.(0 < n < 1000)
Input
For each case there is a postive number n on base ten, end of file.
Output
For each case output a number on base two.
Sample Input
1
2
3
Sample Output
1
10
11
输出给定数的二进制表示数,还没进制转化那题刺激
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 1e7 + 1;
int n, a[maxn];
void work(int n) {
int cnt = 0;
while (n > 0) {
a[++cnt] = n % 2;
n /= 2;
}
for (int i = cnt; i >= 1; i--)
printf("%d", a[i]);
}
int main() {
while (scanf("%d", &n) != EOF) {
work(n);
printf("\n");
}
return 0;
}
HDU2052 Picture
Problem Description
Give you the width and height of the rectangle,darw it.
Input
Input contains a number of test cases.For each case ,there are two numbers n and m (0 < n,m < 75)indicate the width and height of the rectangle.Iuput ends of EOF.
Output
For each case,you should draw a rectangle with the width and height giving in the input.
after each case, you should a blank line.
Sample Input
3 2
Sample Output
+---+
|......|
|......|
+---+
ps:中间的空格为了排版用了.代替
一道画图题,直接模拟
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
int main() {
while (scanf("%d%d", &n, &m) != EOF) {
for (int i = 1; i <= m + 2; i++) {
for (int j = 1; j <= n + 2; j++) {
if ((i == 1 && j == 1) || (i == 1 && j == n + 2) || (i == m + 2 && j == 1) || (i == m + 2 && j == n + 2))
printf("+");
else if (i == 1 || i == m + 2) printf("-");
else if (j == 1 || j == n + 2) printf("|");
else printf(" ");
}
printf("\n");
}
printf("\n");
}
return 0;
}
HDU2053 Switch Game
Problem Description
There are many lamps in a line. All of them are off at first. A series of operations are carried out on these lamps. On the i-th operation, the lamps whose numbers are the multiple of i change the condition ( on to off and off to on ).
Input
Each test case contains only a number n ( 0< n<= 10^5) in a line.
Output
Output the condition of the n-th lamp after infinity operations ( 0 - off, 1 - on ).
Sample Input
1
5
Sample Output
1
0
Hint:
Consider the second test case:
The initial condition : 0 0 0 0 0 …
After the first operation : 1 1 1 1 1 …
After the second operation : 1 0 1 0 1 …
After the third operation : 1 0 0 0 1 …
After the fourth operation : 1 0 0 1 1 …
After the fifth operation : 1 0 0 1 0 …
The later operations cannot change the condition of the fifth lamp any more. So the answer is 0.
首先先想到直接模拟,好耶!TLE妥妥的
之后就想,第n盏灯的开关状态其实决定于其因数的个数,当其因数的个数为偶数时,它的状态就是关着的
同理,个数为奇数时就是开着的状态
得到代码
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
int main() {
while (scanf("%d", &n) != EOF) {
int cnt = 0;
for (int i = 1; i <= n; i++)
if (n % i == 0) cnt++;
if (cnt % 2 == 0) printf("0\n");
else printf("1\n");
}
return 0;
}
HDU2054 A == B ?
Problem Description
Give you two numbers A and B, if A is equal to B, you should print "YES", or print "NO".
Input
each test case contains two numbers A and B.
Output
for each case, if A is equal to B, you should print "YES", or print "NO".
Sample Input
1 2
2 2
3 3
4 3
Sample Output
NO
YES
YES
NO
给的样例也太坑了吧,拿到题心想“大水题?”,直接写了个简单的判断交上去WA了,然后一脸懵逼
看了题解才知道,还有存在小数点的情况,例如1.000和1是相同的
于是就用制胡窜做吧,如果存在小数点的话先找到小数点,然后去掉后面无效的0,之后再用strcmp()函数对两个制胡窜进行比较
讲解穿插到了代码里,看起来方便些,好多东西都是看着题解现学的...哎
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
char s[100001], a[100001], b[100001];
void change(char s[100001]) {
int len = strlen(s);
int flag = 0, loc;
//寻找是否存在小数点
for (int i = 0; i < len; i++) {
if (s[i] == '.') {
flag = 1;
loc = i; //记录小数点的下标
break;
}
}
//存在小数点
if (flag == 1) {
//把小数点后面无效的零变成字符串结束的标志'\0',所以要倒着
for (int i = len - 1; i > loc; i--) {
if (s[i] == '0') {
s[i] = '\0';
len--;
} else break;
}
//把小数点弄掉
if (s[len - 1] == '.') s[len - 1] = '\0';
}
return;
}
int main() {
while (scanf("%s%s", a, b) != EOF) {
change(a);
change(b);
int num = strcmp(a, b);
if (num == 0) printf("YES\n");
else printf("NO\n");
memset(a, '\0', sizeof(a));
memset(b, '\0', sizeof(b));
}
return 0;
}
HDU2055 An easy problem
Problem Description
we define f(A) = 1, f(a) = -1, f(B) = 2, f(b) = -2, ... f(Z) = 26, f(z) = -26;
Give you a letter x and a number y , you should output the result of y+f(x).
Input
On the first line, contains a number T.then T lines follow, each line is a case.each case contains a letter and a number.
Output
for each case, you should the result of y+f(x) on a line.
Sample Input
6
R 1
P 2
G 3
r 1
p 2
g 3
Sample Output
19
18
10
-17
-14
-4
需要注意的地方就只有:小写字母是负的,大写字母是正的
同时,注意加一个getchar()吞掉换行,一开始没加调了好久都不对......
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
int main() {
while (scanf("%d", &n) != EOF) {
getchar();
while (n--) {
char c;
int y;
scanf ("%c%d", &c, &y);
getchar();
if (c >= 'A' && c <= 'Z') printf("%d\n", y + c - 'A' + 1);
else printf("%d\n", y - (c - 'a' + 1));
}
}
return 0;
}
HDU2056 Rectangles
Problem Description
Given two rectangles and the coordinates of two points on the diagonals of each rectangle,you have to calculate the area of the intersected part of two rectangles. its sides are parallel to OX and OY .
Input
Input The first line of input is 8 positive numbers which indicate the coordinates of four points that must be on each diagonal.The 8 numbers are x1,y1,x2,y2,x3,y3,x4,y4.That means the two points on the first rectangle are(x1,y1),(x2,y2);the other two points on the second rectangle are (x3,y3),(x4,y4).
Output
Output For each case output the area of their intersected part in a single line.accurate up to 2 decimal places.
Sample Input
1.00 1.00 3.00 3.00 2.00 2.00 4.00 4.00
5.00 5.00 13.00 13.00 4.00 4.00 12.50 12.50
Sample Output
1.00
56.25
求两个矩形的相交面积,我们做个图
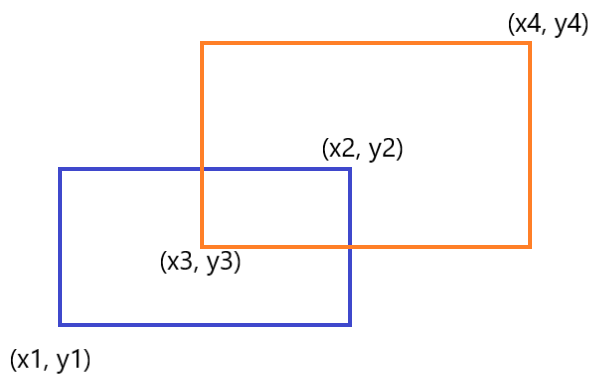
可以得知,相交部分即为(x2-x3)*(y2-y3),我们只需先处理一下输入的长方形,再分别求出相交部分的左下及右上坐标即可
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
double x1, x2, x3, x4, z1, y2, y3, y4;
int main() {
while (scanf("%lf%lf%lf%lf%lf%lf%lf%lf", &x1, &z1, &x2, &y2, &x3, &y3, &x4, &y4) != EOF) {
if (x1 > x2) swap(x1, x2);
if (z1 > y2) swap(z1, y2);
if (x3 > x4) swap(x3, x4);
if (y3 > y4) swap(y3, y4);
x1 = max(x1, x3);
z1 = max(z1, y3);
x2 = min(x2, x4);
y2 = min(y2, y4);
if (x1 > x2 || z1 > y2) printf("0.00\n");
else printf("%.2lf\n", (x2 - x1) * (y2 - z1));
}
return 0;
}
HDU2057 A + B Again
Problem Description
There must be many A + B problems in our HDOJ , now a new one is coming.
Give you two hexadecimal integers , your task is to calculate the sum of them,and print it in hexadecimal too.
Easy ? AC it !
Input
The input contains several test cases, please process to the end of the file.
Each case consists of two hexadecimal integers A and B in a line seperated by a blank.
The length of A and B is less than 15.
Output
For each test case,print the sum of A and B in hexadecimal in one line.
Sample Input
+A -A
+1A 12
1A -9
-1A -12
1A -AA
Sample Output
0
2C
11
-2C
-90
16进制的A+B问题,使用llx输入输出,输出时注意一下负号即可
这里列举出其他形式:
格式字符 格式字符意义
d:以十进制形式输出带符号整数(正数不输出符号)
o:以八进制形式输出无符号整数(不输出前缀O)
x:以十六进制形式输出无符号整数(不输出前缀OX)
u:以十进制形式输出无符号整数
f:以小数形式输出单、双精度实数
e:以指数形式输出单、双精度实数
g:以%f%e中较短的输出宽度输出单、双精度实数
c:输出单个字符
s:输出字符串
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
long long n, m, sum;
int main() {
while (scanf("%llx%llx", &n, &m) != EOF) {
sum = n + m;
if (sum < 0) {
sum = -sum;
printf("-%llX\n", sum);
}
else printf("%llX\n", sum);
}
return 0;
}
HDU2058 The sum problem
Problem Description
Given a sequence 1,2,3,......N, your job is to calculate all the possible sub-sequences that the sum of the sub-sequence is M.
Input
Input contains multiple test cases. each case contains two integers N, M( 1 <= N, M <= 1000000000).input ends with N = M = 0.
Output
For each test case, print all the possible sub-sequence that its sum is M.The format is show in the sample below.print a blank line after each test case.
Sample Input
20 10
50 30
0 0
Sample Output
[1,4]
[10,10]
[4,8]
[6,9]
[9,11]
[30,30]
利用等差数列的性质,末项an=a1+(n-1) * d,n项和Sn=(a1+an) * n/2=a1 * n+n * (n-1) * d/2
在本题中,d=1,Sn=m,即有m=a1 * n+n * (n-1)/2,假设首项是1,我们代入m=a1 * n+n * (n-1)/2,则有n(n+1)=2m,所以项数最多只有sqrt(2m)项
从大到小枚举1~sqrt(2m)的项数,算
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
int main() {
while (scanf("%d%d", &n, &m) != EOF) {
if (n == 0 && m == 0) break;
for (int i = sqrt(2 * m); i >= 1; i--) {
int a = (m - ((i - 1) * i) / 2) / i;
if (m == a * i + (i * (i - 1)) / 2)
cout<< '[' << a << ',' << a + i - 1 << ']' <<endl;
}
cout << endl;
}
return 0;
}
HDU2059 龟兔赛跑
Problem Description
据说在很久很久以前,可怜的兔子经历了人生中最大的打击——赛跑输给乌龟后,心中郁闷,发誓要报仇雪恨,于是躲进了杭州下沙某农业园卧薪尝胆潜心修炼,终于练成了绝技,能够毫不休息得以恒定的速度(VR m/s)一直跑。兔子一直想找机会好好得教训一下乌龟,以雪前耻。
最近正值HDU举办50周年校庆,社会各大名流齐聚下沙,兔子也趁此机会向乌龟发起挑战。虽然乌龟深知获胜希望不大,不过迫于舆论压力,只能接受挑战。
比赛是设在一条笔直的道路上,长度为L米,规则很简单,谁先到达终点谁就算获胜。
无奈乌龟自从上次获胜以后,成了名龟,被一些八卦杂志称为“动物界的刘翔”,广告不断,手头也有了不少积蓄。为了能够再赢兔子,乌龟不惜花下血本买了最先进的武器——“"小飞鸽"牌电动车。这辆车在有电的情况下能够以VT1 m/s的速度“飞驰”,可惜电池容量有限,每次充满电最多只能行驶C米的距离,以后就只能用脚来蹬了,乌龟用脚蹬时的速度为VT2 m/s。更过分的是,乌龟竟然在跑道上修建了很多很多(N个)的供电站,供自己给电动车充电。其中,每次充电需要花费T秒钟的时间。当然,乌龟经过一个充电站的时候可以选择去或不去充电。
比赛马上开始了,兔子和带着充满电的电动车的乌龟并列站在起跑线上。你的任务就是写个程序,判断乌龟用最佳的方案进军时,能不能赢了一直以恒定速度奔跑的兔子。
Input
本题目包含多组测试,请处理到文件结束。每个测试包括四行:
第一行是一个整数L代表跑道的总长度
第二行包含三个整数N,C,T,分别表示充电站的个数,电动车冲满电以后能行驶的距离以及每次充电所需要的时间
第三行也是三个整数VR,VT1,VT2,分别表示兔子跑步的速度,乌龟开电动车的速度,乌龟脚蹬电动车的速度
第四行包含了N(N<=100)个整数p1,p2...pn,分别表示各个充电站离跑道起点的距离,其中0<p1<p2<...<pn<L
其中每个数都在32位整型范围之内。
Output
当乌龟有可能赢的时候输出一行 “What a pity rabbit!"。否则输出一行"Good job,rabbit!";
题目数据保证不会出现乌龟和兔子同时到达的情况。
Sample Input
100
3 20 5
5 8 2
10 40 60
100
3 60 5
5 8 2
10 40 60
Sample Output
Good job,rabbit!
What a pity rabbit!
一开始用的贪心,发现不太对,这题的局部最优解在整体上无法实现最优,看了题解才知道原来是一道动规题
把起点和终点都看作加油站,用一个dp[i]记录到i点时所需要的最少时间,一种情况是从起点直接到这个点,另外的情况时从起点先到j(即dp[j]),再从j到i
那么可能会有个疑问,就是如果到了j点还有余量,再加油会不会有问题呢?其实不会,如果到j你不加油,那肯定是之前的某k点加油了,而那点dp[k]已计算过了,所以不再考虑j点不加油的情况
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int l, n, c, t, vr, vt1, vt2;
double minn, dp[101], time, tt, rt;
int p[101];
int main() {
while (scanf("%d", &l) != EOF) {
scanf("%d%d%d", &n, &c, &t);
scanf("%d%d%d", &vr, &vt1, &vt2);
for (int i = 1; i <= n; i++) cin >> p[i];
p[n + 1] = l;
dp[0] = 0;
for (int i = 1; i <= n + 1; i++) {
minn = 1e9 + 1;
for (int j = 0; j < i; j++) {
int dis = p[i] - p[j];
if (dis <= c) time = dis * 1.0 / vt1;
else time = c * 1.0 / vt1 + (dis - c) * 1.0 / vt2;
if (j != 0) time += t;
time += dp[j];
minn = min(time, minn);
}
dp[i] = minn;
}
tt = dp[n + 1];
rt = l * 1.0 / vr;
if (tt > rt) printf("Good job,rabbit!\n");
else printf("What a pity rabbit!\n");
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号